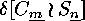 , where
, where 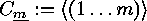 , is just
the centralizer of
, is just
the centralizer of
As an application of this permutation
representation we obtain a description of the centralizers of elements in
finite symmetric groups. To show this we note that 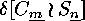 , where
, where 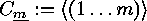 , is just
the centralizer of
, is just
the centralizer of
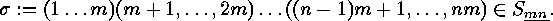
This follows from 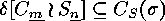 ,
which is clear from
,
which is clear from ![]() together with
together with ![]() and the fact that
and the fact that
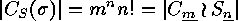 (cf.
(cf. ![]() ).
The general case is now easy:
).
The general case is now easy:
 .
.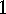 Corollary
If
Corollary
If 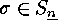 is of type
is of type 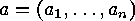 , then
, then
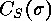 is a subgroup of
is a subgroup of 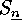 which is similar to the direct
sum
which is similar to the direct
sum

Similarly we can show (recall ![]() )
)
is conjugate to the plethysm 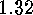 .
.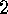 Corollary
The normalizer of the
Corollary
The normalizer of the 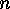 -fold direct sum
-fold direct sum
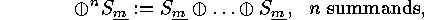

Thus centralizers of elements and normalizers of specific subgroups of symmetric groups turn out to be direct sums of complete monomial groups. Since such groups will also occur as acting groups later on, we also describe their conjugacy classes.