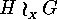, where 
is
a group acting on 
while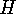 
acts on 
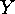. Now we
consider the particular case where is a permutation group, say
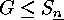, and where we take for 
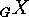the natural action of on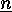 
.
In this case we shorten the notation by putting
A particular case is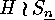 
, the complete monomial group
of degree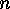 
over 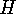. Many important groups are of this form, examples will
be given in a moment. In the case when
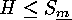, then 
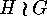has the following natural embedding
into 
:
This can be seen as follows:
Remember the direct factors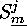 
, for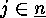 
, of the base
group 
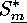of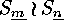 
(cf. the remark on 
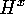in 
). Its image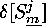 
acts on the block
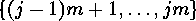as 
does on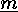 
, while the image 
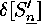of the complement 
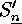of the base group acts on the set of
these 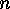subsections 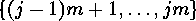of length 
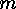of the set 
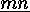as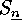 
does act on 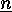. For example the
element
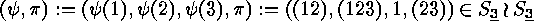
is mapped under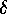 
onto
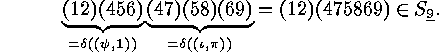
The image of 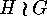under 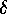will be denoted as follows:
It is called the plethysm
of and 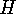, for reasons which will become clear later.
