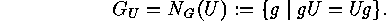The first bunch of examples which illustrate these concepts will show that various important group theoretical structures can be considered as orbits or stabilizers:
.
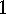Examples
If 
denotes a group, then
acts on itself by left multiplication :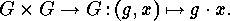 
This action is called the (left)
regular representation
of , it is obviously transitive, and all the
stabilizers are equal to the identity subgroup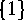 
.
acts on itself by conjugation :
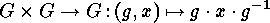. The orbits of this action are the
conjugacy classes
of elements,
and the stabilizers are the
centralizers
of elements:
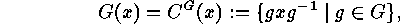
and
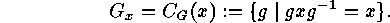
(in short: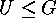 
),
then acts
on the set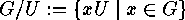 
of its left cosets
as follows:
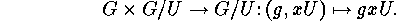
This action is
transitive, and the stabilizer of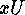 
is the subgroup 
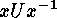which is
conjugate to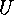 
.
acts on the set 
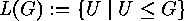of all its subgroups
by conjugation :
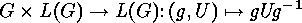. The orbits of this
action are the conjugacy classes of subgroups
, and the stabilizers are the normalizers
:
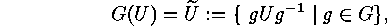
and
