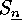 , we show which
of them are in the same conjugacy class, i.e. in the same
orbit of the group
, we show which
of them are in the same conjugacy class, i.e. in the same
orbit of the group 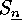 on the set
on the set 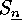 under the
conjugation action (cf.
under the
conjugation action (cf. 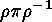 is obtained from the permutation
is obtained from the permutation  :
:
Having described the elements of 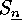 , we show which
of them are in the same conjugacy class, i.e. in the same
orbit of the group
, we show which
of them are in the same conjugacy class, i.e. in the same
orbit of the group 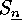 on the set
on the set 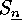 under the
conjugation action (cf.
under the
conjugation action (cf. ![]() ). In order to do this, we first
note how
). In order to do this, we first
note how 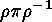 is obtained from the permutation
is obtained from the permutation  :
:
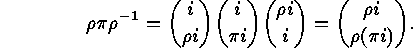
Thus, in terms of cyclic factors of  ,
, 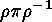 arises from
arises from
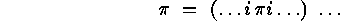
by simply
applying 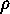 to the points in the cycles of
to the points in the cycles of  :
:
(For any mapping 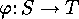 we mean by
we mean by 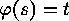 that
that  has to
be replaced by
has to
be replaced by 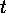 and not that
and not that 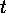 is replaced by
is replaced by 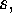 as it is sometimes understood!)
This equation shows that the lengths of the cyclic factors of
as it is sometimes understood!)
This equation shows that the lengths of the cyclic factors of  are the same as those of
are the same as those of 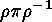 . It is easy to see that,
conversely, for any two elements
. It is easy to see that,
conversely, for any two elements 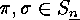 with the same
lengths
with the same
lengths 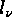 of cyclic factors there exists a
of cyclic factors there exists a 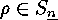 such that
such that 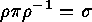 . Hence the lengths of
the cyclic factors of
. Hence the lengths of
the cyclic factors of  characterize its conjugacy class.
To make this more explicit, we introduce the notion of (proper) partition
of
characterize its conjugacy class.
To make this more explicit, we introduce the notion of (proper) partition
of 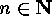 , by which we mean any sequence
, by which we mean any sequence 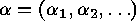 of natural numbers
of natural numbers 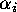 which satisfy
which satisfy
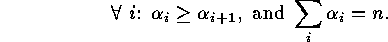
The 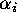 are called the parts
of
are called the parts
of 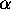 . The fact that
. The fact that 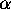 is a partition of
is a partition of 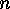 is abbreviated by
is abbreviated by

If 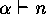 then there exists an
then there exists an 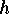 such that
such that 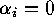 for
all
for
all  . We may therefore write
. We may therefore write

for any such 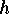 . The minimal
. The minimal 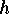 with this property will be denoted
by
with this property will be denoted
by 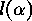 and called the length
of
and called the length
of 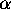 .
The following abbreviation is useful in the case when several
nonzero parts of
.
The following abbreviation is useful in the case when several
nonzero parts of
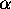 are equal, say
are equal, say 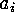 parts are equal to
parts are equal to 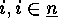 :
:
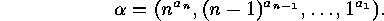
If 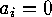 , then
, then 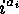 is usually omitted, e.g.
is usually omitted, e.g.
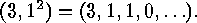 For
For 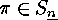 the ordered lengths
the ordered lengths 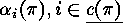 ,
of the cyclic factors of
,
of the cyclic factors of  in cycle notation form a uniquely determined
proper partition
in cycle notation form a uniquely determined
proper partition
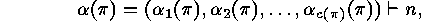
which we call the cycle partition
of  . The corresponding
. The corresponding
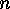 -tuple
-tuple
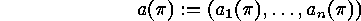
consisting of the multiplicities 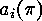 of the parts of length
of the parts of length 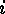 in
in
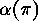 is called the cycle type
of
is called the cycle type
of  . Correspondingly we call an
. Correspondingly we call an 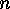 -tuple
-tuple
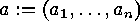 a
cycle type of
a
cycle type of 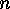 if and only if
each
if and only if
each 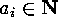 , and
, and
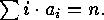 This will be abbreviated by
This will be abbreviated by
