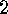The Garsia-Milne bijection




Next: Special symmetry classes
Up: Actions
Previous: The Principle of
In situations where two involutions act we can use the following
result
which allows to replace certain identities of orders by bijections:
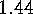 .
. The Garsia-Milne bijection
We assume that
The Garsia-Milne bijection
We assume that
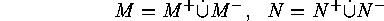
are disjoint decompositions of the finite sets 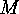 and
and 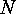 , that
, that
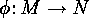 is a sign-preserving bijection, and that
is a sign-preserving bijection, and that 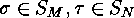 are sign-reversing involutions such that
are sign-reversing involutions such that
 .
Then the following mapping is a bijection:
.
Then the following mapping is a bijection:
where
Proof: Easy checks give the following implications:
and as an immediate consequence, for each natural number 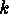 :
:
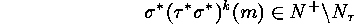
implies that
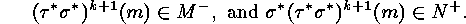
We now prove the existence of 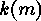 indirectly.
Consider
indirectly.
Consider 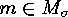 . If
. If 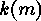 does not exist, then the
implications mentioned above yield that
does not exist, then the
implications mentioned above yield that
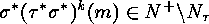 , for each natural
, for each natural 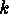 .
But this set is supposed to be finite. Hence there would be
.
But this set is supposed to be finite. Hence there would be
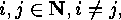 such that
such that 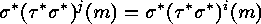 , and thus (assume
, and thus (assume
 ):
): 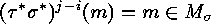 , a contradiction to the
earlier implications since
, a contradiction to the
earlier implications since 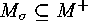 .
.
Finally we mention that
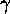 is injective for the following reason:
Assume
is injective for the following reason:
Assume 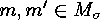 , for which
, for which 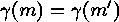 . They satisfy
. They satisfy
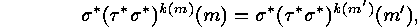
and hence also (assuming 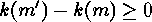 )
)
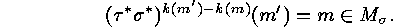
Thus either 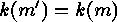 , which is equivalent to
, which is equivalent to 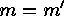 , or there exists a
, or there exists a
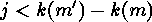 such that
such that
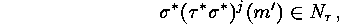
since otherwise we had 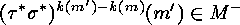 .
This contradicts to the minimality of
.
This contradicts to the minimality of 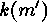 .
.

An application to certain inclusion-exclusion situations runs as follows.
Consider two families 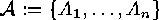 and
and 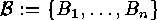 of subsets of two finite sets
of subsets of two finite sets 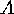 and
and 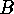 . For each
. For each 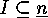 we put
we put
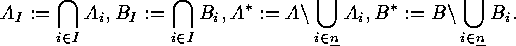
The Principle of Inclusion and Exclusion yields
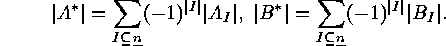
In the case when 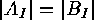 , for each
, for each 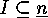 , these two families
, these two families 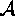 and
and 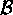 are called
sieve-equivalent ,
a property which implies
are called
sieve-equivalent ,
a property which implies 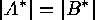 .
.
Now we assume that this holds and that furthermore we are given,
for each 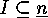 , a bijection
, a bijection

Then the Garsia-Milne construction in fact allows us to sharpen the identity
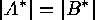 by replacing it by a bijection
by replacing it by a bijection
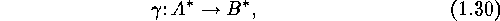
since we need only put
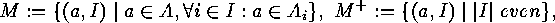
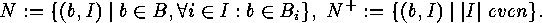
A sign preserving bijection is
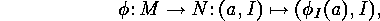
and the involutions 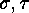 are as
in the proof of the Principle of Inclusion and Exclusion.
Another consequence of the Garsia-Milne bijection is (exercise
are as
in the proof of the Principle of Inclusion and Exclusion.
Another consequence of the Garsia-Milne bijection is (exercise  ):
):
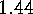 .
.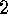 The Two Involutions' Principle If
The Two Involutions' Principle If 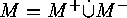 is a disjoint decomposition of the finite set
is a disjoint decomposition of the finite set 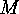 , and
, and
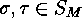 are
sign-reversing involutions such that
are
sign-reversing involutions such that
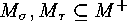 , then each orbit of
, then each orbit of
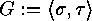 either consists of a fixed point of
either consists of a fixed point of  alone, or it contains exactly one fixed point of
alone, or it contains exactly one fixed point of 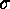 and exactly one fixed
point of
and exactly one fixed
point of  , or it contains neither a fixed point of
, or it contains neither a fixed point of 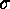 nor a fixed
point of
nor a fixed
point of  . This means in particular that there is a canonical
bijection
between
. This means in particular that there is a canonical
bijection
between 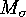 and
and 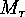 , namely the
, namely the 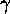 that maps
that maps
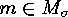 onto the fixed point of
onto the fixed point of  that lies in the orbit
that lies in the orbit
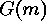 of
of 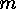 .
.
Exercises
E  .
. Evaluate the derangement number
Evaluate the derangement number
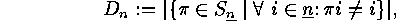
i.e. the number of fixed point free elementes in 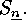 Derive a
recursion for these numbers and show that they
tend to
Derive a
recursion for these numbers and show that they
tend to 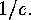
E 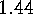 .
.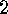 Prove
Prove  .
.




Next: Special symmetry classes
Up: Actions
Previous: The Principle of
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
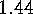 .
. The Garsia-Milne bijection
We assume that
The Garsia-Milne bijection
We assume that
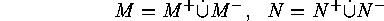
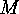 and
and 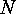 , that
, that
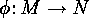 is a sign-preserving bijection, and that
is a sign-preserving bijection, and that 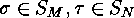 are sign-reversing involutions such that
are sign-reversing involutions such that
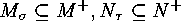 .
Then the following mapping is a bijection:
.
Then the following mapping is a bijection:
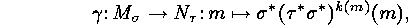
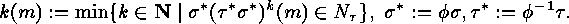
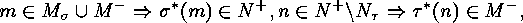
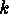 :
:
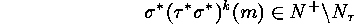
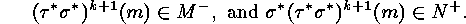
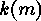 indirectly.
Consider
indirectly.
Consider 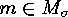 . If
. If 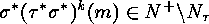 , for each natural
, for each natural 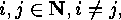 such that
such that 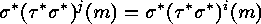 , and thus (assume
, and thus (assume
 ):
): 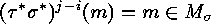 , a contradiction to the
earlier implications since
, a contradiction to the
earlier implications since 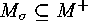 .
.
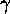 is injective for the following reason:
Assume
is injective for the following reason:
Assume 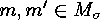 , for which
, for which 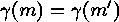 . They satisfy
. They satisfy
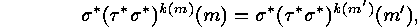
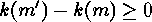 )
)
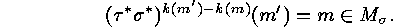
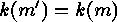 , which is equivalent to
, which is equivalent to 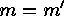 , or there exists a
, or there exists a
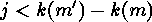 such that
such that
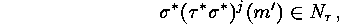
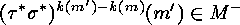 .
This contradicts to the minimality of
.
This contradicts to the minimality of 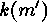 .
.

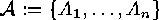 and
and 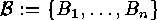 of subsets of two finite sets
of subsets of two finite sets 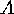 and
and 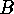 . For each
. For each 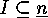 we put
we put
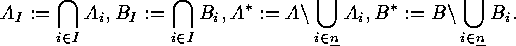
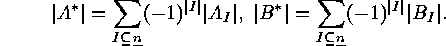
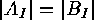 , for each
, for each 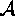 and
and 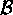 are called
sieve-equivalent
are called
sieve-equivalent 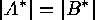 .
.

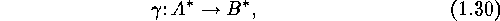
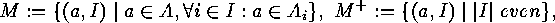
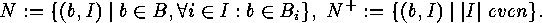
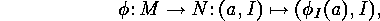
 are as
in the proof of the Principle of Inclusion and Exclusion.
Another consequence of the Garsia-Milne bijection is (exercise
are as
in the proof of the Principle of Inclusion and Exclusion.
Another consequence of the Garsia-Milne bijection is (exercise  .
. The Two Involutions' Principle
The Two Involutions' Principle 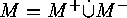 is a disjoint decomposition of the finite set
is a disjoint decomposition of the finite set 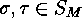 are
sign-reversing involutions such that
are
sign-reversing involutions such that
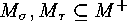 , then each orbit of
, then each orbit of
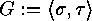 either consists of a fixed point of
either consists of a fixed point of  alone, or it contains exactly one fixed point of
alone, or it contains exactly one fixed point of 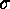 and exactly one fixed
point of
and exactly one fixed
point of  , or it contains neither a fixed point of
, or it contains neither a fixed point of 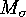 and
and 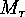 , namely the
, namely the 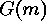 of
of 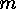 .
. 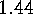 .
.
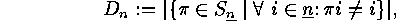
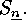 Derive a
recursion for these numbers and show that they
tend to
Derive a
recursion for these numbers and show that they
tend to 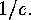
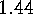 .
.