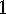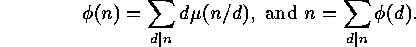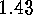 .
.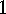 Example Let
Example Let 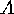 denote a
finite set and let
denote a
finite set and let 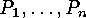 be any given properties. We want to express the number of elements of
be any given properties. We want to express the number of elements of 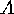 which have none of these properties in terms of numbers of elements which
have some of these properties. In order to do this we indicate by
which have none of these properties in terms of numbers of elements which
have some of these properties. In order to do this we indicate by 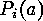 the fact that
the fact that 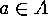 has the property
has the property 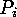 , and for an index set
, and for an index set 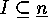 we put
we put
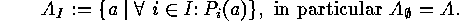
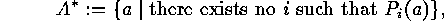
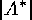 in terms of the
in terms of the 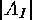 .
The set on which we shall define an involution is
.
The set on which we shall define an involution is
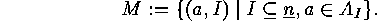
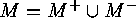 , where
, where
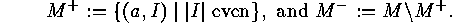
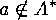 , the number
, the number 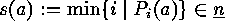 , and define
, and define  on
on 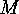 as follows:
as follows:
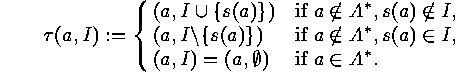
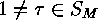 provided that
provided that 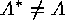 . Furthermore
. Furthermore 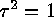 and
and 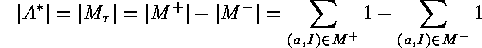
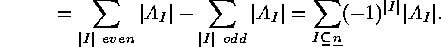
 .
.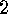 The Principle of Inclusion and Exclusion
The Principle of Inclusion and Exclusion
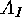 denotes
the set of elements of
denotes
the set of elements of 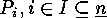 . Then the order of the subset
. Then the order of the subset 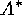 of elements having none of these properties is
of elements having none of these properties is
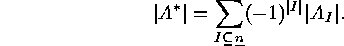
 We would like to express
We would like to express
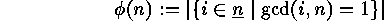
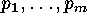 of
of 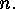 In order to do this we put
In order to do this we put 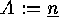 and we define
and we define 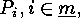 to be the property divisible by
to be the property divisible by 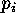 ,
obtaining from the Principle of Inclusion and Exclusion the following
expression for
,
obtaining from the Principle of Inclusion and Exclusion the following
expression for
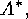 the set of elements of
the set of elements of 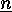 which are relatively prime to
which are relatively prime to 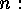
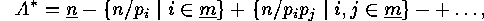
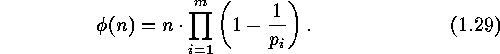

 .
.