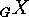 is a finite action, we can apply the
sign map
is a finite action, we can apply the
sign map  to
to 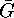 , the permutation group induced by
, the permutation group induced by
 on
on  . Its kernel
. Its kernel
In the case when 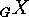 is a finite action, we can apply the
sign map
is a finite action, we can apply the
sign map  to
to 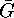 , the permutation group induced by
, the permutation group induced by
 on
on  . Its kernel
. Its kernel
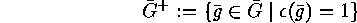
is either 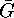 itself or a subgroup of index 2, as is easy to
see. Denoting its inverse image by
itself or a subgroup of index 2, as is easy to
see. Denoting its inverse image by
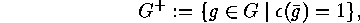
we obtain a useful interpretation of the alternating sum of fixed point numbers:
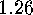 .
.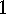 Lemma
For any finite action
Lemma
For any finite action 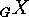 such that
such that 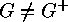 , the number of
orbits of
, the number of
orbits of  on
on  which split over
which split over 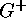 (i.e. which decompose into
more than one - and hence into two -
(i.e. which decompose into
more than one - and hence into two - 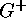 -orbits) is equal to
-orbits) is equal to
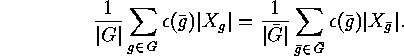
Proof: As 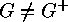 , and hence
, and hence 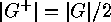 , we have
, we have
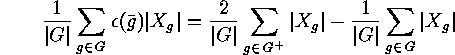
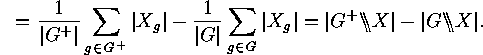
Each orbit of  on
on  is either a
is either a 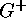 -orbit or it splits into two
orbits of
-orbit or it splits into two
orbits of 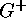 , since
, since 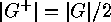 . Hence
. Hence 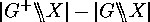 is the number of orbits which split over
is the number of orbits which split over 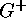 .
Finally the stated identity is obtained by an application of the homomorphism
theorem.
.
Finally the stated identity is obtained by an application of the homomorphism
theorem.

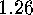 .
.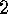 Corollary
In the case when
Corollary
In the case when 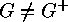 , the number of
, the number of  -orbits on
-orbits on  which
do not split over
which
do not split over 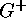 is equal to
is equal to
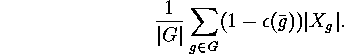
Note what this means. If  acts on a finite set
acts on a finite set  in such a way that
in such a way that
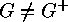 , then we can group the orbits of
, then we can group the orbits of  on
on  into a set
of orbits which are also
into a set
of orbits which are also 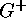 -orbits. In figure
-orbits. In figure ![]() we denote these orbits by the symbol
we denote these orbits by the symbol 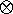 . The other
. The other  -orbits split
into two
-orbits split
into two 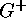 -orbits, we indicate one of them by
-orbits, we indicate one of them by  , the other
one by
, the other
one by  , and call the pair
, and call the pair 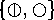 an enantiomeric pair of
an enantiomeric pair of  -orbits.
Hence
-orbits.
Hence ![]() gives
us the number of enantiomeric pairs of orbits, while
gives
us the number of enantiomeric pairs of orbits, while ![]() yields the number of selfenantiomeric
orbits of
yields the number of selfenantiomeric
orbits of  on
on  .
The elements
.
The elements 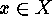 belonging to selfenantiomeric orbits are called
achiral
objects, while the others are
called chiral
.
These notions of
enantiomerism and chirality
are taken from chemistry, where
belonging to selfenantiomeric orbits are called
achiral
objects, while the others are
called chiral
.
These notions of
enantiomerism and chirality
are taken from chemistry, where  is usually the
symmetry group of the molecule while
is usually the
symmetry group of the molecule while 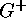 is its subgroup consisting
of the proper rotations. We call
is its subgroup consisting
of the proper rotations. We call 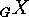 a chiral
action if and only if
a chiral
action if and only if 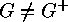 .
.
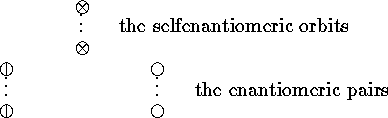
Figure: Enantiomeric pairs and selfenantiomeric orbits
Using this notation we can now rephrase ![]() and
and ![]() in the following way:
in the following way:
while the number of enantiomeric pairs of orbits is
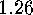 .
.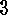 Corollary
If
Corollary
If 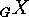 is a finite chiral
action, then the number of
selfenantiomeric orbits of
is a finite chiral
action, then the number of
selfenantiomeric orbits of  on
on  is equal to
is equal to
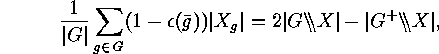
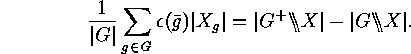
The sign of a cyclic permutation is easy to obtain from the equation
![]() and the homomorphism property of the sign, described in
and the homomorphism property of the sign, described in
![]() :
:
But in fact we need not check the lengths of the cyclic factors of  since
an easy calculation shows (exercise
since
an easy calculation shows (exercise ![]() ) that,
in terms of the number
) that,
in terms of the number 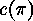 of cyclic factors of
of cyclic factors of  , we have
, we have
Exercises