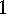Selfcomplementary graphs




Next: Involutions
Up: Actions
Previous: Some congruences
We have evaluated
the number of graphs on  vertices
by examining a certain action of the form
vertices
by examining a certain action of the form 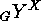 . We shall now give
an example of the form
. We shall now give
an example of the form 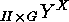 , i.e. a power group action.
Afterwards we shall see how these two examples can be combined in order to
prove an existence theorem for a certain class of graphs. While
doing so we shall meet an interesting and useful counting principle which
uses suitable actions of
, i.e. a power group action.
Afterwards we shall see how these two examples can be combined in order to
prove an existence theorem for a certain class of graphs. While
doing so we shall meet an interesting and useful counting principle which
uses suitable actions of 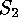 , the smallest nontrivial group.
, the smallest nontrivial group.
Two
labelled graphs 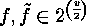 are called complementary
if and only if
are called complementary
if and only if
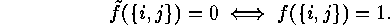

Figure: Two complementary labelled graphs
Correspondingly we say that two graphs, i.e. isomorphism
classes of labelled
ones, are complementary
graphs if and only if one class arises
from the other by
forming the complements. The example of figure  shows that graphs may very well
be selfcomplementary , and hence we ask for the number
of selfcomplementary graphs on
shows that graphs may very well
be selfcomplementary , and hence we ask for the number
of selfcomplementary graphs on  vertices.
In order to prepare the derivation of this number, we notice that the classes
which we obtain by putting a graph and its complement together in one class
are just the orbits of the group
vertices.
In order to prepare the derivation of this number, we notice that the classes
which we obtain by putting a graph and its complement together in one class
are just the orbits of the group 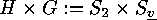 on
the set
on
the set 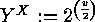 (recall
(recall  ).
According to
).
According to  the number of these orbits is equal to
the number of these orbits is equal to
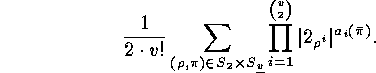
But 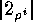 , the number of fixed points of
, the number of fixed points of 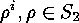 , acting on the set
, acting on the set 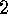 ,
is either 2 or zero. Hence
we separate
the sum over the
,
is either 2 or zero. Hence
we separate
the sum over the 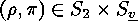 into two sums depending on
into two sums depending on 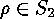 and get the following
expression for the number of these orbits:
and get the following
expression for the number of these orbits:
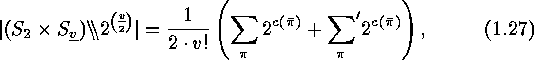
where 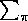 means the sum over all the elements of
means the sum over all the elements of 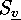 , while
, while
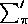 means the sum over all the elements
means the sum over all the elements  of
of 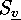 such that
such that
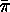 does not contain a cycle of odd length, i.e.
does not contain a cycle of odd length, i.e.
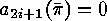 , for each
, for each 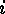 .
There is a program to compute the
number of orbits, which consist of graphs and their
complements.
.
There is a program to compute the
number of orbits, which consist of graphs and their
complements.
In order to derive from this equation
the total number of selfcomplementary graphs on  vertices we use an easy argument which
we have already met when we introduced the
notions of enantiomeric pairs and selfenantiomeric orbits.
A group of order 2 consisting of the identity map and the
complementation acts on the set
of graphs.
This action is chiral if
vertices we use an easy argument which
we have already met when we introduced the
notions of enantiomeric pairs and selfenantiomeric orbits.
A group of order 2 consisting of the identity map and the
complementation acts on the set
of graphs.
This action is chiral if 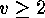 , and
hence the desired number of selfcomplementary graphs is
twice the number given in
, and
hence the desired number of selfcomplementary graphs is
twice the number given in  minus the number in
minus the number in  .
We have obtained
.
We have obtained
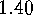 .
.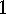 Corollary The number of selfcomplementary
graphs on
Corollary The number of selfcomplementary
graphs on  vertices
is equal to
vertices
is equal to
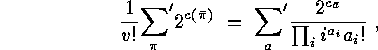
where 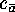 is as in
is as in  , and where
, and where 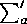 denotes the sum
over all the cycle types
denotes the sum
over all the cycle types  such that for each element
such that for each element  with this
cycle type, the corresponding
with this
cycle type, the corresponding 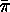 does not contain any cycle of
odd length.
does not contain any cycle of
odd length.
There are some numerical results for
the number of selfcomplementary graphs.
This leads to an existence
theorem (cf. exercise  ):
):
 .
. Theorem Selfcomplementary graphs
on
Theorem Selfcomplementary graphs
on  vertices exist if and only if
vertices exist if and only if  is congruent to 0 or 1 modulo 4.
is congruent to 0 or 1 modulo 4.
Proof:
By corollary  a selfcomplementary graph exists if and only if
there are
a selfcomplementary graph exists if and only if
there are 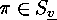 such that
such that 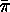 does not
contain any cycle of odd length. Now, if neither
does not
contain any cycle of odd length. Now, if neither 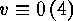 nor
nor
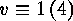 , then
, then 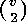 is
odd so that each
is
odd so that each 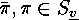 , must
contain a cyclic factor
of odd length. On the other hand,
if
, must
contain a cyclic factor
of odd length. On the other hand,
if 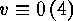 , then to the full cycle
, then to the full cycle  there corresponds a permutation
there corresponds a permutation 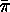 which, by
which, by
 ,
does not contain a cyclic factor of odd length. Finally,
in the case when
,
does not contain a cyclic factor of odd length. Finally,
in the case when 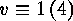 , we consider
, we consider 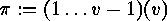 . Again by
. Again by  ,
, 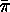 does not contain any cyclic factor of odd length.
does not contain any cyclic factor of odd length.

Exercises
E 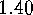 .
. Prove
Prove  directly.
directly.




Next: Involutions
Up: Actions
Previous: Some congruences
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
 vertices
by examining a certain action of the form
vertices
by examining a certain action of the form 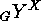 . We shall now give
an example of the form
. We shall now give
an example of the form 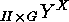 , i.e. a power group action.
Afterwards we shall see how these two examples can be combined in order to
prove an existence theorem for a certain class of graphs. While
doing so we shall meet an interesting and useful counting principle which
uses suitable actions of
, i.e. a power group action.
Afterwards we shall see how these two examples can be combined in order to
prove an existence theorem for a certain class of graphs. While
doing so we shall meet an interesting and useful counting principle which
uses suitable actions of 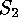 , the smallest nontrivial group.
, the smallest nontrivial group.
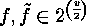 are called complementary
are called complementary 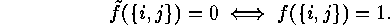

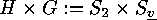 on
the set
on
the set 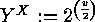 (recall
(recall 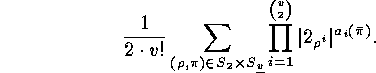
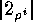 , the number of fixed points of
, the number of fixed points of 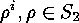 , acting on the set
, acting on the set 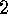 ,
is either 2 or zero. Hence
we separate
the sum over the
,
is either 2 or zero. Hence
we separate
the sum over the 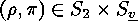 into two sums depending on
into two sums depending on 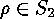 and get the following
expression for the number of these orbits:
and get the following
expression for the number of these orbits:
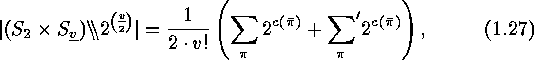
 means the sum over all the elements of
means the sum over all the elements of 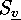 , while
, while
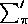 means the sum over all the elements
means the sum over all the elements  of
of 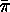 does not contain a cycle of odd length, i.e.
does not contain a cycle of odd length, i.e.
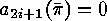 , for each
, for each 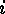 .
There is a program to compute the
.
There is a program to compute the
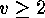 , and
hence the desired number of selfcomplementary graphs is
twice the number given in
, and
hence the desired number of selfcomplementary graphs is
twice the number given in 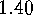 .
. Corollary
Corollary 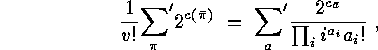
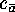 is as in
is as in 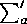 denotes the sum
over all the cycle types
denotes the sum
over all the cycle types  such that for each element
such that for each element 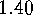 .
.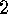 Theorem
Theorem 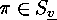 such that
such that 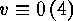 nor
nor
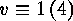 , then
, then 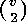 is
odd so that each
is
odd so that each 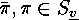 , must
contain a cyclic factor
of odd length. On the other hand,
if
, must
contain a cyclic factor
of odd length. On the other hand,
if  there corresponds a permutation
there corresponds a permutation 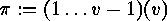 . Again by
. Again by 
 .
.