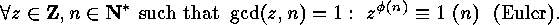According to 
we obtain from the following results:
and also
as well as
.
Corollary
For any subgroups 
and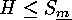 
, the following congruences
hold:
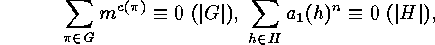
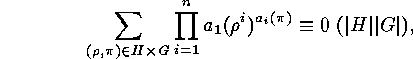
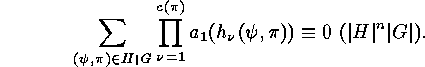
Further congruences show up in the enumeration of group elements with
prescribed properties. This theory of enumeration in finite groups is,
besides the enumeration of chemical graphs, one of the main sources for
the theory of enumeration which we are discussing here. A prominent example
taken from this complex of problems is the following one due to
Frobenius: The number of solutions of the equation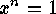 
in a finite
group 
is divisible by 
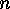, if 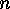divides the order of . There
are many proofs of this result and also many generalizations. Later on we
return to this problem, at present we can only discuss a particular
case which can be treated with the tools we
already have at hand.
.
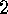Example
Let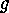 
denote an element of a finite group which forms its own conjugacy
class and consider a prime number 
, which divides 
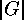. We
want to show that the number of solutions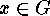 
of the equation
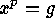is divisible by .
In order to prove this we consider the action of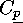 
on the set 
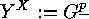. The orbits are of length 1 or .
An orbit is of length 1 if and only if
it consists of a single and therefore of a constant mapping
, say. We now restrict our attention to the following subset
:
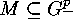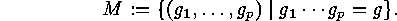
As 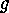forms its own conjugacy class, we obtain a subaction of
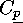on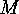 
(for example 
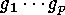is conjugate to 
).
Hence the desired number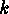 
of solutions of 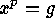is equal to
the number of orbits of length 1 in 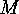. Now we consider the number 
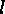of
orbits of length in 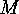. It satisfies the equation
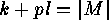. As each equation 
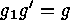has a unique
solutio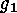n 
in , we moreover have that
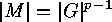. Thus
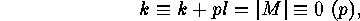
which completes the proof.
We note in passing that the center of consists
of the elements which
form their own conjugacy class, so that we have proved the following:
.
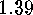Corollary
If the prime divides the order of the
group , then the number of -th roots of each element in the center of
is divisible by .
In particular the number of -th roots of the
unit element 
of has this property (and it is nonzero, since is
a -th root of ), and hence contains elements of
order .
This result can be used in order to give an inductive proof of Sylow's
Theorem which we proved in example .
Exercises
E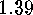 
.
Prove, by considering suitable actions, the following facts:
.
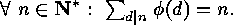
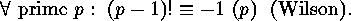
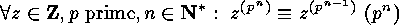