 denote a multiplicative
group and
denote a multiplicative
group and  a nonempty set.
An action
of
a nonempty set.
An action
of  on
on  is described by a mapping
is described by a mapping
Let  denote a multiplicative
group and
denote a multiplicative
group and  a nonempty set.
An action
of
a nonempty set.
An action
of  on
on  is described by a mapping
is described by a mapping
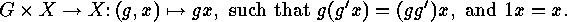
We abbreviate this by saying that  acts
on
acts
on  or simply by calling
or simply by calling
 a
a  - set or by writing
- set or by writing

in short, since  acts from the
left on
acts from the
left on  .
Before
we provide examples, we mention a second but equivalent formulation.
A homomorphism
.
Before
we provide examples, we mention a second but equivalent formulation.
A homomorphism 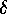 from
from  into the symmetric group
into the symmetric group
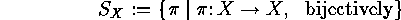
on  is called a permutation
representation of
is called a permutation
representation of  on
on  .
It is easy to check (exercise
.
It is easy to check (exercise ![]() )
that the definition
of action given above is equivalent to
)
that the definition
of action given above is equivalent to
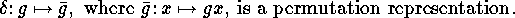
The kernel of 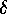 will be
denoted by
will be
denoted by 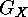 , and so we have, if
, and so we have, if 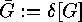 ,
the isomorphism
,
the isomorphism
In the case when 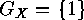 , the action is
said to be faithful.
A very trivial example is the natural action
of
, the action is
said to be faithful.
A very trivial example is the natural action
of 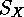 on
on
 itself, where
the corresponding permutation representation
itself, where
the corresponding permutation representation
 is the identity mapping. A number of less trivial examples will follow
in a moment.
is the identity mapping. A number of less trivial examples will follow
in a moment.
Exercises
E  .
. Assume
Assume  to be a
to be a  -set and check carefully that
-set and check carefully that
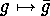 is in fact a permutation representation, i.e. that
is in fact a permutation representation, i.e. that
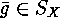 and that
and that 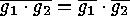 .
.