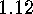 .
.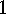 Corollary
If
Corollary
If  denotes a finite group with subgroups
denotes a finite group with subgroups 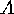 and
and 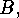 then
then
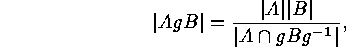
and if 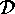 denotes a
transversal of the set
denotes a
transversal of the set 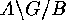 of
of 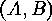 -double cosets, then
-double cosets, then
and if 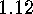 .
. Corollary
If
Corollary
If  denotes a finite group with subgroups
denotes a finite group with subgroups 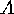 and
and 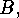 then
then
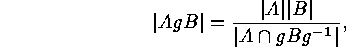
 denotes a
transversal of the set
denotes a
transversal of the set 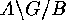 of
of 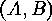 -double cosets, then
-double cosets, then
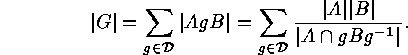
The Cauchy-Frobenius Lemma yields the number of bilateral classes. In order to
evaluate it we have to calculate
the number  of fixed points of
of fixed points of  which is
which is
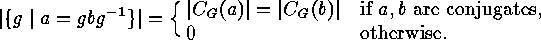
Thus, by the Cauchy-Frobenius Lemma, we obtain
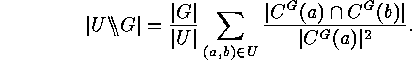
if
of
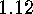 .
. Corollary
If
Corollary
If 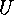 denotes a subgroup of
denotes a subgroup of 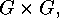
 being a finite group, then the
number of bilateral classes of
being a finite group, then the
number of bilateral classes of  with respect to
with respect to 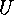 is
is
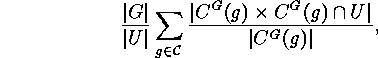
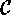 denotes a transversal of the conjugacy classes of elements in
denotes a transversal of the conjugacy classes of elements in 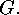 In particular,
the set
In particular,
the set
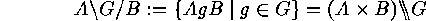
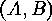 -double cosets has the order
-double cosets has the order
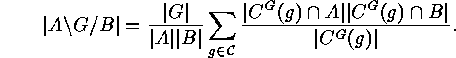
The main reason for the fact that double cosets show up nearly everywhere in
the applications of group actions is the following one (which we immediately
obtain from ![]() ):
):
In particular, a transversal
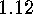 .
. Corollary
If
Corollary
If 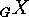 is transitive and
is transitive and 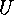 denotes a subgroup
of
denotes a subgroup
of 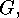 then, for each
then, for each 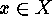 we have the natural bijection
we have the natural bijection
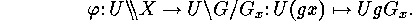
 of the set of double cosets
of the set of double cosets 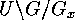 yields the following transversal of the set of orbits of
yields the following transversal of the set of orbits of 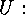
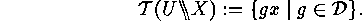
Exercises
E  .
.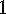 Consider a
Consider a  -set
-set  , a normal subgroup
, a normal subgroup 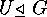 , and the corresponding
restriction
, and the corresponding
restriction 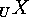 . Check the following facts:
. Check the following facts:
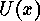 and any
and any 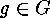 , the set
, the set
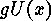 is also an orbit of
is also an orbit of
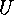 on
on  .
.
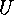 on
on  form a
form a 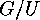 -set, in a natural way.
-set, in a natural way.
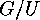 on
on 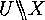 are just the orbits of
are just the orbits of  on
on
 .
.
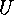 -orbits which belong to the same
-orbits which belong to the same  -orbit are of the same
order.
-orbit are of the same
order.