 which can be derived from
which can be derived from 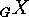 are the
actions of
are the
actions of  on the sets
on the sets
Further actions of  which can be derived from
which can be derived from 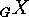 are the
actions of
are the
actions of  on the sets
on the sets
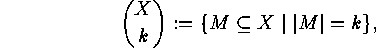
of 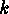 - subsets
of
- subsets
of  ,
, 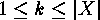 , which are
defined as follows:
, which are
defined as follows:
The action 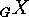 is called
is called 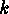 - homogeneous if and only
if the corresponding
action of
- homogeneous if and only
if the corresponding
action of  on
on 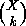 is transitive. An obvious example is the natural
action of
is transitive. An obvious example is the natural
action of 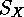 on
on  , it is
, it is 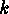 -homogeneous for
-homogeneous for 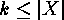 .
.