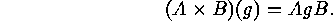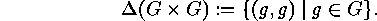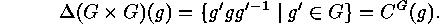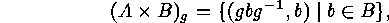Bilateral classes, symmetry classes of mappings




Next: Double Cosets
Up: Actions
Previous: Similar Actions
From a given action we can
derive various other actions in a natural
way, e.g. 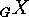 yields
yields 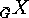 ,
, 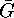 being the
homomorphic image of
being the
homomorphic image of  in
in 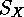 , which was already mentioned. We also
obtain the subactions
, which was already mentioned. We also
obtain the subactions
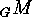 on subsets
on subsets 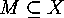 which
are nonempty unions of orbits. Furthermore there are the restrictions
which
are nonempty unions of orbits. Furthermore there are the restrictions
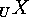 to the subgroups
to the subgroups 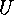 of
of  . As the orbits of
. As the orbits of 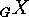 are unions
of orbits of
are unions
of orbits of 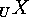 , the comparison of actions and restrictions is a
suitable way of generalizing or specializing structures if they can be
defined as orbits. The following example will show what is meant by this.
, the comparison of actions and restrictions is a
suitable way of generalizing or specializing structures if they can be
defined as orbits. The following example will show what is meant by this.
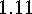 .
. Example
Let
Example
Let 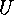 denote a subgroup of the direct product
denote a subgroup of the direct product
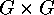 . Then U acts on
. Then U acts on  as follows:
as follows:
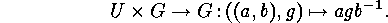
The orbits 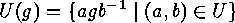 of this action are called
the bilateral classes
of
of this action are called
the bilateral classes
of  with respect to
with respect to 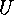 . By specializing
. By specializing
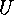 we obtain various interesting group theoretical structures some of
which have been mentioned already:
we obtain various interesting group theoretical structures some of
which have been mentioned already:

Hence left and right cosets, double cosets and conjugacy classes turn out to
be special cases of bilateral classes. Being orbits, two of them are either equal or
disjoint, moreover, their order is the index of the stabilizer of an element.
We have mentioned this in connection with conjugacy classes and centralizers
of elements, here is the consequence for double cosets: Since
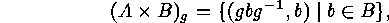
we obtain




Next: Double Cosets
Up: Actions
Previous: Similar Actions
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
 yields
yields 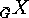 ,
, 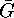 being the
homomorphic image of
being the
homomorphic image of  in
in 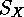 , which was already mentioned. We also
obtain the subactions
, which was already mentioned. We also
obtain the subactions
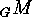 on subsets
on subsets 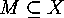 which
are nonempty unions of orbits. Furthermore there are the restrictions
which
are nonempty unions of orbits. Furthermore there are the restrictions
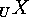 to the subgroups
to the subgroups 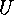 of
of  . As the orbits of
. As the orbits of 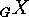 are unions
of orbits of
are unions
of orbits of 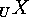 , the comparison of actions and restrictions is a
suitable way of generalizing or specializing structures if they can be
defined as orbits. The following example will show what is meant by this.
, the comparison of actions and restrictions is a
suitable way of generalizing or specializing structures if they can be
defined as orbits. The following example will show what is meant by this.
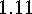 .
. Example
Example 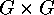 . Then U acts on
. Then U acts on 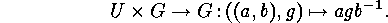
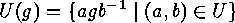 of this action are called
the bilateral classes
of this action are called
the bilateral classes  is a subgroup of
is a subgroup of  and
and 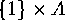 are subgroups of
are subgroups of 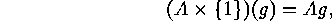
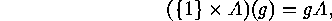
 denotes a second subgroup
of
denotes a second subgroup
of 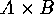 ,
obtaining as orbits
the
,
obtaining as orbits
the
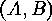 - double cosets
- double cosets