Chirality: Enantiopure compound
|
To understand this, let us assume to have synthesized the compound in question via stereoselective synthesis starting with an achiral precursor. Then the enantiomer ratio is
where If the compond sample at issue was obtained by separation of a racemate or by further enrichment of an already nonracemic sample, e.g. by chromatography on a "chiral column", then quite analogous considerations apply to the separation process. The important energy then is the difference of the free enthalpies of adsorption of the enantiomers at the chiral column material, both finite quantities, so that again their difference cannot be infinite. Analogous considerations are valid not only for enantiopurity but even for chemical purity of a compound sample. The ratio of substance to impurity always exponentially depends on the difference of two finite energies, so that it can never be infinite. From this it follows: A completely pure compound sample does not exist. And this is not the consequence of some missing accuracy of measurement, but the consequence of a fundamental principle. |




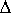
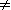 / RT) =
exp((
/ RT) =
exp((