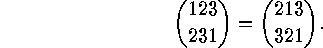
The points which form the first row need not be written in their natural order, e.g.
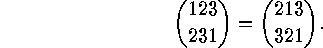
Keeping this in mind, we call a permutation 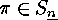 a cyclic
permutation or a cycle if and only if it can be written
in the form
a cyclic
permutation or a cycle if and only if it can be written
in the form
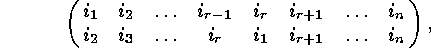
where 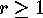 .
In order to emphasize
.
In order to emphasize  we also call it an r-cycle .
We note that in this case the orbits of the subgroup generated by
this permutation are the following
subsets of
we also call it an r-cycle .
We note that in this case the orbits of the subgroup generated by
this permutation are the following
subsets of 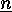 :
: 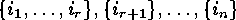 .
We therefore abbreviate
this cycle by
.
We therefore abbreviate
this cycle by 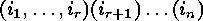 ,
where the points which are cyclically permuted are put together in
round brackets. For example
,
where the points which are cyclically permuted are put together in
round brackets. For example 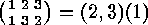 . Commas which seperate the points may be omitted if no confusion
can arise (e.g if
. Commas which seperate the points may be omitted if no confusion
can arise (e.g if  ), and 1-cycles can be left out if it is clear
which
), and 1-cycles can be left out if it is clear
which 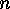 is meant. Hence we can write
is meant. Hence we can write 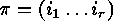 for the
for the
 -cycle introduced above. This cycle
-cycle introduced above. This cycle  can also be expressed in
terms of
can also be expressed in
terms of 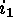 alone:
alone: 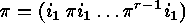 . Using all these
abbreviations and denoting by
. Using all these
abbreviations and denoting by 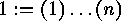 the identity element,
we obtain for example
the identity element,
we obtain for example
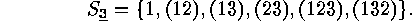
There are the elements of the
symmetric group 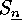 in cycle notation.
The notation for a cyclic permutation is not uniquely determined, since
in cycle notation.
The notation for a cyclic permutation is not uniquely determined, since
2-cycles are called transpositions .
The order
of a cycle
 , i.e. the order of the cyclic group
, i.e. the order of the cyclic group  generated by this cycle, is equal to its length
:
generated by this cycle, is equal to its length
:
Two cycles  and
and 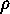 are called disjoint ,
if the two sets
of points which are not fixed by
are called disjoint ,
if the two sets
of points which are not fixed by  and
and 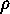 are disjoint sets.
Notice that, for example,
are disjoint sets.
Notice that, for example, 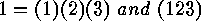 are disjoint cycles.
Disjoint cycles
are disjoint cycles.
Disjoint cycles  and
and 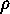 commute, i.e.
commute, i.e. 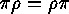 .
(We read compositions of mappings from right to left, so that
.
(We read compositions of mappings from right to left, so that
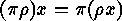 .) Each permutation of a
finite set can be
written as a product of pairwise different disjoint cycles, e.g.
.) Each permutation of a
finite set can be
written as a product of pairwise different disjoint cycles, e.g.
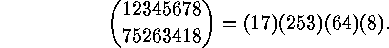
There are some more examples for the cycle decomposition of a permutation.
The disjoint cyclic factors 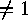 of
of 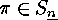 are
uniquely determined by
are
uniquely determined by  and therefore we call these factors together
with the
fixed point
cycles of
and therefore we call these factors together
with the
fixed point
cycles of  the cyclic factors
of
the cyclic factors
of  .
Let
.
Let 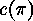 denote the number of these cyclic factors of
denote the number of these cyclic factors of  (including 1-cycles), let
(including 1-cycles), let 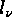 be their lengths,
be their lengths, 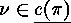 (recall that
(recall that 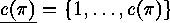 ),
choose, for each
),
choose, for each  an element
an element 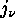 of the
of the  -th cyclic
factor. Then
-th cyclic
factor. Then
This notation becomes uniquely determined if we choose the 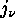 so
that
so
that
If this holds, then ![]() is called the (standard) cycle notation
for
is called the (standard) cycle notation
for  . We note in passing that the sets
. We note in passing that the sets 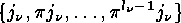 of points which
are cyclically permuted by
of points which
are cyclically permuted by  are just the orbits of the cyclic group
are just the orbits of the cyclic group 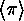 generated
by
generated
by  .
.