Similar Actions




Next: Bilateral classessymmetry
Up: Actions
Previous: The Cauchy-Frobenius Lemma
Under enumerative aspects 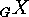 is essentially the same as
is essentially the same as 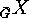 .
This leads to the question of a suitable concept of
morphism between actions of groups.
To begin with, two actions will be
called isomorphic
iff they differ only by an isomorphism
.
This leads to the question of a suitable concept of
morphism between actions of groups.
To begin with, two actions will be
called isomorphic
iff they differ only by an isomorphism
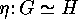 of the groups and a bijection
of the groups and a bijection 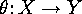 between the sets which satisfy
between the sets which satisfy
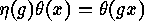 .
In this case we shall write
.
In this case we shall write

in order to indicate the existence of such a pair of mappings. If
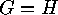 we call
we call 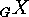 and
and 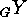 similar actions,
if and only if they are isomorphic by
similar actions,
if and only if they are isomorphic by
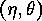 , where moreover
, where moreover 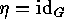 , the identity mapping (cf.
exercise
, the identity mapping (cf.
exercise  ). We indicate this by
). We indicate this by

An important
special case
follows directly from the proof of  :
:
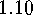 .
. Lemma
If
Lemma
If 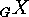 is transitive then, for any
is transitive then, for any 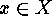 ,
we have that
,
we have that
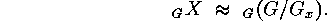
A weaker concept is that of  - homomorphy.
We shall write
- homomorphy.
We shall write

if and only if there exists a mapping 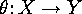 which is
compatible with the action of
which is
compatible with the action of 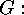
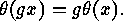 Later on we shall see
that the use of
Later on we shall see
that the use of  -homomorphisms is one of the most important tools in the
constructive theory of discrete structures which can be defined as orbits of
groups on finite sets. A characterization of
-homomorphisms is one of the most important tools in the
constructive theory of discrete structures which can be defined as orbits of
groups on finite sets. A characterization of  -homomorphy gives
-homomorphy gives
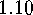 .
.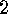 Lemma
Two actions
Lemma
Two actions 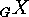 and
and 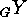 are
are  -homomorphic if and
only if for each
-homomorphic if and
only if for each 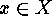 there exist
there exist 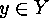 such that
such that 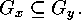
Proof: In the case when 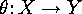 is a
is a  -homomorphism, then
-homomorphism, then
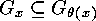 since, for each
since, for each 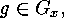
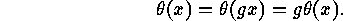
On the other hand, if for each 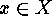 there exist
there exist 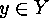 such that
such that 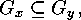 we can construct a
we can construct a  -homomorphism in the following way:
Assume a transversal
-homomorphism in the following way:
Assume a transversal 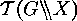 of the orbits, and choose, for each
element
of the orbits, and choose, for each
element 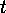 of this transversal, an element
of this transversal, an element 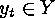 such that
such that 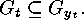 An easy check shows that
An easy check shows that
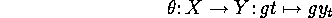
is a well defined mapping and also a  -homomorphism.
-homomorphism.

Exercises
E 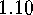 .
. Check that the
Check that the  -isomorphy
-isomorphy 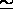 (and hence also the
(and hence also the
 -similarity
-similarity 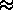 ) is an equivalence relation on group actions.
) is an equivalence relation on group actions.
E 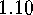 .
. Consider the following definition: We call actions
Consider the following definition: We call actions 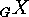 and
and 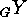 inner isomorphic
if and only if there exists a pair
inner isomorphic
if and only if there exists a pair 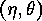 such that
such that
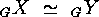 and where
and where 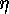 is an inner automorphism
, which means that
is an inner automorphism
, which means that
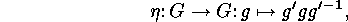
for a suitable 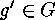 . Show that this equivalence relation has the same
classes as
. Show that this equivalence relation has the same
classes as 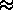 .
.




Next: Bilateral classessymmetry
Up: Actions
Previous: The Cauchy-Frobenius Lemma
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
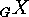 is essentially the same as
is essentially the same as 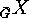 .
This leads to the question of a suitable concept of
morphism between actions of groups.
To begin with, two actions will be
called isomorphic
iff they differ only by an isomorphism
.
This leads to the question of a suitable concept of
morphism between actions of groups.
To begin with, two actions will be
called isomorphic
iff they differ only by an isomorphism
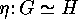 of the groups and a bijection
of the groups and a bijection 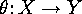 between the sets which satisfy
between the sets which satisfy
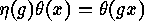 .
In this case we shall write
.
In this case we shall write

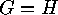 we call
we call 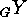 similar actions,
similar actions, 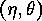 , where moreover
, where moreover 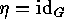 , the identity mapping (cf.
exercise
, the identity mapping (cf.
exercise 
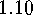 .
. Lemma
Lemma 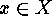 ,
we have that
,
we have that
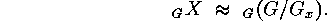
 - homomorphy.
We shall write
- homomorphy.
We shall write

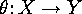 which is
compatible with the action of
which is
compatible with the action of 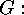
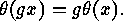 Later on we shall see
that the use of
Later on we shall see
that the use of 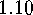 .
.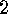 Lemma
Lemma 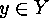 such that
such that 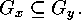
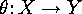 is a
is a 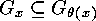 since, for each
since, for each 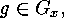
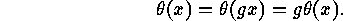
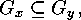 we can construct a
we can construct a 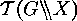 of the orbits, and choose, for each
element
of the orbits, and choose, for each
element 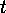 of this transversal, an element
of this transversal, an element 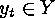 such that
such that 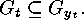 An easy check shows that
An easy check shows that
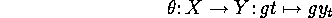

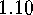 .
.
 (and hence also the
(and hence also the
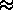 ) is an equivalence relation on group actions.
) is an equivalence relation on group actions.
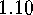 .
.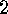
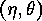 such that
such that
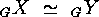 and where
and where 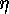 is an inner automorphism
is an inner automorphism
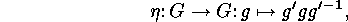
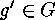 . Show that this equivalence relation has the same
classes as
. Show that this equivalence relation has the same
classes as