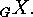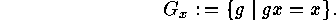
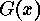 , which are subsets of
, which are subsets of  , there correspond
certain subgroups of
, there correspond
certain subgroups of  . For each
. For each 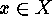 we introduce its
stabilizer :
we introduce its
stabilizer :
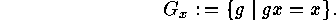
This is the subgroup of elements of  that stabilize the point
that stabilize the point 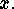 There is
also the subgroup of elements which pointwise stabilize the elements of
a subset
There is
also the subgroup of elements which pointwise stabilize the elements of
a subset 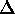 of
of 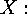
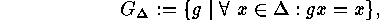
and which is called the pointwise stabilizer
of 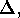 in contrast to the setwise stabilizer
of
in contrast to the setwise stabilizer
of 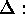
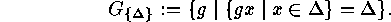
We note in passing that 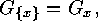 that
that 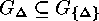 and that this notation is compatible
with the notation
and that this notation is compatible
with the notation 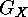 for the kernel of the permutation representation
for the kernel of the permutation representation
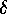 corresponding to
corresponding to