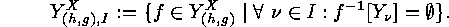
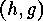 we use the preceeding corollaries
together with an application of the Principle of Inclusion and
Exclusion in order to get rid of the nonsurjective fixed points. We denote
by
we use the preceeding corollaries
together with an application of the Principle of Inclusion and
Exclusion in order to get rid of the nonsurjective fixed points. We denote
by 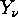 the set of points
the set of points 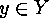 contained in the
contained in the  -th cyclic
factor of
-th cyclic
factor of 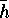 and put, for each index set
and put, for each index set 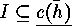 :
:
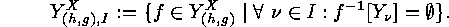
Then, by the Principle of Inclusion and Exclusion, we obtain for the
desired number of surjective fixed points of 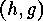 the following expression:
the following expression:
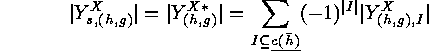
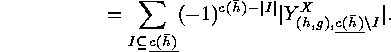
Now we recall that
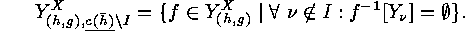
This set can be identified with 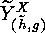 , where
, where 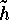 denotes the product of the cyclic factors of
denotes the product of the cyclic factors of 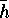 the numbers of
which lie in
the numbers of
which lie in 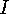 , and where
, and where 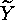 is the set of points contained in
these cyclic factors. Thus
is the set of points contained in
these cyclic factors. Thus
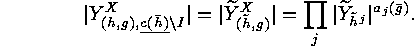
We can make this more explicit by an application of ![]() which yields:
which yields:
Putting these things together we conclude
where the middle sum is taken over all
the sequences
and
where the sum is taken over all the sequences 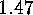 .
. Corollary The number of surjective fixed points of
Corollary The number of surjective fixed points of 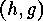 is
is
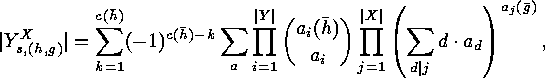
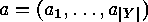 of
natural numbers
of
natural numbers 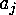 such that
such that 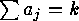 (they correspond to all possible choices of
(they correspond to all possible choices of 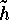 out of
out of 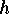 , where
, where
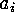 of the chosen cyclic factors of
of the chosen cyclic factors of 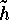 are
are 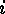 -cycles).
Hence the numbers of surjective fixed points of
-cycles).
Hence the numbers of surjective fixed points of 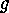 and of
and of 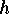 amount to:
amount to:
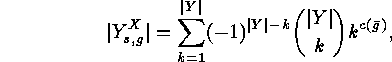
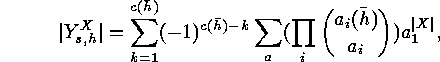
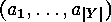 ,
,
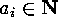 and
and 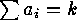 .
.
An application of the Cauchy-Frobenius Lemma finally yields the desired numbers of surjective symmetry classes:
where the inner sum is taken over the sequences
and
where the last sum is to be
taken over all the sequences 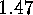 .
. Theorem The number
Theorem The number
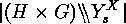 of surjective
of surjective 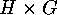 -classes is
-classes is
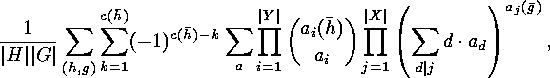
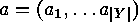 described in the corollary above. This implies, by
restriction, the equations
described in the corollary above. This implies, by
restriction, the equations
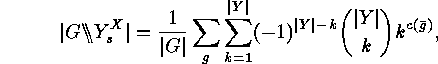
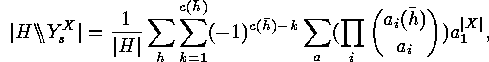
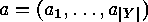 such that
such that 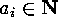 and
and 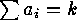 .
.
Try to compute the number of surjective symmetry classes for various group actions.
Exercises