Paradigmatic Examples 2




Next: Finite symmetric groups
Up: Actions
Previous: Paradigmatic Examples
 .
. Lemma
In each case when a direct product
Lemma
In each case when a direct product 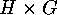 acts on a set
acts on a set 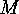 ,
we obtain both a natural action of
,
we obtain both a natural action of 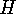 on the set of orbits of
on the set of orbits of  :
:
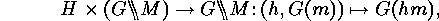
and a natural action of  on the set of orbits of
on the set of orbits of 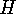 :
:
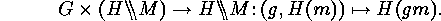
Moreover the orbit of 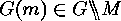 under
under 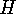 is the set consisting of
the orbits of
is the set consisting of
the orbits of  on
on 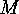 that form
that form 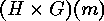 , while the orbit of
, while the orbit of
 under
under  is the set consisting of the orbits of
is the set consisting of the orbits of
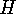 on
on 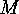 that form
that form 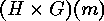 , and therefore the following
identity holds:
, and therefore the following
identity holds:
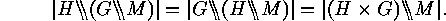
In particular each action of the form
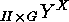 can be considered as an action of
can be considered as an action of 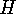 on
on 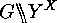 or
as an action of
or
as an action of  on
on 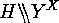 .
.
The corresponding result on wreath products is due to W. Lehmann, and it
reads as follows:
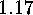 .
. Lemma
The following mapping is a bijection:
Lemma
The following mapping is a bijection:
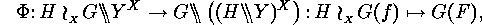
if 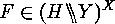 is defined by
is defined by 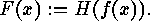 In particular,
In particular,
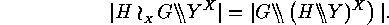
Proof: It is easy to see that  is well defined.
In order to prove that
is well defined.
In order to prove that 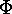 is injective assume
is injective assume
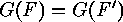 , so that there exist
, so that there exist
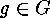 such that
such that 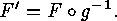 But this implies
But this implies
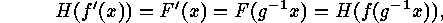
for each 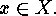 Therefore there must exist, for each
Therefore there must exist, for each 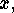
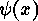 such that
such that 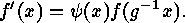 Summing up there exist
Summing up there exist
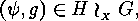 for which
for which 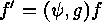 , and so
, and so
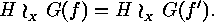
In order to show that 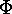 is surjective assume that
is surjective assume that
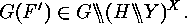 Defining
Defining 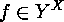 in such a way that
in such a way that
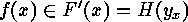 , say
, say 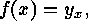 for all
for all 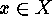 , then, for
, then, for 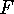 defined as above,
defined as above,
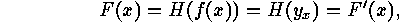
which gives
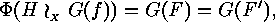 and it completes the proof.
and it completes the proof.

Exercises
E  .
. Check lemma
Check lemma  .
.
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
 .
.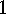 Lemma
In each case when a direct product
Lemma
In each case when a direct product 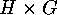 acts on a set
acts on a set 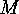 ,
we obtain both a natural action of
,
we obtain both a natural action of 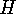 on the set of orbits of
on the set of orbits of  :
:
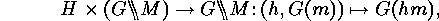
 on the set of orbits of
on the set of orbits of 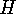 :
:
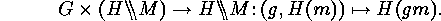
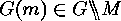 under
under 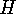 is the set consisting of
the orbits of
is the set consisting of
the orbits of  on
on 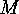 that form
that form 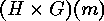 , while the orbit of
, while the orbit of
 under
under  is the set consisting of the orbits of
is the set consisting of the orbits of
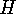 on
on 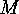 that form
that form 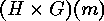 , and therefore the following
identity holds:
, and therefore the following
identity holds:
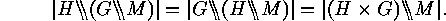
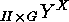 can be considered as an action of
can be considered as an action of 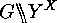 or
as an action of
or
as an action of 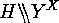 .
.
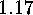 .
. Lemma
Lemma 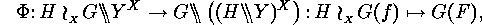
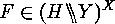 is defined by
is defined by 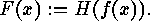 In particular,
In particular,
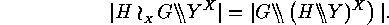
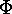 is well defined.
In order to prove that
is well defined.
In order to prove that 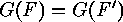 , so that there exist
, so that there exist
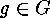 such that
such that 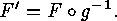 But this implies
But this implies
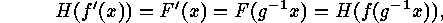
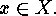 Therefore there must exist, for each
Therefore there must exist, for each 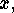
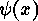 such that
such that 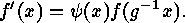 Summing up there exist
Summing up there exist
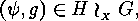 for which
for which 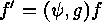 , and so
, and so
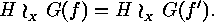
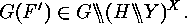 Defining
Defining 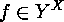 in such a way that
in such a way that
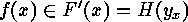 , say
, say 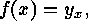 for all
for all 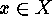 , then, for
, then, for 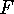 defined as above,
defined as above,
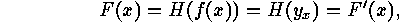
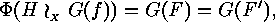 and it completes the proof.
and it completes the proof.

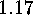 .
.