Next: References Up: Algorithms for Group Actions Previous: Basic Principles
![]()
![]()
![]()
Next: References Up: Algorithms for Group Actions Previous: Basic Principles
The new generator relies on a strategy of determining first how all graphs with a given degree partition can be built up recursively from regular graphs. The basic result for this approach is the following.
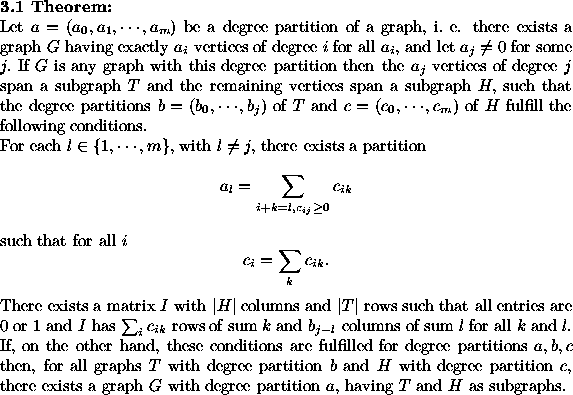
There are well known criteria for a degree partition to be the degree partition of a graph [H]. Also, the existence condition for a 0/1-matrix with the required row and column sums can be expressed numerically without any explicit construction by the Gale-Ryser theorem, see[vLW] pp. 148-149. Thus, one can decide in advance whether a splitting of a given degree sequence a into two degree sequences b and c of graphs, will permit the construction of a graph G with the required degree sequence a from two corresponding graphs T and H.
It is also clear that the subgraphs T and H in such a case are uniquely determined in any resulting graph G. Also the incidence structure matrix I having a row for each vertex ![]() and a column for each vertex
and a column for each vertex ![]() in which an edge connecting x to y is denoted by the entry 1 in the corresponding place of I, is unique. We use this decomposition of G to define homomorphisms of group actions. We consider
in which an edge connecting x to y is denoted by the entry 1 in the corresponding place of I, is unique. We use this decomposition of G to define homomorphisms of group actions. We consider ![]() as the set of vertices of the graphs with degree partition a, such that
as the set of vertices of the graphs with degree partition a, such that ![]() The symmetric group
The symmetric group ![]() acts on the set of all labelled graphs with vertex set V and degree partition a, such that the isomorphism types of graphs are just the orbits of
acts on the set of all labelled graphs with vertex set V and degree partition a, such that the isomorphism types of graphs are just the orbits of ![]() on this set. Mapping each graph G onto the set partition
on this set. Mapping each graph G onto the set partition ![]() where
where ![]() is the set of vertices of degree i of G, gives a first simplifying homomorphism of the action of
is the set of vertices of degree i of G, gives a first simplifying homomorphism of the action of ![]() Here, of course, all graphs with degree partition a and vertex set V are mapped onto a set partition with
Here, of course, all graphs with degree partition a and vertex set V are mapped onto a set partition with ![]() for each i. Therefore
for each i. Therefore ![]() is transitive on all these set partitions. The split version of the use
of homomorphisms then tells us that we only need to look for graphs with
is transitive on all these set partitions. The split version of the use
of homomorphisms then tells us that we only need to look for graphs with ![]() , for each i, and the action of the Young subgroup Y, which is the intersection of the normalizers of all such
, for each i, and the action of the Young subgroup Y, which is the intersection of the normalizers of all such ![]() Now we choose a fixed index j as in theorem 3.1. We restrict the action of Y simultaneously to the subgraphs spanned by
Now we choose a fixed index j as in theorem 3.1. We restrict the action of Y simultaneously to the subgraphs spanned by ![]() to the subgraphs spanned by the remaining vertices, and to the action on
the incidence structures I intertwining the two subgraphs. This is again a homomorphism of group actions
of Y. So, the split version applies also to this situation. Thus, we may first
find all degree sequences b and c and, having constructed the corresponding graphs T and H up to equivalence under Y, find the possible incidence structures I up to equivalence under
to the subgraphs spanned by the remaining vertices, and to the action on
the incidence structures I intertwining the two subgraphs. This is again a homomorphism of group actions
of Y. So, the split version applies also to this situation. Thus, we may first
find all degree sequences b and c and, having constructed the corresponding graphs T and H up to equivalence under Y, find the possible incidence structures I up to equivalence under ![]() and in a last step form the required graphs G.
and in a last step form the required graphs G.
The strategy obviously can be applied recursively to the construction of the graphs T and H, as long as the respective degree partitions consist of more than one non-zero entry. This reduces the construction problem from simple graphs with prescribed degree sequence to that of regular graphs and the problem of how to paste the subgraphs T and H together. Regular graphs are constructed by an implementation [M] of G. Brinkmann's method [Br]. This is the fastest method known to us presently. The problem of pasting T and H together breaks into two main steps.
Suppose H has ![]() vertices of degree i and
vertices of degree i and ![]() of them have just k neighbors in T. Then we have to find all partitions of the set of the
of them have just k neighbors in T. Then we have to find all partitions of the set of the ![]() vertices into these subsets of
vertices into these subsets of ![]() subsets for all k up to equivalence under the automorphism group of H. This can be done by orderly generation or, better, by a combination of
homomorphism steps and orderly generation. It is important to notice that
we will often find only a few different isomorphism types of orbit problems
in this step. Moreover, since very often the automorphism group of H will be trivial or act trivially on this set of partitions, the solutions
of one case may be implicitly carried over to all the isomorphic cases by
just noting which bijections must be applied. Also, all subgraphs H with the same edge degree sequence and trivial automorphism group can be
considered, essentially, only one case.
subsets for all k up to equivalence under the automorphism group of H. This can be done by orderly generation or, better, by a combination of
homomorphism steps and orderly generation. It is important to notice that
we will often find only a few different isomorphism types of orbit problems
in this step. Moreover, since very often the automorphism group of H will be trivial or act trivially on this set of partitions, the solutions
of one case may be implicitly carried over to all the isomorphic cases by
just noting which bijections must be applied. Also, all subgraphs H with the same edge degree sequence and trivial automorphism group can be
considered, essentially, only one case.
Now we know the number of entries 1 in each row and each column of I. We have to find a set of representatives of the different ways to fill this matrix, up to the action of the two automorphism groups Aut H and Aut T on the sets of rows and columns, respectively. We can first partition I into blocks where the corresponding vertices of each row and those of each column are in the same orbit of the automorphism group of T or the stabilizer of the selected partition in the automorphism group of H. Then we have to assign to these blocks a number of 1's that we want to distribute there. We end up with the problem of selecting from the set of places in the block the subsets of those which should get an entry 1. This can be done by orderly generation. By the homomorphism principle, only the stabilizer of any such solution has to be considered in its action on the next block to fill. We may even split that block further into the orbits of that stabilizer. Thus, again the acting groups and the blocks become smaller by some factor until no non-trivial group action appears any more.
It should be clear that a lot of different choices can be made to follow
the general rule of first simplifying by homomorphisms and then using orderly
generation in the irreducible cases. Our implementation allows us to experiment
at certain stages to find a good strategy. In the most successful combination
strategies, we obtain by the implicit handling of isomorphic cases, run
times of up to ![]() graphs per second on a PC (see the small table below). We remark that we
used a labelled branching datastructure and a base change algorithm based
on [BFP] to deal with the various automorphism groups occuring during the generation
process.
graphs per second on a PC (see the small table below). We remark that we
used a labelled branching datastructure and a base change algorithm based
on [BFP] to deal with the various automorphism groups occuring during the generation
process.
Isomorphism types determined in 10 seconds
| Vertices | Degree Partition | Number of Graphs |
| 20 | (0,1,8,7,1,1,0,1,0,0,1) | 175729 |
| 30 | (0,0,4,2,4,0,2,0,10,0,6,0,2) | 2900585207520000000 |
| 50 | (0,2,10,8,11,5,8,1,2,1,0,1,1) | 192382967718269922890569744384 |
As in 3.1, the degree partitions give the numbers of vertices of degrees
0, 1, ![]() 12. Each computation was interrupted after 10.15 seconds and is therefore
incomplete. All computations were done on a PC 486DX2 with 8MB of memory.
12. Each computation was interrupted after 10.15 seconds and is therefore
incomplete. All computations were done on a PC 486DX2 with 8MB of memory.
Compared to generators using only orderly generation or only few reductions by homomorphisms, as in the present MOLGEN system, the new approach needs much more time for small cases(up to 20 - 30 vertices). This is due to the overhead caused by determining the different decompositions of the given degree partition. So the methods will have to be chosen depending on the problem size. Some optimization is still needed to make the new generator useful. The most important point seems to be that we need powerful constraints and ways to exploit them as early as possible to reduce the solution space. According to the recursion steps, this means transforming selection criteria for the resulting graphs to criteria applicable to the subgraphs which have to be combined in the recursion step. So, in this approach, one will have to study which properties are hereditary to the regular subgraphs which are the primitives.
The authors thank the referees for their comments which helped to clarify the exposition and T. Welsh for a careful reading. In addition to this paper the reader may wish to consult our WWW-pages which give information on the current MOLGEN version and, soon, the new graph generator: http://btm2xd.mat.uni-bayreuth.de
![]()
![]()
![]()
Next: References Up: Algorithms for Group Actions Previous: Basic Principles