Basic Principles

We start with some basic principles and then show how they are used in generating graphs up to isomorphism. Generally the problem of generating objects up to isomorphism can be interpreted as the problem of finding orbit representatives for a group action. Since algorithms usually also need the stabilizers of the chosen representatives, we understand by a solution of the orbit representative problem, a determination of a set of representatives together with their stabilizers.

Our approach allows us to give a solution to the generating problem that differs from that of the conventional approaches. Mathematically, one can determine the number of orbits by some variant of the Cauchy-Frobenius Lemma,see [K], which is non-constructive. This is an elegant way to get the size of the solution set. Already this method has been criticized because of its exponentional complexity. We point out however, that, as early as 1982, H. S. Wilf [Wi] gave a discussion of that problem that apparently was not recognized by complexity theory. Wilf considers the quotient of the time complexity of counting, by the time complexity of listing representatives. A counting formula is effective if this quotient tends to 0 with increasing size of the counted structures. If one is only interested in the number of orbits, his analysis shows that the Cauchy-Frobenius Lemma gives an effective solution. Since practical applications really need the solutions themselves and not just the number of solutions, there has been much effort to list orbit representatives completely. Of course, such an approach cannot lead very far when there is an exponential growth of the number of orbits. This is a motivation to generate representatives from the orbits uniformly at random.

In mathematics one can find other solutions to problems of this kind. For example, the Hauptsatz for finite abelian groups describes all finite abelian groups up to isomorphism without giving their number or listing them. Instead, there is an implicit description by lists of invariants. Though it seems intractable to find such a Hauptsatz for our problem, we make a step in that direction. So instead of listing representatives in any case, we mix listing with an implicit handling of large sections of orbits. If there is no non-trivial group action, all the objects belong to different orbits. Thus, knowing an algorithm which computes the size of the set of objects and which allows the construction of each object on demand will suffice. We say that a set O of orbits is determined if we have a rank function at hand, ranking the set O, and allowing the computation of a representative for the i-th orbit for any given rank number i. In terms of [SW] we thus require an unrank function.

To avoid a misunderstanding, we point out that we do not demand the corresponding rank function, which, given any element from any orbit, would give the rank of the orbit. Such a function would solve the general isomorphism problem for graphs, whereas finding an unrank function would be an easier problem.

We represent simple graphs as subsets of the set of all 2-element subsets of a vertex set V. Two such simple graphs are isomorphic iff they lie in the same orbit of Thus, we have to consider induced group actions. In such situations, there is often enough structure to apply algebraic decomposition techniques. The basis of this approach is to make algorithmic use of homomorphisms.

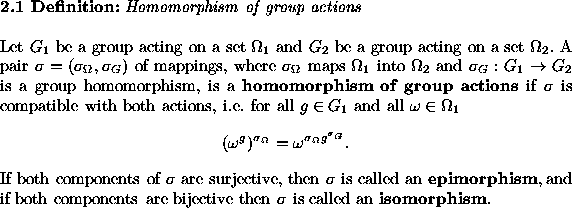
If two group actions are isomorphic with an isomorphism then carries orbit representatives and their stabilizers onto corresponding representatives and stabilizers. Thus, if isomorphisms of group actions can be found, whole sets of solutions of the orbit problem can be used many times. This allows the description of large sets of solutions implicitly in our generator, as described above.

We fix some notation we use which is partially standard. We extend the group theory notions of a normalizer and a centralizer, to the case of actions on sets of more general objects. Thus, if is a group action and then for each let and

the normalizer of in G. Similarly,

is the centralizer of in G. By abuse of notation, for a single point we denote by the stabilizer of

Suppose an epimorphism is given. Then we may use in two ways. Firstly, if a solution of the orbit problem is known in then we only have to look at the preimage sets for representatives and let the full preimage groups act on these sets respectively. We call this usage of a split.

Secondly, if a solution of the orbit problem is known in then we may use the homomorphic images of the representatives and their stabilizers to find a solution in the image domain. There is some complication, since different orbits in the preimage set may be mapped onto the same orbit. So if the image of one representative is used, one has to avoid the other image representatives for the elements of It should be noted that those points in that are mapped onto by some correspond bijectively to the cosets of in the full preimage group of The elements are just a set of coset representatives. Thus, one can also obtain the stabilizer of in this way. We call this usage of a fusion.

To point out the importance of these two interpretations, we briefly mention a typical application in construction problems. Suppose a set of representatives for the isomorphism types of a certain class of graphs is given. Then an extension step adds new subgraphs into each of these graphs. This step can be broken into two parts by the homomorphism principle. In the first part the new subgraph is added as a colored object in all possible ways up to equivalence under the automorphism group of the old graph. This is the split part of the extension. It is related to the simplification which forgets the new added subgraph. In the next half of the extension step we forget the special coloring of the subgraph. This is a simplification where we use fusion.

For another simple example using some aspects of homomorphisms, consider the generation of multigraphs. A multigraph may be obtained by gradually increasing the highest edge multiplicity by 1. In each step only the automorphism group of the chosen representative needs to be considered with its action on the set of mappings from the set of all edges of maximal degree m to the set This is of course a first application of a split. The percentage of simple graphs with non-trivial automorphism group tends to 0 with increasing number of vertices, [O]. Thus, in most cases we don't have any group action at all in these steps ( a recent implementation [Bg] demonstrates that already for a small number of vertices the automorphism groups of the multigraphs tend to become trivial very soon). This observation is trivial, but it is practically important, since in all these cases we can switch over to implicit handling instead of listing. Moreover, when graphs with trivial automorphism group combine to a bigger graph, these implicit listings may be combined yielding an implicit handling for a combinatorially exploding problem.

Nevertheless, the cases with non-trivial group action have to be considered. We demonstrate the use of homomorphism here with a simple example. Suppose a multigraph G has k edges of highest multiplicity m forming the edge set Then Aut G acts on the set of mappings from to The orbits correspond to the multigraphs with highest multiplicity m + 1 which can be deduced from G. To solve this orbit problem we may map onto , onto and Aut G onto some corresponding subgroup U of This is an isomorphism of group actions which maps onto an orbit problem which is independent of k. If we solve these orbit problems as in the case of simple graphs once and for all, we only have to note the isomorphism instead of all solutions. In particular, after a finite number of steps, no new orbit problems have to be solved for an unbounded edge multiplicity.

One can break up this orbit problem even further by reducing the action of U from to where B is an orbit of U on This may be repeated until the stabilizer of a representative mapping is trivial or the mappings are fully determined.

As usual in algebra, simplifications by homomorphisms stop at some stage when no more non-trivial homomorphisms exist. These situations are called irreducible cases. For such cases we need another tool, i.e. orderly generation[R],[F]. We now suppose that a group G acts on a finite set X. We impose on X an ordering < such that also the set of all subsets of X is lexicographically ordered. This ordering will not be compatible with the action of G, in general. It is therefore quite astonishing that such an ordering can be used to solve orbit problems. Each orbit for some contains a lexicographically minimal element which we denote as the canonical representative with respect to <. In short we say iff Then we have the following fundamental lemma[HKLMW].

Thus, we only have to enlarge representatives T of smaller cardinality by elements x which are larger than each element in T, to obtain candidates for representatives of greater cardinality. This approach can be refined noting elements y larger than each element in T which cannot enlarge T.

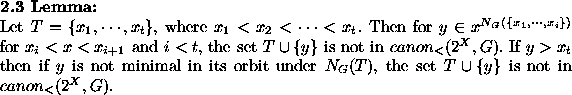
The candidates obtained after removing the cases of the preceding lemma are often called semicanonical in the special case of graph generation [KP], [Gd], [Mo].

A test for minimality for each remaining candidate S, now has to decide whether there exists some such that The obvious strategy is to run through all until either or all elements of G have been tested. Of course, there must be chosen some ordering in which the elements of G have to be considered. We take a Sims chain, also called a strong generating set, with respect to the set X ordered ascendingly, as a base This chain consists of transversals of the left cosets of in for We order these representatives r by Then we can run through all cosets under this order of r's and, for fixed r, in ascending order through for There is a case where some elements of G need not be considered in this procedure [Gd].

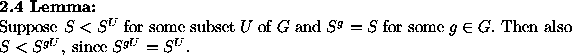
Thus, for a subgroup U which has already been tested, the whole left coset gU can be omitted if is detected. Sometimes the elements of X play a different role in a bigger context. Then one has the additional condition that each has to belong to a certain class of elements of X, tending to further restrictions for the choice of group elements. This is used in the graph generation algorithms of [McKb] and [Go], where only additions of vertices of maximal degree are considered.

Often the required solutions have to fulfill some constraints such as forbidding certain substructures. Then a check whether these constraints are fulfilled is usually much faster than a canonicity check and should be done first. It even pays to neglect the canonicity test in several consecutive extension steps, and to only check the constraints there. Then a canonicity check may reveal at a later point, that a candidate S is not minimal in its orbit, In the light of lemma 2.4 above, it is useful in such a case to determine the first extension step where this non-canonicity could have been detected. Then all further extensions of this earlier candidate must also be rejected. Depending on the selectivity of the additional constraints. a delicate balance between steps with constraint checking only, and steps with canonicity check combined with tracing back to the earliest detection point, is needed for the fastest strategy. This has been followed by MOLGEN [GKLM].

Several different strategies for solving the isomer generation problem had been pursued in different stages of the MOLGEN project. The first versions followed the DENDRAL strategy [LBFL]. There, in a finite number of steps, the isomers are constructed out of cyclic graphs. The present version uses orderly generation in filling classes of rows of the adjacency matrix [Gd] which are known to be invariant with respect to isomorphisms. For a future version we have implemented a proposal from [GKL] as a preliminary step. This generator is presently only available for simple graphs[Gr]. The generation strategy of this version makes sophisticated use of homomorphisms, and combines them with the orderly generation approach as discussed above in the irreducible cases. This new strategy is explained in the next section.