| The symmetry group of the fullerene C60 |
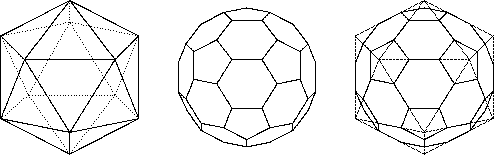
From the way of constructing the truncated icosahedron from the icosahedron (see see figure) it is clear that they both have the same symmetry group S which is isomorphic to A5´S2. The rotational symmetries form a subgroup R of S of index 2 which is isomorphic to A5. The point group symbols for S and R are Ih and I. The elements of R can be described in the following way: The 12 pentagonal faces of the fullerene C60 form 6 pairs of opposite faces. A rotation axis through the centres of two such faces is an axis of a 5-fold rotation. The 20 hexagonal faces of the fullerene C60 form 10 pairs of opposite faces through the centres of which we each have an axis of a 3-fold rotation. Finally the set of edges can be partitioned into 60 pentagonal edges surrounding the pentagonal faces and 30 hexagonal edges lying between two hexagons. The hexagonal edges form 15 pairs of opposite edges the centres of which each determine an axis of a 2-fold rotation. The full symmetry group of the fullerene C60 is computed by combining these rotations with one reflection of the fullerene.
In the present paper the symmetries of a fullerene are described as permutations of its set of vertices. This permutation representation induces a group action on the sets of all edges or faces by identifying an edge or a face with the vertices incident to it. The generators of R will be indicated by p1 and p2, whereas s stands for a reflection.
| The symmetry group of the fullerene C60 |