| The Lehmer code and reduced decompositions |
L( p):= bar (l1( p) ...ln( p)), where li( p) := | {i<j | pi> pj } | .For example
L([54132])= bar (43010).If it is clear which n is meant, then we may replace L( p) by the shorter sequence
L( p)+arising from L( p) by canceling the zeros at the end of L( p), for example
L([54132])+= bar (4301).It is not difficult to see how p can be reconstructed from L( p). Clearly p1 is the (l1 ( p)+1)-th element of n, with respect to the natural order of n. Correspondingly, p2 is the (l2( p)+1)-th element of n\{ p1 }, and so on. For example
L( p):= bar (23100) yields p=[35214].Furthermore, each L( p), pÎSn , is <= bar (n-1,n-2, ..., 1,0), i.e.
" i În: li( p) £n-i.Since there are n! such sequences in N n, we have obtained:
Corollary: The Lehmer code establishes a bijection between Sn and the set of sequences bar (l1( p) ...ln( p)) in N n, li( p) £n-i, for each i.
This shows that in fact the Lehmer code is a code for permutations.
But there is much more to say about Lehmer codes. Applying the equivalences
li( p) <= li+1( p) Û pi< p(i+1), li( p)>li+1( p) Û pi> p(i+1),we can easily derive (exercise) that right multiplication of p by the elementary transposition si=(i,i+1) has the following effect on L( p):
Lemma: For each pÎSn and each si ÎS n we haveL( psi)= bar (l1( p), ...,li-1( p),li+1( p), li( p)-1,li+2( p), ...),if li( p)>li+1( p), whileL( psi)= bar (l1( p), ...,li-1( p),li+1( p)+1,li( p),li+2( p), ...),li( p) <= li+1( p).
The main point is that the shift from p to psi amounts (cf. the Lemma above) to an increase or a decrease in
l( p):= åili( p)by 1. Hence the following holds:
Corollary: The sum l( p) of the entries of the Lehmer code L( p) of pÎSn is equal to the minimal number of elementary transpositions si which are needed in order to express p as a product of elementary transpositions. Moreover, this yields a canonic way of expressing p as a product of l( p) elementary transpositions by decreasing the rightmost nonzero entry of the Lehmer code by 1 and iterating this process until each entry is equal to zero.
We therefore call l( p) the
reduced length
of p and we call such an expression of p as a product of
l( p) elementary transpositions, which is of minimal length, a
reduced decomposition.
A reduced decomposition of [54132], for example, is obtained from the following sequence of manipulations
of Lehmer codes, according to the
corollary:
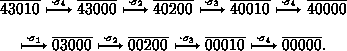
This shows that
[54132]= s4 s3 s2 s1 s4 s3 s2 s4is a reduced decomposition. Try to compute the reduced composition of some permutations.
The lemma also shows how we can obtain all the reduced decompositions of a given permutation:
Corollary: The complete set of reduced decompositions of p is obtained by carrying out all the successive multiplications that reduce the Lehmer sequence by 1, according to the Lemma.
| The Lehmer code and reduced decompositions |