| Rothe diagram and inversions |
p=[ p1, ..., pn], or p=[ p1 ...pn], if possible.In order to visualize permutations we can use a board consisting of boxes in the second quadrant, where we put a black button · into the box with the pair of coordinates (i,k) if and only k= pi, obtaining the Rothe diagram R( p) of p. This diagram was introduced by H. A. Rothe already in 1800. For example R([54132]) is equal to
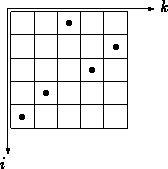
The list notation gives rise to the Lehmer code which we are going to describe next. In order to do this we consider the set I( p) of inversions of p:
I( p):= {(i,j) În2 | i<j, pi> pj }.An easy check (exercise) shows that the following holds:
Lemma: If we represent the inversion (i,j) of p by a white button o at ( pj,i), then we fill exactly the boxes of the Rothe diagram of p where the black button of the row is in a column to the right and where the black button of the column is lower down.
The resulting diagram L( p) is called the Lehmer diagram
of p. For example, the superposition of the Rothe diagram and the Lehmer
diagram of p:=[54132] is
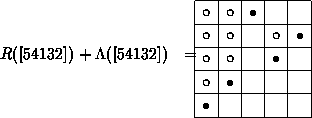
There is a program, which calculates the number of inversions of a given permutation.
| Rothe diagram and inversions |