Counting by stabilizer class

Counting by stabilizer class

The preceding chapter was devoted to the enumeration of orbits by weight, a problem that can be solved by an easy refinement of the Cauchy-Frobenius Lemma. In the present chapter we shall introduce another variation of this lemma in order to count orbits by stabilizer class. Recall that the elements of an orbit have as their stabilizers a conjugacy class [~U] of subgroups of G. We say that [~U] is the type 

of this orbit. The set of orbits of type [~U] , for a given subgroup U of G, is called the [~U] -stratum and indicated by

[~U] \\\X.

First we consider the lattice L(G) of subgroups of G. The group G is supposed to be finite and hence L(G) is a locally finite poset with respect to the inclusion order <= and we shall be able to apply in particular the Moebius Inversion. We assume that the subgroups Uⁱ of G are numbered in such a way that

  Uⁱ <= U^k Þ i <= k.

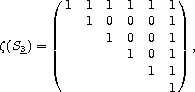
In this case the zeta-matrix as well as the Moebius-matrix of G, defined by

z(G):=(z(Uⁱ,U^k)), and m(G):=(m(Uⁱ, U^k))=z(G)^-1,

are upper triangular. Let us consider an easy example: G:=S₃. This group has the lattice of subgroups shown in figure,

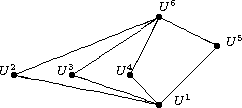
where U¹=á1ñ, U²=á(12)ñ, U³=á(13)ñ, U⁴=á(23)ñ, U⁵=á(123)ñ, and U⁶= S₃. Thus and so

m(S₃)=(

1	-1	-1	-1	-1	3
	1	0	0	0	-1
		1	0	0	-1
			1	0	-1
				1	-1
					1

).

In order to calculate | [~U] \\\X | , we consider, for the finite action _GX and U <= G, the sets

X_U:={x | " gÎU: gx=x}.

Burnside called the order | X_U | of this set the mark of U on X. We express it in terms of lengths of strata:

| X_U | =å_{x:U <= Gx}1=å_{V:U <= V <= G}å_x:V=Gx1=å_{V:U <= V <= G}(1)/( | [~V] | )å_x:GxÎ[~V] 1

=å_{V:U <= V <= G}( | G/V | )/( | [~V] | )å_{tÎT:GtÎ[~V]} 1 =å_{V:U <= V <= G} ( | G/V | )/( | [~V] | ) | [~V] \\\X | ,

=å_Vz(U,V) ( | G/V | )/( | [~V] | ) | [~V] \\\X | ,

where T denotes a transversal of the orbits of G on X. By Moebius Inversion this equation is equivalent to:

| [~U] \\\X | =( | [~U] | )/( | G/U | ) å_Vm(U,V) | X_V | .

In order to simplify this expression we consider the set [~L] (G) consisting of the conjugacy classes of subgroups of G:

[~L] (G):={[~U] ₁,...,[~U] _d}, with representatives U_iÎ[~U] _i.

(Uⁱ should not be mixed up with U_i!) Putting

  b_ik:=( | [~U] _i | )/( | G/U_i | )å_{VÎ[~U] k}m(U_i,V), and B(G):=(b_ik),

we can now reformulate the equation above in terms of this matrix B(G), which I call the Burnside matrix of G (in fact Burnside considered the inverse of B(G) and called it the table of marks; we shall return to this matrix later). It is in fact the following lemma (and not the lemma of Cauchy-Frobenius that is quite often named after Burnside, see the remarks on history in the chapter containing the comments and references) which is

  Burnside's Lemma If _GX is a finite action, then the vector of the lengths | [~U] _i\\\X | of the strata of G on X satisfies the equation

We can apply this now in order to enumerate the G-classes on Y^X by type. Since fÎY^X is fixed under each gÎU_i if and only if f is constant on each orbit of U_i on X, we obtain:

Corollary: The number of symmetry classes of G on Y^X of type [~U] _i is the i-th entry of the one column matrix

Thus, for example, the number of k-graphs on v vertices which are of type [~U] _j, U_j a subgroup of S_v, is the element in the j-th row of the matrix 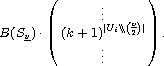For v:=4, an application of the Burnside matrix shown in the appendix yields the following table.

type\k	0	1	2	3	4
[~U] _1	0	0	11	100	465
[~U] _2	0	2	21	84	230
[~U] _3	0	1	9	36	100
[~U] _4	0	0	0	0	0
[~U] _5	0	2	9	24	50
[~U] _6	0	0	0	0	0
[~U] _7	0	0	1	4	10
[~U] _8	0	2	6	12	20
[~U] _9	0	2	6	12	20
[~U] _10	0	0	0	0	0
[~U] _11	1	2	3	4	5
å	1	11	66	276	900

The last column of this table shows among other things that there exist altogether 900 4-graphs on 4 vertices, and that exactly 465 of them are of type [~U] ₁. Furthermore we note that the fourth, the sixth and the tenth row of this table consist of zeros only, which stimulates the question whether this also holds for bigger k. These rows belong to U₄ simeq A₃, U₆ simeq C₄ and U₁₀ simeq A₄. A shorter formulation of this question reads as follows: Do A₃, C₄ or A₄ occur as automorphism groups of multigraphs? More generally: Which subgroups of G occur as stabilizers of mappings fÎY^X? In order to answer this question we recall * which says that the stabilizer of f in the symmetric group S_X is the subgroup

(S_X)_f=Å_yÎYS_Xy.

This implies

Corollary: The stabilizers of the fÎY^X are the subgroups U <= G, the corresponding permutation group bar (U) of which satisfies

bar (U)=S_a Ç bar (G),

where bar (G) corresponds to G, and S_a is the direct sum of the symmetric groups on the orbits of U:

S_a:=Å_wÎU\\XS_w.

We can now answer one of the questions posed above concerning automorphism groups of graphs.

Corollary: The alternating group A_v does not occur as an automorphism group of a multigraph on v vertices, if v >= 3.

Proof: The assumption bar (A)_v = S_aÇbar (S)_v yields, as A_v acts transitively on [v choose 2], that S_a is the full symmetric group on [v choose 2], and hence bar (A)_v = bar (S)_v, which is a contradiction if v>2.

A similar result holds for the cyclic group C_v (see exercise *) and the alternating subgroup A_v-1 (exercise *). Another immediate consequence of * is an expression for the number of orbits of prescribed length. Using the abbreviation, for U,V <= G:

  m(U,[~V] ):=å_WÎ[~V] m(U,W),

we derive from *

Corollary: If _GX is a finite action, then the number of orbits of length k of G on X is equal to

(1)/(k)å_{i: | G/Ui | =k} | [~U] _i | å_j m(U_i,[~U] _j) | X_Uj | ,

and in particular the number of primitive orbits , i.e. of orbits of the (maximal) length | G | , is equal to

(1)/( | G | )å_jm(1,[~U] _j) | X_Uj | .

We consider a well known example from Galois theory.

Examples: Consider the finite field GF(q),q:=p^m,p a prime number, and its extension field GF(qⁿ) of degree n. By Galois theory its Galois group G is generated by the Frobenius isomorphism 

s:GF(qⁿ) -> GF(qⁿ):x -> x^q,

which is of order n:

G=ásñ={1,s,...,s^n-1} simeq C_n.

Moreover GF(qⁿ) possesses a normal basis, which means that there exist xÎ GF(qⁿ) such that {x,sx,..., s^n-1x} is a GF(q)-basis of GF(qⁿ). Expressing the elements of GF(qⁿ) in terms of this basis as GF(q)-linear combinations

å_i=1ⁿf(i)sⁱx, f(i)ÎGF(q),

we can identify them with vectors f=(f(1),...,f(n))Îqⁿ on which the Galois group generator s acts as a cyclic shift. Hence the existence of a normal basis shows that the action of the Galois group G on GF(qⁿ) is isomorphic to the canonical action of the cyclic group C_n on qⁿ. Denoting by G\\ _{| G |} X the set of orbits of (maximal) length | G | , we now evaluate the number

| G\\ _{| G |} GF(qⁿ) | = | C_n \\_n qⁿ |

of orbits of maximal length n of the Galois group. As the cyclic group C_n has a subgroup lattice isomorphic to the lattice of divisors d of n, the Moebius function m of L(C_n ) is the number theoretic Moebius function. Moreover the unique subgroup of order d, where d is a divisor of n, in the cyclic group C_n is generated by the power (1...n)^n/d of the full cycle and, by *, this power consists of n/d disjoint cycles, each of which has the length d. Furthermore fÎqⁿ is fixed under this subgroup á(1...n)^n/dñ if and only if f is constant on the disjoint cyclic factors of (1...n)^n/d. Hence, by *, we obtain

  | G\\ _{| G |} GF(qⁿ) | = | C_n \\_n qⁿ | = (1)/(n)å_{d | n}m(d)q^n/d,

where m denotes the number theoretic Moebius function. Note that this number of primitive orbits is also equal to the number of irreducible monic polynomials with zeros in GF(qⁿ) and coefficients in GF(q), since by Galois theory a root of a polynomial is mapped onto a root by each element of the Galois group. More generally, we can consider the orbits of maximal length of C_n on mⁿ. The numbers

l_mn:= | C_n \\_n mⁿ | =(1)/(n)å_{d | n}m(d) m^n/d

are called Dedekind numbers. Some of the smaller ones are shown in the following table:

m\n	1	2	3	4	5
1	1	0	0	0	0
2	2	1	2	3	6
3	3	3	8	18	48
4	4	6	20	60	204
5	5	10	40	150	624

.

The fÎmⁿ can be considered as words 

f=f(1)...f(n)

of length  n over the alphabet  m. The lexicographically smallest elements in the orbits (for short: f£C_n (f)) of length n of C_n on mⁿ form the canonic transversal

L_n(m):={fÎmⁿ | | C_n (f) | =n,f£C_n (f)};

its elements are called the Lyndon words of length n over the alphabet m. The union of all these sets

L(m):=È_nL_n(m)

is called the Lyndon set over the alphabet m. Now we consider an arbitrary word fÎmⁿ. As each letter iÎm forms a Lyndon word of length 1, there exists a uniquely determined longest left factor l₁(f)=f(1)... of f which is a Lyndon word. The same holds for the remaining part w of f=l₁(f)w, and hence there is a unique decomposition

  f=l₁(f)l₂(f)...l_l(f)(f)

of f into Lyndon words such that in the right part l_i(f)...l_l(f)(f) the Lyndon word l_i(f) is the maximal left Lyndon factor. This decomposition is called the Lyndon decomposition of f, and the number l(f) of factors is called the Lyndon length of f. Even more, the Lyndon decomposition can also be described as follows (exercise *)

 Lyndon's Theorem The factors l_i(f) of the decomposition * defined above are lexicographically nonincreasing:

l₁(f)³l₂(f)³...³l_l(f)(f).

Conversely, each decomposition into nonincreasing Lyndon words is the decomposition * introduced above.

Using the Lyndon length we can define the following generating function:

l_n(x,m):=å_fÎmⁿx^l(f),

which generates the numbers of words of length n over m with prescribed Lyndon length. V. Strehl has recently noticed and proved the remarkable fact that this function is symmetric in x and m. For example

l₃(x,m)=(1)/(3!)(x³m³ +3(x³m²+x²m³-x²m²)+2(x³m+m³x)-2xm).

In order to prove this it is enough to show that, for all k,m,n in N^*, the identity l_n(k,m)=l_n(m,k) is true. We consider a second alphabet k, say, and the corresponding set k^* of all the words over k. Let F(m,k) denote the set of all the mappings f:L(m) -> k^* such that all but a finite number of values f(f) are equal to the empty word epsÎk^*. We map f onto [^f] :L(k) -> m^*, defined as follows: Let [^f] ÎL(k) occur in the Lyndon decompositions of f(f_i), say with the multiplicity m(f(f_i),[^f] ). We can assume without restriction that f_i³f_i+1, for each i. Then put

[^f] ([^f] ):=f₁·...·f_i·...·f_{im(f(fi),[^f] )}·...·f_n.

Let us consider an example. Assume that f:L(3) -> 2^* has the following nonempty images (we separate Lyndon factors by dots):

f(12)=2·12, f(113)=12·1·1, f(2)=2·12·1,

then [^f] has just the following nonempty images:

[^f] (1)=2·113·113, [^f] (12)=2·12·113, [^f] (2) =2·12.

It is clear that f can be reconstructed from [^f] , and Lyndon's Theorem assures that this is true also in general. Hence f -> [^f] is a bijection between F(m,k) and F(k,m). Now we introduce a norm by putting

| | f | | :=å_fÎL(m) | f | | f(f) | ,

where | w | denotes the length (number of letters) of the word w. An important property of the norm is the identity

| | f | | =å_fÎL(m) | f | å_{[^f] ÎL(k)} | [^f] | ·m(f(f),[^f] )= | | [^f] | | ,

where the last equation holds since m(f(f),[^f] )=m([^f] ([^f] ),f), by construction of [^f] .

Lemma:  (Strehl) For all k,m,nÎN^* we have the identity

l_n(k,m)=l_n(m,k).

Proof: Consider fÎmⁿ and the corresponding subset L_fÍF(m,k), consisting of the following f: f(f')=eps if and only if the Lyndon word f' is not a factor of f, while otherwise f(f')Îk^m(f,f'). Easy checks show that | L_f | =k^l(f) and

fÎÈ_fÎmⁿL_f iff | | f | | =n,

which allows to complete the proof:

l_n(k,m)=å_fÎmⁿk^l(f)= | {fÎF(m,k) | | | f | | =n } |

= | {[^f] ÎF(k,m) | | | [^f] | | =n} | = å_{[^f] Îkⁿ}m^{l([^f] )}=l_n(m,k).

Now we use a further indeterminate z in order to define the formal power series

L(x,m):=å_nl_n(x,m)zⁿ.

Lyndon's Theorem shows that the following is true:

L(x,m)=Õ_n((1)/(1-k·zⁿ))^l_mn,

so that we obtain the following surprising result:

Õ_n((1)/(1-k·zⁿ))^l_mn=Õ_n((1)/(1-m·zⁿ))^l_kn,

which implies in particular (put k:=1 and note that l_1n=1 if n=1, and l_1n=0, otherwise):

The cyclotomic identity For all k,m,nÎN^* and the Dedekind numbers l_mn=(1)/(n)å_{d | n}m(d) m^n/d we have the identity

Õ_n((1)/(1-zⁿ))^l_mn =(1)/(1-m·z).

E: Prove the following identity for the elements of the Burnside matrix:

b_ik=m([~U] _i,U_k)( | [~U] _k | )/( | G/U_i | ), where m([~U] _i,U_k):= å_{VÎ[~U] i}m(V,U_k).

E: Prove that the cyclic group C_v does not occur as an automorphism group of a multigraph on v vertices, if v³2.

E: Prove that the subgroup A_v-1 of A_v does not occur as an automorphism group of a multigraph on v vertices, if v³3.

E:   Prove *.

Counting by stabilizer class