Sums of cycle indicators, recursive methods

Sums of cycle indicators, recursive methods

If A_X denotes the alternating group on the finite set X then, by Pólya's Theorem, the coefficient of the monomial P_y y^c(f,y) in C(A_X,X | åy) is equal to the number of A_X-classes of mappings with the same content as f. If we exclude the trivial case | X | =1, then the A_X-class of f differs from its S_X-class if and only if its stabilizers (S_X)_f and (A_X)_f are equal, and if these classes differ, then the S_X-class of f consists of two A_X-classes.

The stabilizer of fÎY^X in S_X is the following direct sum of the symmetric groups on the inverse images of the yÎY:

  (S_X)_f=Å_y S_Xy, where X_y:=f^-1[{y}].

The stabilizer of f in A_X is the intersection of (S_X)_f with A_X. As each noninjective f is left fixed by a transposition while each injective f has the identity subgroup as its stabilizer, we obtain

Corollary: The stabilizers of fÎY^X in S_X and in A_X are the same, or, equivalently, they both are equal to the identity subgroup, if and only if f is injective.

Thus the difference of cycle indicators of alternating and symmetric groups has the following useful interpretation (recall figure):

Corollary: For | X | >1 the polynomial

C(A_X,X | åy)-C(S_X,X | åy)

is the generating function for the enumeration of the injective S_X-classes on Y^X by weight.

Corresponding results hold for cyclic and dihedral groups. Also these arguments can be considered as a certain kind of involution principle. In fact we obtain in the same way the following generalization of the corollary above (recall the corollary on chiral actions):

Corollary: If _GX denotes a chiral action, then

C(G⁺,X | åy)-C(G,X | åy)

is the generating function for the enumeration by weight of the G-classes on Y^X which split over G⁺.

Besides these differences of cycle indicator polynomials we can form sums of cycle indicator polynomials of series of groups, e.g. we obtain (by simply comparing coefficients) the equation

  å_n=0^¥ C(S_n ,n)=expå_k=1^¥[z_k choose k]ÎQ[[z₁,z₂,...]],

if C(S₀,0 | p(u)):=1 and where Q[[z₁,z₂,...]] denotes the ring of formal power series over Q in the indeterminates z₁,z₂,.... An immediate consequence is

  å_n=0^¥ C(S_n,n | p(u))=exp å_k=1^¥ [1 choose k]p(u^k) Î Q[[u]],

This sum is of great interest since it can be used for a recursion method which we are going to describe next.

Example: A graph is called a tree if and only if it is connected and does not contain any cycle. A tree with a single distinguished vertex is called a rooted tree. Figure shows the smallest rooted trees. The root is distinguished by indicating it as a circle while the other vertices are indicated by a bullet.

The smallest rooted trees

  If r(x) denotes the generating function for the enumeration of rooted trees by their number of vertices, then figure shows that

r(x)=x+x²+2x³+4x⁴+....

We claim that this formal power series satisfies a recursion formula in terms of cycle indicator polynomials of symmetric groups.

Lemma:   r(x)=xå_n=0^¥ C(S_n ,n | r(x)).

Proof: It is clear that the generating function for the enumeration of rooted trees is equal to the sum over all nÎN of the generating functions of rooted trees with root degree n, i.e. where the root is incident with exactly n edges. It therefore remains to evaluate the generating function for the enumeration of trees with root degree n. Denote by R the set of all the rooted trees. A rooted tree with root degree n can be considered as an orbit of S_n on the set R ⁿ. If we now give an element of R the weight x^v, where v denotes the number of vertices of the rooted tree in question, then we obtain the power series xC(S_n ,n | r(x)) which therefore is the desired generating function for the enumeration of rooted trees with root degree n by their number of vertices. This completes the proof. An application of the above exponential expressions and for the sum of the cycle indicator polynomials of finite symmetric groups as an exponential formal power series allows to rewrite the recursion formula for the generating function of the rooted trees in the following way:

Corollary: The formal power series r(x) which generates the numbers of rooted trees by number of vertices satisfies the recursion formula

r(x)=x·expå₁^¥ [r(x^k) choose k].

This recursion together with a suitable program system, like MAPLE or MACSYMA, allows to evaluate the smallest numbers of rooted trees, some of which are shown in the following table:

n	b_n	n	b_n
1	1	11	1842
2	1	12	4766
3	2	13	12486
4	4	14	32973
5	9	15	87811
6	20	16	235381
7	48	17	634847
8	115	18	1721159
9	286	19	4688676
10	719	20	12826228

Similar arguments apply in each case when the structure in question consists of a certain and well defined number of structures of the same kind. Lower down we shall see how a systematic theory can be developed which covers this and many other cases (there are various approaches, the books are full of them, for example the book of Goulden/Jackson gives an approach that covers very many cases in a different and more elementary way compared to the theory of species which is briefly indicated down below).

Example: Each graph is a disjoint union of connected graphs (a graph is called connected if and only if from each of its vertices we can reach any other vertex by walking along suitably chosen edges). These connected subgraphs are well defined, and they are called the connected components. Thus the generating function g(x)=å_vg_vx^v of the graphs and the generating function c(x)=å_v c_vx^v for the connected graphs are related as follows:

  g(x)=å_n=0^¥ C(S_n ,n | c(x))=expå_k=1^¥ [c(x^k) choose k].

As we already know that

g_v=[1 choose v!]å_pÎSv2^{c(bar (p))},

we can use above exponential formula in order to evaluate the entries of the following table:

v	g_v	c_v
1	1	1
2	2	1
3	4	2
4	11	6
5	34	21
6	156	112
7	1044	853
8	12346	11117
9	274668	261080
10	12005168	11716571

Further examples show up in the sciences. It was already briefly mentioned that the origins of this theory of enumeration lie in chemistry and the problem of isomerism. A few remarks concerning the history are therefore in order. It was already in the 18th century when Alexander von Humboldt conjectured that there might be chemical substances which are composed by the same set of atoms but have differend properties. In his book with the title ''Versuche über die gereizte Muskel- und Nervenfaser, nebst Vermutungen über den chemischen Prozeß in der Tier- und Pflanzenwelt``, published in 1797, he writes (on page 128 of volume I):

But it needed a quarter of a century to develop the anaytical methods that allowed to find out what the atomic constituents of a chemical molecule are. These methods were developed in particular by J. L. Gay-Lussac and J. von Liebig, who were the first to prove von Humboldt's conjecture to be true. Here is a sentence taken from a paper of Gay-Lussac that describes their discovery:

It needed some time to realize that a new phenomenon was discovered, J. J. Berzelius gave it the name isomerism. Chemists tried to find out what the reason is by sketching molecules. Here are three of these attempts to draw the molecule of C₂H₅OH: The first attempt is due to Couper:

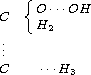
The next one is the way how Loschmidt drew this molecule:

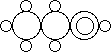
The breakthrough towards a solution of this problem is due to Alexander Crum Brown, who used a variation of Loschmidt's method by putting the circles of atoms that are assumed to be connected somehow apart but joining them by edges in order to emphasize the connection. Here are his drawings for the alcohol C₃H₇OH:

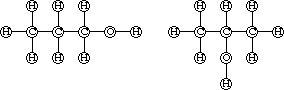
This introduction of molecular graphs solved the problem of isomerism by showing that there may exist different graphs that correspond to a given chemical formula (which prescribes in fact the degree sequence, which is the sequence of valencies of the atoms in the given formula). Moreover it gave rise to the development of graph theory (there are of course also other birthdays of graph theory known, for example Euler's solution of the Königsberg bridge problem, and Kirchhoff's invention of electric circuits as well as Hamiltons game called ''trip around the world``), and it stimulated the combinatorial theory of enumeration since the question of chemical isomerism is at first glance equivalent to the problem of constructing all the graphs which are connected and which have a given edge degree sequence. Let us consider, for example, the chemical formula C₃H₇OH again, or, more generally the formula C_nH_2n+1OH. The problem is to construct all the graphs which correspond to each of these formulae, i.e. all the graphs that consist of n vertices of degree 4 (the carbon atoms are of that valency) together with 2n+2 vertices of degree 1 (the hydrogen) and one of degree 2 (the oxygen) which must have a neighbour of degree 1 (so that a hydroxyl group -OH occurs). This problem amounts to the construction of rooted trees, as, by a well-known result of graph theory, such degree sequences can be satisfied by trees only (the cyclomatic number is zero in this case). The root represents the substructure ºC-O-H, so that the root degree is <= 3. Consider the two examples shown above which correspond to the formula C₃H₇OH. As the carbon atoms are of valency 4, we can make life easier by neglecting the hydrogen atoms, so that the skeletons remain, which correspond to the rooted trees with 3 vertices. From each one of these structures we can reconstruct the original molecular graph and hence the desired generating function a(x) for the numbers of alcohols satisfies the recursion

  a(x)=xå_n=0³C(S_n ,n | a(x)).

Sums of cycle indicators, recursive methods