Conjugation

Conjugation

Having described the elements of S_n , we show which of them are in the same conjugacy class, i.e. in the same orbit of the group S_n on the set S_n under the conjugation action. In order to do this, we first note how rpr^-1 is obtained from the permutation p: 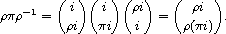Thus, in terms of cyclic factors of p, rpr^-1 arises from

p = ( ...i pi ...) ...

by simply applying r to the points in the cycles of p:

  rpr^-1= ...( ...ri r( pi) ...) ... .

(For any mapping j:S -> T we mean by j(s)=t that s has to be replaced by t and not that t is replaced by s, as it is sometimes understood!) This equation shows that the lengths of the cyclic factors of p are the same as those of rpr^-1. It is easy to see that, conversely, for any two elements p, sÎS_n with the same lengths l _n of cyclic factors there exists a rÎS_n such that rpr^-1= s. Hence the lengths of the cyclic factors of p characterize its conjugacy class. To make this more explicit, we introduce the notion of (proper) partition of n Î N, by which we mean any sequence a= ( a₁, a₂, ...) of natural numbers a_i which satisfy

" i : a_i >= a_i+1, and å_i a_i=n.

The a_i are called the parts of a. The fact that a is a partition of n is abbreviated by

a|¾n.

If a|¾n then there exists an h such that a_i=0 for all i>h. We may therefore write

a=( a₁, ..., a_h),

for any such h. The minimal h with this property will be denoted by l( a) and called the length of a. The following abbreviation is useful in the case when several nonzero parts of a are equal, say a_i parts are equal to i,i În:

a= (n^a_n,(n-1)^a_n-1, ...,1^a₁).

If a_i=0, then i^a_i is usually omitted, e.g. (3,1²)=(3,1,1,0, ...). For pÎS_n the ordered lengths a_i( p),i Î c( p), of the cyclic factors of p in cycle notation form a uniquely determined proper partition

a( p)=( a₁( p), a₂( p), ..., a_{c( p)} ( p)) |¾n,

which we call the cycle partition of p. The corresponding n-tuple

a( p):=(a₁( p), ...,a_n( p))

consisting of the multiplicities a_i( p) of the parts of length i in a( p) is called the cycle type of p. Correspondingly we call an n-tuple a:=(a₁, ...,a_n) a cycle type of n if and only if each a_i Î N, and åi ·a_i =n. This will be abbreviated by

a |¾| n.

Conjugation