Cycle decomposition

Cycle decomposition

The points which form the first row need not be written in their natural order, e.g. 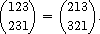Keeping this in mind, we call a permutation pÎS_n a cyclic permutation or a cycle if and only if it can be written in the form 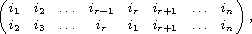where r ³1. In order to emphasize r we also call it an r-cycle . We note that in this case the orbits of the subgroup generated by this permutation are the following subsets of n: {i₁, ...,i_r }, {i_r+1 }, ..., {i_n }. We therefore abbreviate this cycle by (i₁, ...,i_r)(i_r+1) ...(i_n), where the points which are cyclically permuted are put together in round brackets. 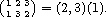For example Commas which seperate the points may be omitted if no confusion can arise (e.g if n £10), and 1-cycles can be left out if it is clear which n is meant. Hence we can write p=(i₁ ...i_r) for the r-cycle introduced above. This cycle p can also be expressed in terms of i₁ alone: p=(i₁ pi₁ ...p^r-1i₁). Using all these abbreviations and denoting by 1:=(1) ...(n) the identity element, we obtain for example

S ₃= {1,(12),(13),(23),(123),(132) }.

There are the elements of the symmetric group S_n in cycle notation. The notation for a cyclic permutation is not uniquely determined, since

  (i₁ ...i_r)=(i₂ ...i_r i₁)= ...=(i_r i₁ ...i_r-1).

2-cycles are called transpositions . The order of a cycle (i₁ ...i_r), i.e. the order of the cyclic group á(i₁ ...i_r) ñ generated by this cycle, is equal to its length :

  | á(i₁ ...i_r) ñ | =r.

Two cycles p and r are called disjoint , if the two sets of points which are not fixed by p and r are disjoint sets. Notice that, for example, 1=(1)(2)(3) and (123) are disjoint cycles. Disjoint cycles p and r commute, i.e. pr= rp. (We read compositions of mappings from right to left, so that ( pr)x= p( rx).) Each permutation of a finite set can be written as a product of pairwise different disjoint cycles, e.g. 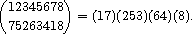There are some more examples for the cycle decomposition of a permutation.

The disjoint cyclic factors not =1 of pÎS_n are uniquely determined by p and therefore we call these factors together with the fixed point cycles of p the cyclic factors of p. Let c( p) denote the number of these cyclic factors of p (including 1-cycles), let l _n be their lengths, nÎ c( p) (recall that c( p)= {1, ...,c( p) }), choose, for each n an element j _n of the n-th cyclic factor. Then

  p= Õ _{nÎ c( p)} (j _n pj _n ...p^{l _n-1}j _n).

This notation becomes uniquely determined if we choose the j _n so that

  " m Î N : j _n £p^mj _n, and " n<c( p) : j _n<j _n+1.

If this holds, then the notation as was given above is called the (standard) cycle notation for p. We note in passing that the sets {j _n, pj _n, ..., p^{l _n-1}j _n } of points which are cyclically permuted by p are just the orbits of the cyclic group ápñ generated by p.

Cycle decomposition