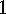Sylows Theorem




Next: Products of Actions
Up: Actions
Previous: Action on k-subsets
The following is a very important application of actions on 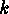 -subsets:
The regular representation of
-subsets:
The regular representation of  yields, in accordance with
yields, in accordance with  , the
, the  -sets
-sets 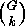 ,
for
,
for 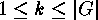 . If
. If  is finite and
is finite and  a prime
dividing
a prime
dividing 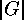 , say
, say 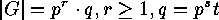 , where
, where  does not divide
does not divide 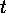 , then we can put
, then we can put 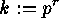 and
consider the particular
and
consider the particular  -set
-set 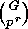 ,
as H. Wielandt did in his famous
proof of Sylow's Theorem
in order to show that
,
as H. Wielandt did in his famous
proof of Sylow's Theorem
in order to show that  possesses
subgroups of order
possesses
subgroups of order 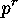 . His argument runs as follows:
. His argument runs as follows:
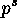 is the exact power of
is the exact power of  dividing the order of
dividing the order of
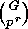 . This is
clear from
. This is
clear from
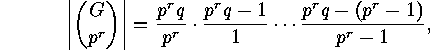
as each power of  contained in the denominator cancels.
Thus
contained in the denominator cancels.
Thus 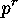 -subsets
-subsets 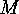 exist, the orbit length
of which is not divisible by
exist, the orbit length
of which is not divisible by 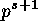 .
We consider such an
.
We consider such an 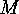 and show that its stabilizer
and show that its stabilizer 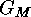 is of
order
is of
order 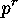 by proving that
by proving that 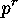 is both an upper and lower bound:
For each
is both an upper and lower bound:
For each 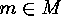 and
and 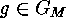 we have that
we have that 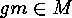 , hence
, hence

On the other hand, the fact that 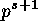 does not divide the orbit length
does not divide the orbit length
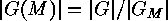 yields
yields

This proves the first item of
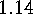 .
. Sylow's Theorem
Assume
Sylow's Theorem
Assume  to be a finite group
and
to be a finite group
and  to be a prime divisor of its order. Then
to be a prime divisor of its order. Then
-
 contains
subgroups of order
contains
subgroups of order 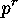 , for each power
, for each power 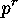 dividing its
order
dividing its
order 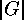 .
.
The subgroups 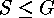 of the maximal
of the maximal  -power order are called
the Sylow
-power order are called
the Sylow  -subgroups
of
-subgroups
of 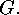 They have the following properties:
They have the following properties:
- Each
 -subgroup
-subgroup 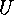 of
of  is contained
in a suitable Sylow
is contained
in a suitable Sylow  -subgroup
-subgroup 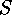 .
.
- Any two Sylow
 -subgroups of
-subgroups of  are conjugate subgroups.
are conjugate subgroups.
The proof of the second and third item follows from a consideration of double
cosets. Assume a  -subgroup
-subgroup 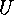 of
of  and a Sylow
and a Sylow  -subgroup
-subgroup 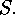 Then
we derive from
Then
we derive from  that
that
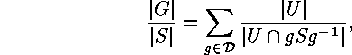
where 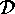 denotes a transversal of
denotes a transversal of 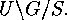 If all the intersections in the denominator on the right hand side were proper subgroups
of
If all the intersections in the denominator on the right hand side were proper subgroups
of 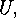 then the right hand side were divisible by
then the right hand side were divisible by 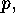 which contradicts the left hand
side. Hence there must exist a
which contradicts the left hand
side. Hence there must exist a 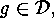 such that
such that 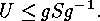 Since
Since
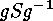 is a Sylow
is a Sylow  -subgroup, too,
-subgroup, too, 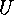 is contained in a Sylow subgroup, which
proves the second item.
is contained in a Sylow subgroup, which
proves the second item.
The third item follows by taking for 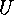 a Sylow
a Sylow  -subgroup
-subgroup 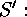
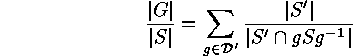
shows that 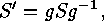 for a suitable
for a suitable 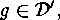 where
where 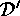 denotes a transversal of
denotes a transversal of 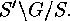

This example shows clearly that the consideration of suitable group
actions can be very helpful, at least in group theory. Applications
to other fields of mathematics will follow soon.
Exercises
E 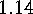 .
. Prove that the number of Sylow
Prove that the number of Sylow  -subgroups divides the order of
-subgroups divides the order of  and is congruent 1 modulo
and is congruent 1 modulo 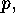 for each prime divisor of the order of
for each prime divisor of the order of 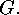




Next: Products of Actions
Up: Actions
Previous: Action on k-subsets
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
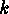 -subsets:
The regular representation of
-subsets:
The regular representation of  yields, in accordance with
yields, in accordance with  -sets
-sets 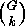 ,
for
,
for 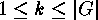 . If
. If  is finite and
is finite and  a prime
dividing
a prime
dividing 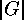 , say
, say 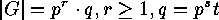 , where
, where  does not divide
does not divide 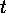 , then we can put
, then we can put 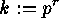 and
consider the particular
and
consider the particular  -set
-set 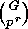 ,
as H. Wielandt did in his famous
proof of Sylow's Theorem
in order to show that
,
as H. Wielandt did in his famous
proof of Sylow's Theorem
in order to show that  possesses
subgroups of order
possesses
subgroups of order 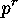 . His argument runs as follows:
. His argument runs as follows:
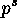 is the exact power of
is the exact power of  dividing the order of
dividing the order of
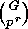 . This is
clear from
. This is
clear from
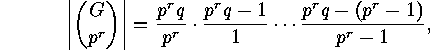
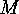 exist, the orbit length
of which is not divisible by
exist, the orbit length
of which is not divisible by 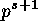 .
We consider such an
.
We consider such an 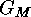 is of
order
is of
order 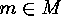 and
and 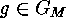 we have that
we have that 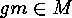 , hence
, hence

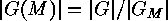 yields
yields

 .
.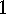 Sylow's Theorem
Sylow's Theorem 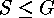 of the maximal
of the maximal 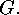 They have the following properties:
They have the following properties:
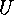 of
of 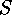 .
.
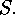 Then
we derive from
Then
we derive from 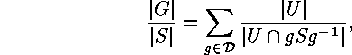
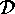 denotes a transversal of
denotes a transversal of 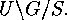 If all the intersections in the denominator on the right hand side were proper subgroups
of
If all the intersections in the denominator on the right hand side were proper subgroups
of 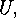 then the right hand side were divisible by
then the right hand side were divisible by 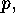 which contradicts the left hand
side. Hence there must exist a
which contradicts the left hand
side. Hence there must exist a 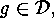 such that
such that 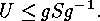 Since
Since
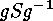 is a Sylow
is a Sylow 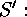
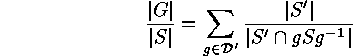
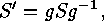 for a suitable
for a suitable 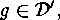 where
where 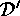 denotes a transversal of
denotes a transversal of 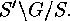

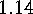 .
.