blatt 2

Prof. Dr. R. Laue                                                                            WS0304                                 Informatik I
                                Übungsblatt 2
                                Abgabe: 13.11. vor der Vorlesung

URL: /axel/informatik1_ws0304_blatt2.html
Dieses Übungsblatt ist in Zweiergruppen zu bearbeiten. Auf dem Blatt bitte Übungsgruppentag angeben. Um den Übungsschein zu erhalten, muß man 50% der Punkte erreichen und aktiv am Übungsbetrieb teilnehmen. D.h Vorrechnen, Bearbeitung von mindestens 80% der Übungsblätter.

Jede Aufgabe auf einem eigenen Blatt (mit Namen und Gruppe und Matrikelnummern).

Aufgabe 4 - Schubfachprinzip - (4 Punkte)- eigenes Blatt

Zeigen Sie, daß es keinen endlichen Automaten mit dem Eingabealphabet 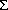= {0,1} gibt, der die Sprache

L = { 0ⁿ  1ⁿ | n>0 }

akzeptiert. Hinweis: Wenden Sie das Schubfachprinzip auf die Menge der Zustände an.
Schubfachprinzip: Hat man m>n Dinge in n Schubfächern, so gibt es ein Schubfach mit mindestens 2 Dingen.

Aufgabe 5 - Beispielrechner - (2+3+1+2 Punkte)- eigenes Blatt

Schreiben Sie ein Programm für den Beispielrechner aus der Vorlesung (ohne Adressberechnung) der die Aufgabe 4 löst. Das Programm liest eine Folge von 0'en, dann eine Folge von 1'en. Die Folge der 1'en wird durch eine neue 0-Folge beendet. Dass Programm soll eine 1 ausgeben, wenn es gleichviel 0'en und 1'en waren, ansonsten ist die Ausgabe eine 0. Das Programm endet danach.

Beispiel: Die Eingabefolge 000011110 hat die Ausgabe 1, die Eingabefolge 10 hat die Ausgabe 0. Bei der Eingabefolge 011111111.... terminiert das Programm nicht.

Erstellen Sie ein Nassi Shneiderman Diagramm zu Ihrem Programm. (2 Punkte)
Schreiben Sie das Programm für den Beispielrechner und kommentieren Sie es zeilenweise. (3 Punkte, ohne Kommentar 0 Punkte)
Bestimmen Sie die Anzahl der ausgeführten Befehle im Fall der Eingabe 000011110. (1 Punkt)
Bestimmen Sie die Anzahl der ausgeführten Befehle im Fall der Eingabe 0ⁿ1ⁿ0 als Funktion von n. (2 Punkte)

Aufgabe 6 - Jahreszahlerkenner- (4+3 Punkte)- eigenes Blatt

Geben Sie den Übergangsgraphen zu einem endlichen Automaten, der gültige Jahreszahlen erkennen soll an. D.h. das Eingabealphabet besteht aus den Ziffern 0,1,2,..,9 und dem Sonderzeichen #, welches ein beliebiges anderes Zeichen kodiert. Eine Ziffernfolge zwischen dem Sonderzeichen # wird als Jahreszahl interpretiert. Liegt diese Zahl zwischen 1 und 2003 soll der Automat in einem Zustand aus der Endzustandsmenge wechseln und im weiteren in diesem verbleiben. Beispiel: #345# ist o.k. 123 ist ok 123454# ist nicht o.k. ###11# ist ok #001# ist ok #0000#2222# ist nicht o.k. #3333#2002# ist o.k.

Schreiben Sie das zugehörige 5 Tupel auf. (1 Extrapunkt falls weniger als 11 Zustände)