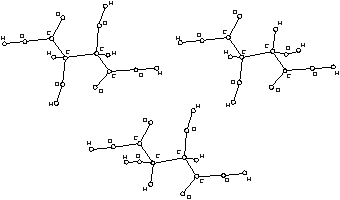
Figure 2. Configurational isomers of tartaric acid.
Department of Mathematics, University of Bayreuth, D-95440 Bayreuth, Germany
E-mail: wieland@btm2d1.mat.uni-bayreuth.de
In the automatization of molecular structure elucidation, generators for constitutional and configurational isomers are indispensable tools. Sophisticated computer programs of this kind are based on a mathematical theory of the construction of discrete structures. First, we will describe the basic principles for the generation of constitutional isomers, starting with the notions of group actions and ending up with recent improvements with respect to hybridization constraints. The second part is devoted to the generation of all configurational isomers to a given structural isomer. The underlying mathematical concepts as well as the techniques for computing spatial realizations are discussed. The outlined theory is implemented in the program system MOLGEN, which provides a fast and efficient tool for structure elucidation, running under DOS, MS-Windows, OS/2 and SUN-Solaris.
1
INTRODUCTION
In the past two decades, molecular structure elucidation was propeled by the
development of computer programs for the automatic construction of isomers.
Three types of approach can be distinguished (for details see a review [1,2]): The first, in essence, seeks to assemble
structures from standard fragments [3-5]. The
next utilizes a precise mathematical representation to reduce the problem to a
(possibly rather large) catalog of substructures and computes all irredundant
combinations [6-10].
The last Ansatz does not rely on any catalog, but calculates the
compounds as connectivity matrices by orderly generation
[11-13].
A common maxim of all approaches is that to be useful in everyday's work in a laboratory, a structure generator must fulfil at least two requirements: a) It must be exhaustive, i.e. it must generate all isomers corresponding to the given data. b) It must be irredundant, i.e. no isomers should occur twice. In order to meet these requirements, sophisticated algorithms based on mathematical theory must be applied. The efficiency of the programs depends on how the problem of redundancy is treated; algorithms using algebraic techniques generally excel over pure combinatorial methods.
For the algorithmic treatment, chemical compounds must be modeled on a certain level of abstraction. The following levels are commonly used:
Figure 2. Configurational isomers of tartaric acid.

2
GROUP ACTIONS
Graphs and multigraphs must be labeled to be stored in a computer's memory. But
the labeling, i.e. the numbering of the vertices, is not relevant for
molecules. So methods for classifying all representations of graphs must be
applied. Hence a key notion for structure generation is that of group action.
Let G denote a finite group and X a finite set. An action of G on X is described by a mapping
The action defines substructures on G and X:
A labeled m-graph with p vertices is an element f from X to {0,1,...,m} with X:=p^[2]:= {{i,k}| 1 lower or equal i<k lower or equal p}, where f({i,k})=j means that the pair {i,k} of vertices connected by an edge of degree j; if j=0, the vertices are not connected. To derive all (unlabeled) multigraphs we have to compute the orbits of the action of the symmetric group Sp on X to {0,1,...,m}. Early algorithms tried to determine the orbits by comparing each potential representative to all previously found. The expenditure on such computations, however, is enormous. A better way is to calculate canonical representatives only, e.g. representatives that are maximal within their orbits.
By writing f in X to {0,1,...,m} as a vector
f=/f(x1),f(x2),.../ we can formulate the
basic algorithm as follows:
Using this algorithm, certain problems have to be overcome:
The data contains two elements:
This approach bears several advantages:
| Restriction | Number of isomers |
|---|---|
| - | 2,558,517 |
| max. double bonds | 2,434,123 |
| no O-O | 360,594 |
|
H-distribution (2,1,1,0,0,0,1,1,1,1,0,0) |
35,058 |
|
Multiplicities (Csp3,Csp3,Csp3,Csp2,Csp2,Csp2, Osp3,Osp3,Osp3,Osp3,Osp3,Osp2) |
990 |
(The current version of the user interface in MOLGEN (vide infra) does not allow the input of hydridizations. This is to be incorporated together with further developments of the generator [23].)
With this algorithm the total variety of structures corresponding to the given data can be computed - regardless as to whether they can be synthesized or even exist in reality. As opinions of what is stable and what is not are subject to changes over the years, the check on plausibility is left to the user. We include, however, a list of rather unlikely substructures (like a 4-ring with an sp-hybridized carbon or a 3-ring with three sp2-hybridized carbons) to cull isomers thought to be unrealistic. Since this list is composed from data files, it can freely be altered according to the individual needs.
If we take dioxin C12O2H4Cl4, for example, with the skeleton
A number of approaches [25-28] have been reported, which are all more or less effective. What we want to discuss here, are the mathematical foundations.
The generation of configurational isomers after the algorithm by Nourse et al. [25] is performed in three steps:

The automorphism group is constructed in our algorithm in two steps: First the vertices of the graph are partitioned such that there cannot be automorphisms that map vertices from different partitions onto one another. Next all possible permutations within the partitions are checked as to whether they are also automorphisms of the graph. The result is stored as a SIMS chain [29].
To be able to write the ligands of a center as (ordered) tuples, the
environment of the center is considered as locally placed in space. Although
this is easily incorporated in the algorithm via the initial numbering of the
vertices, it is a useful method for interpreting changes of the order of the
ligands as changes of the configuration (depending on the sign).
As an example we consider the following structure:

Table 2. The CSG of the structure III, where e:=(0)(1) and i:=(01).
| (e,e,e,e,e,e,e,e); | 1 |
| (e,e,i,e,e,i,e,e); | 1 |
| (e,i,e,e,e,e,e,i); | 1 |
| (e,i,i,e,e,i,e,i); | 1 |
| (i,e,e,i,e,e,e,e); | (12)(57) |
| (i,i,e,i,e,e,e,i); | (12)(57) |
| (i,e,i,i,e,i,e,e); | (12)(57) |
| (i,i,i,i,e,i,e,i); | (12)(57) |
| (e,i,i,e,e,e,e,e); | (03)(46) |
| (e,i,e,e,e,i,e,e); | (03)(46) |
| (e,e,i,e,e,e,e,i); | (03)(46) |
| (e,e,e,e,e,i,e,i); | (03)(46) |
| (i,i,i,i,e,e,e,e); | (03)(12)(46)(57) |
| (i,e,i,i,e,e,e,i); | (03)(12)(46)(57) |
| (i,i,e,i,e,i,e,e); | (03)(12)(46)(57) |
| (i,e,e,i,e,i,e,i); | (03)(12)(46)(57) |
So the permutations of the automorphism group must be extended by mappings which represent the ability of a ligand permutation to change the configuration of the center. These mappings will be called inversions. (In Nourse's notation [30] these are called superscripts.) They are determined as follows:
| (0, 0, 0, 0, 0, 0, 0, 0) | (0, 1, 0, 0, 0, 0, 0, 1) | |
| (0, 0, 0, 0, 0, 0, 0, 1) | (0, 1, 0, 0, 0, 0, 1, 0) | |
| (0, 0, 0, 1, 0, 0, 0, 0) | (0, 1, 0, 1, 0, 0, 0, 0) | |
| (0, 0, 0, 1, 0, 0, 0, 1) | (0, 1, 0, 1, 0, 0, 0, 1) | |
| (0, 0, 0, 1, 0, 0, 1, 0) | (0, 1, 0, 1, 0, 0, 1, 0) | |
| (0, 0, 0, 1, 0, 0, 1, 1) | (0, 1, 0, 1, 0, 0, 1, 1) | |
| (0, 0, 1, 1, 0, 0, 0, 0) | (0, 1, 1, 1, 0, 0, 0, 0) | |
| (0, 0, 1, 1, 0, 0, 0, 1) | (0, 1, 1, 1, 0, 0, 0, 1) | |
| (0, 1, 0, 0, 0, 0, 0, 0) | (0, 1, 1, 1, 0, 0, 1, 0) |
So we can define the configuration symmetry group (CSG) as C(g,b) := { (E;f) | f in A(g,b)}, and it proves [28] to be a subgroup of the wreath product [14,15] of the S2 over {1,...,s} with A(g,b), if there are s stereocenters in the molecule.
The CSG of the cyclobutan-derivative III is listed in table 2. The stereocenters are numbered.
After the construction of C(g,b), we are able to verify the potential stereocenters by the following rule: if there is a permutation in the automorphism group whose restriction to the ligands of a potential stereocenter is odd, this atom is a real stereocenter only if the non-fixed ligands themselves contain at least one stereocenter. The direction of the search should be from the outer to the inner regions of the molecule in order to reduce the expenditure and to avoid overlooking a center.
For the actual generation of the stereoisomers, we remark that with s stereocenters we get all essentially different configurational isomers by computing a transversal of C(,)\\{1,...,s} to {0,1}. This transversal can be computed with (an enhanced version of) the basic algorithm from section 2.
A list with the stereoisomers of III as (0,1)-sequences is shown in table 3. As any structural isomer has one or more configurational isomers, the numbers of possible stereoisomers of a set of constitutional isomers can be computed, as shown in table 4.
It is also interesting to compare the sizes of both sets of isomers with each other. In fig. 3 the ratios of stereoisomers per structural isomer are printed. While the numbers of constitutional isomers of CnHm have peaks at 4 to 8 hydrogens, the ratio decreases monotonously as the number of hydrogens increases.
As discussed above, this algorithm also generates all isomers without regard to their realizability. The evaluation of the results is left to the user.
The generation algorithm in the form discussed above can only handle stereocenters of valence 3 or 4. It is, however, possible to extend it to higher valences [31].
| CiHj | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 |
|
|
|
|
- | - | - | - | - | - | - | ||||||||||||||||||||||
| 4 |
|
|
|
|
|
- | - | - | - | - | - | ||||||||||||||||||||||
| 5 |
|
|
|
|
|
|
- | - | - | - | - | ||||||||||||||||||||||
| 6 |
|
|
|
|
|
|
|
- | - | - | - | ||||||||||||||||||||||
| 7 |
|
|
|
|
|
|
|
|
- | - | - | ||||||||||||||||||||||
| 8 |
|
|
|
|
|
|
|
|
|
- | - | ||||||||||||||||||||||
| 9 |
|
|
|
|
|
|
|
|
|
|
- | ||||||||||||||||||||||
| 10 |
|
|
|
|
|
|
|
|
|
|
|
Figure 3. Ratios of stereoisomers per structural isomer
This can be done by automatic model builders [32-34] or by geometric construction starting from reference coordinates, e.g. obtained by a molecular mechanics calculation [35]. We followed the second way, basing our method on earlier approaches [27, 36].
The first step is to identify the configuration in the reference placement. This is performed by geometric analysis: Let a stereocenter (position X) have its neighbours in the positions X1, X2, X3 and X4. Calculate n := X1X2 x X1X3. If n.(X1-X) <0, return 1; else return 0. The double bonds are examined analogously.
Next the ligands at the centers are reflected. In the recursive procedure four cases are considered:
IV
Its four stereoisomers are shown in fig. 4. Another example, now for case 3, is provided by the spiro-compound V. There are 8 configurational isomers of this molecule; two of them are drawn in fig. 5
V
Figure 4. Stereoisomers of structure IV
Figure 5. Configurations (0,0,0,0) and (0,1,0,1) of the eight stereoisomers of structure V
As the users of such software differ considerably, MOLGEN is available [37] for DOS, Microsoft Windows, IBM OS/2 and Sun SOLARIS/Motif in different versions. Demos are accessible from the WorldWide Web document http://btm2xd.mat.uni-bayreuth.de/molgen.
A prominent application of structure generating programs are automated structure elucidation systems. At present MOLGEN is incorporated in SpecInfo [38]. There a given spectrum is interpreted via a large spectra database, yielding a set of substructures. MOLGEN generates candidates based thereon, which can afterwards be verified.
But a structure generator can also be useful in chemical education [19,20], e.g. to visualize the variety of isomerism, in pharmacology [39], and various other fields.
We are grateful to the German Federal Ministry of Education, Science, Research and Technology (BMBF) for financial support.