Canonical Representatives for Nested Structures
A chemical molecule has several properties which can be used to represent the molecule as a nested structure.
The attributes may be atom names, atom numberings, valences, bond angles, dihedral angles, distances, electric charges, etc.
Correspondingly, there are the obvious domains: Integers, real numbers, strings, etc.
A structural formula describing a molecule is then built from a set of vertices by adding atom names, forming edges connecting two
vertices, adding multiplicities and bond lengths, forming triples assigned with bond angles and quadruples assigned with dihedral
angles, etc., and finally calling the result the nested structure molecule.
Definition
Let 
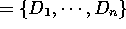 be a set of domains
and let
be a set of domains
and let 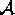
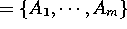 be a set of attributes
where to each attribute
be a set of attributes
where to each attribute 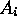 some domain
some domain 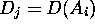 is assigned.
An atomic structure is a tuple
is assigned.
An atomic structure is a tuple 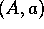 where
where 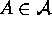 and
and 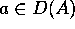 . An atomic structure has nesting level 0.
For l > 0 a structure S of nesting level l consists of a set
or a sequence
of structures of levels strictly smaller than l,
called the components of S,
where at least one of them has level l-1.
. An atomic structure has nesting level 0.
For l > 0 a structure S of nesting level l consists of a set
or a sequence
of structures of levels strictly smaller than l,
called the components of S,
where at least one of them has level l-1.
Isomorphism of Nested Structures
The reason for detailing the definition in so many tiny steps is that we need each such step for a fast identification of the
objects. We want to take into account all properties of the structure as soon as possible. So, two such nested structures will be
considered to be equivalent or, technically speaking, isomorphic, if one differs from the other only by replacing atomic values by
other atomic values according to some given classification.
Thus, all numbers of vertices may be permuted giving different but, of course, equivalent representation of the same molecule. But we will
not allow to replace atom names, say Cl by Na.
Since there are n! permutations of n equivalent atomic values there are also as many different ways to replace a
structure by an equivalent one. The recognition problem is solved if we can compute a unique representation out of these.
For that purpose we impose orderings on the domains and on 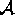 . Then, sets of atomic values
can be represented by sequences, formed by the elements in ascending order. The sequences are ordered lexicographically. For
sequences of values from different attributes also the ordering of the attributes has to be used. Thus, nested structures can be
compared according to the lexicographical ordering of the induced orderings of the components.
. Then, sets of atomic values
can be represented by sequences, formed by the elements in ascending order. The sequences are ordered lexicographically. For
sequences of values from different attributes also the ordering of the attributes has to be used. Thus, nested structures can be
compared according to the lexicographical ordering of the induced orderings of the components.
An obvious solution of the recognition problem would be to declare the smallest representation of an object by a nested structure
of a fixed type as its canonical representation. But this idea does not take the special properties of the current object into
account. Therefore the CAS numbering uses some variant of the Morgan numbering procedure using some rules to restrict the number
of different possibilities that have to be considered.
This approach still has some deficiencies, since it is intimately tied to that special structure and the computational effort is
still high. Also, integrating informations on some 3D-properties or electronic charge is not obvious. We therefore describe a
refinement which can be applied to all nested structures of the same type. The approach at the same time generalizes an approach
from computational graph theory [3] to these nested structures, bounding backtrack branches by rules which use
the ordering.
Iterated Classification
As in any conventional approach we build classes of elements which cannot be distinguished by properties of the actual structured
object. Of course, then only elements of the same class may be permuted among each other. This classification starts with the
given classification on the atom set and from that it steps up the different levels, classifying also the higher level components.
Since the entries of higher components are already classified, we can use the class numbers of these entries in order to
classifiy the components themselves. From classes of higher components we then can again classify the entries. As the development
of the Morgan algorithm showed we must respect a possibly existing classification in each level of components to avoid circles.
Thus, we always only refine classes obtained so far.
The algorithm realizing this idea is called iterated classification, since in an iterative process a given
classification is refined using only the current information on the object encoded by the nested structure.
If all classes consist of a single element after the iterated classification then we have no further choice for different
numbering and we have found a canonical representation.
Though in many cases already one call of the iterated classification with the obvious start classification
suffices, some cases, as for example structures with symmetries, need a more sophisticated approach.
Backtracking
Suppose that after the iterated classification stopped there remain different classes of length greater than 1.
Then for a class of length t one has to try t elements as being the first element of its class. We cannot avoid
these choices but we can first choose the smallest possible t
This is the strategy proposed by [1] after an analysis of the complexity of backtracking by
[2].
Now trying all further possibilities of arranging the remaining t-1 elements of that class would afford t! choices.
But we are in a better position. We have already distinguished one element of the class as being the first. So we may use this
as a new refinement of this class and start iterated classification again [3]. This usually results in a
drastical refinement of the previous classes. So, on iterating this strategy we will soon end up
with distinct classes. Remembering that these classifications depended on arbitrary selections of elements from classes, one has
to compare the results lexicographically and choose the canonical representative from these results. As usual in backtracking, one
can keep the best solution known so far and after each iterated classification step compare the incomplete result to that. If any
result obtainable on the actual track cannot beat the current champion, the whole track can be avoided.
So, combining the ideas presented above we get an algorithm which produces a canonical representative defined by the algorithm.
The representative will not be the overall minimal representative. But this algorithmic representative results from an analysis
of the difficulty to recognize the structure, done by the algorithm.
There is one further important point to make. Suppose we compare two entries for equivalence during the classification.
Then the values may be known only up to a certain error. So, depending on the structure, different conclusions can be drawn
from a slight difference. An angle, or a distance, within a rigid ring part of a molecule will require a much better agreement
of the values than at the place where a ligand is bound to a skeleton. So, the decision to represent a molecule by local
properties results in a more flexible similarity concept than comparing coordinate vectors in a 3D-space.
1: C. W. H. Lam, G. Butler: "A general backtrack algorithm
for the isomorphism problem of combinatorial objects", J. of Symb. Comp. 1 (1985),
363-381
2: D. E Knuth: "Estimating the efficiency of Backtrack
programs" Math. of Comput. 29 (1975), 121-136
3: B. D. McKay: "Computing automorphisms and canonical
labelings of graphs" Springer LN in Math. 686 (1977), 223-232
Previous: Abstract
Next: Adaption to 2-D Molecules
© Chr. Benecke, Oct. 1995

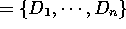 be a set of domains
and let
be a set of domains
and let 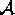
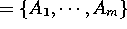 be a set of attributes
where to each attribute
be a set of attributes
where to each attribute 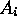 some domain
some domain 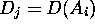 is assigned.
An atomic structure is a tuple
is assigned.
An atomic structure is a tuple 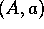 where
where 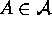 and
and 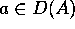 . An atomic structure has nesting level 0.
For l > 0 a structure S of nesting level l consists of a set
or a sequence
of structures of levels strictly smaller than l,
called the components of S,
where at least one of them has level l-1.
. An atomic structure has nesting level 0.
For l > 0 a structure S of nesting level l consists of a set
or a sequence
of structures of levels strictly smaller than l,
called the components of S,
where at least one of them has level l-1.
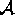 . Then, sets of atomic values
can be represented by sequences, formed by the elements in ascending order. The sequences are ordered lexicographically. For
sequences of values from different attributes also the ordering of the attributes has to be used. Thus, nested structures can be
compared according to the lexicographical ordering of the induced orderings of the components.
. Then, sets of atomic values
can be represented by sequences, formed by the elements in ascending order. The sequences are ordered lexicographically. For
sequences of values from different attributes also the ordering of the attributes has to be used. Thus, nested structures can be
compared according to the lexicographical ordering of the induced orderings of the components.