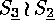 . The set of proper
partitions characterizing the conjugacy classes of
. The set of proper
partitions characterizing the conjugacy classes of 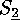 is
is
A numerical example is provided by 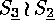 . The set of proper
partitions characterizing the conjugacy classes of
. The set of proper
partitions characterizing the conjugacy classes of 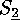 is
is
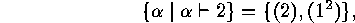
the set of corresponding cycle types is

Thus the types of  turn out to be
turn out to be
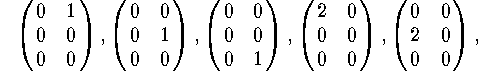
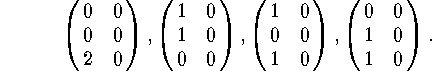
The orders of the conjugacy classes are 6,18,12,1,9,4,6,4,12.
We now describe an interesting action of 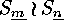 which
is in fact an action of the form
which
is in fact an action of the form 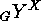 .
.
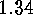 .
.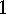 Example
The action of
Example
The action of 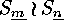 on
on 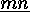 is obviously
similar to the following
action of
is obviously
similar to the following
action of
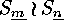 on the set
on the set 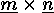 :
:
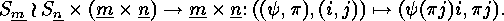
The corresponding permutation group on 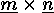 will be denoted by
will be denoted by

and called the composition
of 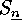 and
and  , while
, while

will be used for the permutation group on 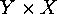 , induced by the
natural action of
, induced by the
natural action of 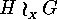 on
on 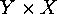 .
.
The action of the wreath product 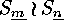 on
on 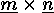 induces a natural action of
induces a natural action of 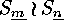 on the set
on the set
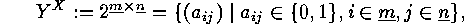
i.e. on the set of 0-1-matrices consisting of 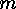 rows and
rows and 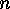 columns:
columns:
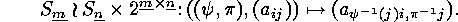
Since 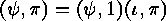 ,
we can do this in two steps:
,
we can do this in two steps:
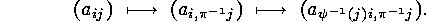
Hence we can first of all permute the columns of  in
such a way that the numbers of 1's in the columns of the resulting matrix
is nonincreasing from left to right:
in
such a way that the numbers of 1's in the columns of the resulting matrix
is nonincreasing from left to right:
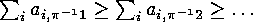 And after having carried out
this permutation with a suitable
And after having carried out
this permutation with a suitable  , we can find
a
, we can find
a 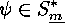 that moves the 1's of each column in flush top
position. This proves that the orbit of
that moves the 1's of each column in flush top
position. This proves that the orbit of 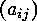 under
under 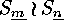 is characterized by an element of the form
is characterized by an element of the form
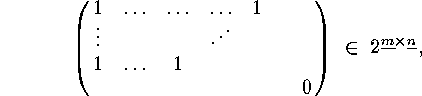
i.e. by a proper partition of 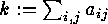 . Hence the orbits of
. Hence the orbits of
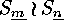 on
on 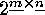 are characterized by the
proper partitions
are characterized by the
proper partitions 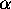 , where each part
, where each part  and where the total number of parts is
and where the total number of parts is 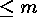 :
:
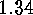 .
.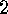 Corollary
There exists a natural bijection
Corollary
There exists a natural bijection
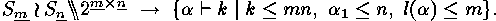
Hence an application of the Cauchy-Frobenius Lemma yields the following formula for the number of partitions of this form:
which can be made more explicit by an application of ![]() .
.
