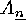 of
of
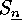 . In order to show this we introduce the sign
. In order to show this we introduce the sign
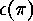 as follows:
as follows:
Another important fact exhibits a normal subgroup 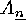 of
of
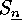 . In order to show this we introduce the sign
. In order to show this we introduce the sign
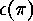 as follows:
as follows:
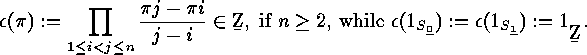
As 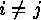 implies
implies 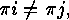 we have
we have 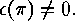 Moreover,
the following sets of pairs are equal:
Moreover,
the following sets of pairs are equal:
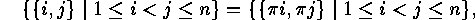
and so
we have 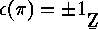 . Furthermore
. Furthermore  is a homomorphism of
is a homomorphism of 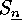 into
into
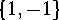 :
:
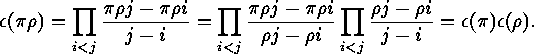
This proves
is a homomorphism which is surjective for each
is a normal subgroup of
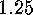 .
.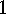 Corollary
The sign map
Corollary
The sign map
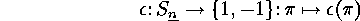
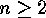 .
Hence its kernel
.
Hence its kernel
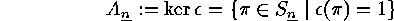
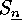 :
:
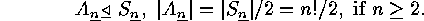
The elements of 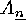 are called even
permutations, while the elements of
are called even
permutations, while the elements of 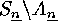 are called
odd
permutations.
Correspondingly, an
are called
odd
permutations.
Correspondingly, an  -cycle is even
if and only if
-cycle is even
if and only if  is odd.
There is a program to compute the
sign of various
permutations.
is odd.
There is a program to compute the
sign of various
permutations.