©  OLGEN |
exit | by Joachim Braun and Christoph Rücker |
| © OLGEN |
exit | by Joachim Braun and Christoph Rücker |
· TodCon
: Todeschini, R.; Consonni, V. Handbook
of Molecular Descriptors, Wiley-VCH, Weinheim and
· Trin:
Trinajstić, N. Chemical Graph Theory,
2nd edition, CRC Press, Boca Raton, FL, 1992
A, A (incl. H) and N_H are descriptors of the category 'arithmetic'.
Notation in text: 
, 
and 
is the number of atoms
excluding H atoms. is the number of atoms
including H atoms. is the number of H
atoms.
A (incl. H) see 0.
N_H see 0.
rel. N_H, rel. N_C, rel. N_O, rel. N_N, rel. N_S, rel. N_F, rel. N_Cl, rel. N_Br, rel. N_I and rel. N_P are descriptors of the category 'arithmetic'.
Notation in text: 
, 
, 
, 
, 
, 
, 
, 
, 
and 
Relative means divided by the number of atoms (inclusive H
atoms):
Correspondingly , , , , , , , , and .
N_C, N_O, N_N, N_S, N_F, N_Cl, N_Br, N_I and N_P are descriptors of the category 'arithmetic'.
Notation in text: 
, 
, 
, 
, 
, 
, 
, 
and 
is the number of C atoms
in a molecule.
Correspondingly , , , , , , and .
rel. N_C see 3.
N_O see 4.
rel. N_O see 3.
N_N see 4.
rel. N_N see 3.
N_S see 4.
rel. N_S see 3.
N_F see 4.
rel. N_F see 3.
N_Cl see 4.
rel. N_Cl see 3.
N_Br see 4.
rel. N_Br see 3.
N_I see 4.
rel. N_I see 3.
N_P see 4.
rel. N_P see 3.
B and B (incl. H) are descriptors of the category 'arithmetic'.
Notation in text: 
, 
is the number of bonds
in the H-suppressed molecule. is the number of bonds in a molecule containing H atoms.
B (incl. H) see 22.
loc. B and loc. B (incl. H) are descriptors of the category 'arithmetic'.
Notation in text: 
and 
is the number of
localized bonding electron pairs in an H-suppressed molecule. Aromatic π-electrons
are delocalized and therefore not counted here.
is analogous to but includes bonds to H
atoms.
loc. B (incl. H) see 24.
n- and n- (incl. H) are descriptors of the category 'arithmetic'.
Notation in text: 
and 
is the number of
single bonds in an H-suppressed molecule. is analogous to but includes bonds to H
atoms.
rel. n- and rel n- (incl. H) are descriptors of the category 'arithmetic'.
Notation in text: 
and 
rel. n- is relative to the number of bonds of an H-suppressed molecule:
Analogous is:
For see 26, for see 22, for see 28 and for see 23.
n- (incl. H) see 26.
rel. n- (incl. H) see 27.
n=, n# and n aromatic are descriptors of the category 'arithmetic'.
Notation in text: 
, 
and 
is the number of
double bonds, the number of triple
bonds and is the number of
aromatic bonds.
rel. n=, rel. n= (incl. H) , rel. n#, rel. n# (incl. H), rel. n aromatic and rel. n aromatic (incl. H) are descriptors of the category 'arithmetic'.
Notation in text: 
, 
, 
, 
, 
and 
is relative to the
number of bonds in an H-suppressed molecule. is relative to the
number of bonds in a molecule with H atoms.
Correspondingly , , and .
rel. n= (incl. H) see 31.
n# see 30.
rel. n# see 31.
rel. n# (incl. H) see 31.
n aromatic see 30.
rel. n aromatic see 31.
rel. n aromatic (incl. H) see 31.
C is a descriptor of the category 'arithmetic'.
Notation in text: 
For molecules (connected graphs) is defined as:
MW and MW (incl. H) are descriptors of the category 'arithmetic'.
Notation in text: 
and 
is the sum of the atomic
weights in an H-suppressed molecule. The atomic weight is that of the natural
abundance isotope mixture. 
takes account of the H
atoms.
Source:
· TodCon,
page 332
mean AW and mean AW (incl. H) are descriptors of the category 'arithmetic'.
Notation in text: 
and 
mean AW is defined as:
Analogous :
For and see 40 and 42. For and see 0 and 1.
MW (incl. H) see 40.
mean AW (incl. H)
see 41.
W is a descriptor of the category 'topological'.
Notation in text: 
W is the half-sum of the entries of the distance-matrix of the H-suppressed molecule:
where is the number of non-H
atoms and 
is the entry in the ith
row and the jth column of the distance matrix.
For see 0 and for see distance matrix.
Source:
· Wiener, H. Structural Determination of Paraffin Boiling Points. J. Am. Chem. Soc. 1947, 69, 17-20
· TodCon, page 497
M_1 is a descriptor of the category 'topological'.
Notation in text: 
is the sum over the squares
of the vertex degree of each atom in an H-suppressed molecule:
where is the number of non-H
atoms and 
is the number of
neighbours of atom i in an H-suppressed molecule.
For see 0. For see vertex degree.
Source:
· Gutman,
· TodCon, page 509
· Trin,
page 226
M_2 is a descriptor of the category 'topological'.
Notation in text: 
is the following sum
over all edges:
where is the number of
neighbours of atom i in an H-suppressed molecule.
For see vertex degree.
Source:
· Gutman,
· TodCon, page 509
· Trin,
page 226
m^M_1 and m^M_2 are descriptors of the category 'topological'.
Notation in text: 
and 
is the sum over the
squares of the reciprocal vertex degree of each atom in an H-suppressed
molecule:
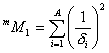
is defined as the
following sum over all edges:
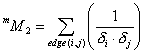
where is the number of non-H
atoms and is the number of
neighbours of atom i in an H-suppressed molecule. 
stands for modified.
For see 0. For see vertex degree.
Source:
· Nikolić,
S.; Kovačević, G.; Miličević, A.; Trinajstić, N. The
m^M_2 see 47.
0^Chi is a descriptor of the category 'topological'.
Notation in text: 
This is the zeroth descriptor in the series m^Chi with m = 1, 2, 3, …
Notation in text: 
The definition of :
where is the number of non H-atoms
and is the number of
neighbours of atom i in an H-suppressed molecule.
For see 0. For see vertex degree.
The definition of :
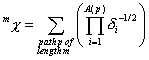
with 
. The sum runs over all paths of length (this is the number of
edges of the path). 
is the number of the
atoms in a path 
. The product runs over all atoms of path . is the vertex degree
of the ith atom in path .
For see vertex degree.
Source:
· Randić, M. On Characterization of Molecular Branching. J. Am. Chem. Soc. 1975, 97, 6609-6615
· Kier, L. B.; Murray, W. J.; Randić, M.; Hall, L. H. Molecular Connectivity V: Connectivity Series Applied to Density. J. Pharm. Sci., 1976, 65, 1226-1230
· Kier,
L. B.; Hall L. H. The Nature of Structure-Activity Relationships and their
Relation to Molecular Connectivity. Eur.
J. Med. Chem., 1977, 12, 307-312
· Kier,
L. B.; Hall L. H. Molecular Connectivity
in Structure-Activity Analysis. Research-Studies Press - Wiley,
· TodCon,
pages 84-85
· Trin,
page 226
1^Chi see 49.
2^Chi see 49.
0^Chi^s is a descriptor of the category 'topological'.
Notation in text: 
is the zeroth member in the series m^Chi^s with m = 1, 2, 3,
…
Notation in text: 
The definition of :
where is the number of non-H
atoms and is the number of
neighbours of atom i in an H-suppressed molecule. 
is the principal
quantum number of atom i (for C, N, O, F: 
=2; for Si, P, S, Cl: =3).
For see 0. For see vertex degree.
The definition of :
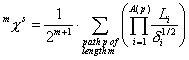
with . The sum runs over all paths of length (this is the number of
edges in the path). is the number of the
atoms in a path . The product runs over all atoms in path . is the vertex degree
of the ith atom in path . is the principal
quantum number of atom i in path .
For see vertex degree.
Source:
· Zefirov,
N. S.; Palyulin, V. A. QSAR for Boiling Points of “Small” Sulfides. Are the
“High-Quality Structure-Property-Activity Regressions” the Real High Quality
QSAR Models? J. Chem. Inf. Comput. Sci.
2001, 41, 1022-1027
· TodCon,
pages 88-89
1^Chi^s see 52.
2^Chi^s see 52.
3^Chi^s see 52.
3^Chi^s (cluster) is a descriptor of the category 'topological'.
Notation in text: 
The definition of is:
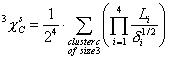
The sum runs over all clusters of size 3:
The product runs over all four atoms of cluster 
. is the vertex degree
of the ith atom in cluster . is the principal
quantum number of atom i in cluster .
For see vertex degree.
Source:
· TodCon,
pages 88-89
0^Chi^v is a descriptor of the category 'topological'.
Notation in text: 
is the zeroth member
of the series m^Chi with m = 1, 2, 3, …
Notation in text: 
The definition of :
where is the number of non-H
atoms and 
is the valence vertex
degree of atom i in an H-suppressed molecule.
For see 0. For see valence vertex degree.
The definition of :
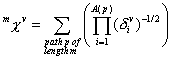
with . The sum runs over all paths of length (this is the number of
edges of the path). is the number of atoms
in a path . The product runs over all atoms of path .
For see valence vertex degree.
Source:
· Kier, L. B.; Murray, W. J.; Randić, M.; Hall, L. H. Molecular Connectivity V: Connectivity Series Applied to Density. J. Pharm. Sci., 1976, 65, 1226-1230
· Kier,
L. B.; Hall L. H. The Nature of Structure-Activity Relationships and Their
Relation to Molecular Connectivity. Eur.
J. Med. Chem. 1977, 12, 307-312
· TodCon,
pages 85-86
· Trin,
page 229
1^Chi^v see 57.
Source:
· Kier,
L. B.; Hall L. H. Derivation and Significance of
· TodCon,
pages 85-86
· Trin,
page 229
2^Chi^v see 57.
3^Chi^v see 57.
1^kappa is a descriptor of the category 'topological'.
Notation in text: 
where is the number of atoms
and is the number of bonds
in an H-suppressed molecular graph.
Source:
· Kier,
L. B. Shape Indexes of Orders One and Three from Molecular Graphs. Quant. Struct.-Act. Relat. 1986, 5, 1-7
· Kier,
L. B. Indexes of Molecular Shape from Chemical Graphs. Acta Pharm. Jugosl. 1986,
36, 171-188
· TodCon, pages 248-249
2^kappa is a descriptor of the category 'topological'.
Notation in text: 
where is the number of atoms
and 
is the number of paths
of length 2 in an H-suppressed molecular graph.
For see 0.
Source:
· Kier,
L. B. A Shape Index from Molecular Graphs. Quant.
Struct.-Act. Relat. 1985, 4, 109-116
· Kier,
L. B. Indexes of Molecular Shape from Chemical Graphs. Acta Pharm. Jugosl. 1986,
36, 171-188
· TodCon, pages 248-249
3^kappa is a descriptor of the category 'topological'.
Notation in text: 
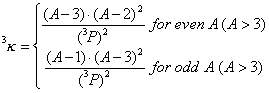
where is the number of atoms
and 
is the number of paths
of length 3 in an H-suppressed molecular graph.
For see 0.
Source:
· Kier,
L. B. Shape Indexes of Orders One and Three from Molecular Graphs. Quant. Struct.-Act. Relat. 1986, 5, 1-7
· Kier,
L. B. Indexes of Molecular Shape from Chemical Graphs. Acta Pharm. Jugosl. 1986,
36, 171-188
· TodCon, pages 248-249
Phi_non-alpha is a descriptor of the category 'topological'.
Notation in text: 
where is the number of
atoms. , are the Kier shape
indices 1 and 2.
For and see 61 and 62.
For see 0.
Source:
·
No source! Definition is analogous to 68 without modifying alpha.
1^kappa_alpha is a descriptor of the category 'topological'.
Notation in text: 
where is the number of atoms
and is the number of bonds
in an H-suppressed molecular graph. 
is derived from the
covalent radius of each atom.
For see alpha.
For see 0. For see 22.
Source:
· Kier, L. B. Distinguishing Atom Differences in a Molecular Graph Shape Index. Quant. Struct.-Act. Relat. 1986, 5, 7-12
· Kier,
L. B. Shape Indexes of Orders One and Three from Molecular Graphs. Quant. Struct.-Act. Relat. 1986, 5, 1-7
· Kier,
L. B. Indexes of Molecular Shape from Chemical Graphs. Acta Pharm. Jugosl. 1986,
36, 171-188
· TodCon, pages 249-250
2^kappa_alpha is a descriptor of the category 'topological'.
Notation in text: 
where is the number of atoms
and is the number of paths
of length 2 in an H-suppressed molecular graph. is derived from the
covalent radius of each atom.
Source:
· Kier, L. B. Distinguishing Atom Differences in a Molecular Graph Shape Index. Quant. Struct.-Act. Relat. 1986, 5, 7-12
· Kier,
L. B. Indexes of Molecular Shape from Chemical Graphs. Acta Pharm. Jugosl. 1986,
36, 171-188
· TodCon, pages 249-250
3^kappa_alpha is a descriptor of the category 'topological'.
Notation in text: 
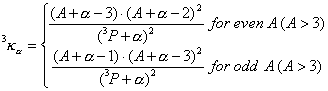
where is the number of atoms
and is the number of paths
of length 3 in an H-suppressed molecular graph. is derived from the
covalent radius of each atom.
Source:
· Kier,
L. B. Shape Indexes of Orders One and Three from Molecular Graphs. Quant. Struct.-Act. Relat. 1986, 5, 1-7
· Kier,
L. B. Indexes of Molecular Shape from Chemical Graphs. Acta Pharm. Jugosl. 1986,
36, 171-188
· TodCon, pages 249-250
Phi is a descriptor of the category 'topological'.
Notation in text: 
where is the number of
atoms. 
, are the Kier alpha-modified
shape indices 1 and 2. is derived from the
covalent radius of each atom.
For and see 65 and 66. For see 0.
Source:
· Kier,
L. B. An Index of Molecular Flexibility from Kappa Shape Attributes. Quant. Struct.-Act. Relat. 1989, 8, 221-224
· TodCon, page 178
F is a descriptor of the category 'topological'.
Notation in text: 
where 
is the number of
neighbours of atom i. The sum runs over all edges in an H-suppressed molecular
graph.
Source:
· Platt, J. R. Influence of Neighbor Bonds on Additive Bond Properties in Paraffins. J. Chem. Phys. 1947, 15, 419-420
· Platt,
J. R. Prediction of Isomeric Differences in Paraffin Properties. J. Phys. Chem. 1952, 56, 328-336
· TodCon, page 125
· Trin,
page 245
N_GS is a descriptor of the category 'topological'.
Notation in text: 
is the number of path
subgraphs of length 2 in an H-suppressed molecular graph.
Source:
· TodCon, page 125
· Trin,
245
J is a descriptor of the category 'topological'.
Notation in text: 
where is the number of bonds
and is the cyclomatic
number. 
is the ith
vertex distance degree. The sum runs over all edges of an H-suppressed
molecular graph.
For see 22. For see 39. For see vertex distance degree.
Source:
· Balaban,
A. T. Highly Discriminating Distance-Based Topological Index. Chem. Phys. Lett. 1982, 89, 399-404
· Balaban, A. T. Topological Indices Based on Topological Distances in Molecular Graphs. Pure Appl. Chem. 1983, 55, 199-206
· TodCon, page 21
· Trin,
page 246
J_unsat is a descriptor of the category 'topological'.
Notation in text: 
where is the number of bonds
and is the cyclomatic
number. 
is the ith
vertex unsaturated distance degree, i.e. the row sum in the unsaturated
distance matrix.
For see 22. For see 39. For see vertex unsaturated distance degree.
Source:
· Balaban,
A. T. Highly Discriminating Distance-Based Topological Index. Chem. Phys. Lett. 1982, 89, 399-404
· Balaban,
A. T.; Filip, P. Computer Program For Topological Index J. MATCH – Commun. Math. Comp. Chem. 1984, 16, 163
MTI is descriptor of the category 'topological'.
Notation in text: 
is defined for an H-suppressed
molecular graph:
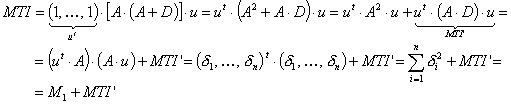
where is the adjacence
matrix (here not the descriptor : number of atoms), 
is the distance
matrix, 
the number of atoms, 
the second descriptor , 
is the vertex degree
of the ith atom and is the first Zagreb
index. The letter 
specifies the transposition
of a vector or a matrix: 
in a symmetric matrix.
For see adjacence matrix, for see distance matrix, for see 74, for see vertex degree, for see 45.
Source:
· Schultz,
H. P. Topological Organic Chemistry. 1. Graph Theory and Topological Indices of
Alkanes. J. Chem. Inf. Comput. Sci. 1989, 29, 227-228
· Schultz, H. P.; Schultz, T. P. Topological Organic Chemistry. 6. Graph Theory and Molecular Topological Indices of Cycloalkanes. J. Chem. Inf. Comput. Sci. 1993, 33, 240-244
· TodCon, page 381 (The formula given there is incorrect.)
· Trin,
page 257
MTI' is a descriptor of the category 'topological'.
Notation in text:
is defined for an H-suppressed
molecular graph:
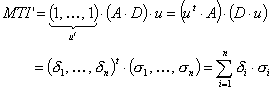
where is the adjacence
matrix (here not the descriptor : number of atoms), is the distance
matrix, the number of atoms, is the vertex degree
of the ith atom, is the vertex distance
degree of the ith atom. The letter specifies the transposition
of a vector or a matrix: in a symmetric matrix.
For see adjacency matrix, for see distance matrix, for see vertex degree and for see vertex distance degree.
Source:
· Müller, W. R.; Szymanski, K.; Knop, J. v.; Trinajstić, N. Molecular Topological Indices. J. Chem. Inf. Comput. Sci. 1990, 30, 160-163
· Mihalić, Z.; Nikolić, S; Trinajstić, N. Comparative Study of Molecular Descriptors Derived from the Distance Matrix. J. Chem. Inf. Comput. Sci. 1992, 32, 28-37
· TodCon,
page 381
H is a descriptor of the category 'topological'.
Notation in text: 
The sums run over all pairs of atoms in an H-suppressed molecular graph:
where is the number of non-H
atoms and is the entry in the ith
row and the jth column of the distance matrix.
For see 0 and for see distance matrix.
Source:
· Ivanciuc, O.; Balaban, T.-S.; Balaban, A. T. Design of Topological Indices. Part 4. Reciprocal Distance Matrix, Related Local Vertex Invariants and Topological Indices. J. Math. Chem. 1993, 12, 309-318
· Plavsić, D.; Nikolić, S; Trinajstić, N.; Mihalić, Z. On the Harary Index for the Characterization of Chemical Graphs. J. Math. Chem. 1993, 12, 235-250
· Lucić, B.; Milicević, A.; Nikolić, S; Trinajstić, N. Harary Index – Twelve Years Later. Croat. Chem. Acta 2002, 75, 847-867
· TodCon,
pages 209-210
twc is a descriptor of the category 'topological'.
Notation in text: 
The sum runs over all lengths (from length 
to length 
) of walks in an H-suppressed molecular graph:
where is the number of atoms
and 
is the molecular walk
count of length k.
For see 77-83.
Source:
· Rücker, G.; Rücker, C. Counts of All Walks as Atomic and Molecular Descriptors. J. Chem. Inf. Comput. Sci. 1993, 33, 683-695
· Rücker, G.; Rücker, C. Walk Counts, Labyrinthicity, and Complexity of Acyclic and Cyclic Graphs and Molecules. J. Chem. Inf. Comput. Sci. 2000, 40, 99-106
· Gutman,
· Nikolić,
S; Trinajstić, N.; Tolić,
· TodCon,
pages 480-482
mwc2, mwc3, mwc4, mwc5, mwc6, mwc7 and mwc8 are descriptors of the category 'topological'.
Notation in text: ; e.g.: 
The sums run over all atoms in an H-suppressed molecular graph:
where 
is the kth power
of the adjacency matrix (here not the
descriptor : number of atoms) and the number of atoms.
Remark: 
is equal to the number
of atoms, 
is equal to 
.
For see adjacency matrix, for see 22.
Source:
· Rücker, G.; Rücker, C. Counts of All Walks as Atomic and Molecular Descriptors. J. Chem. Inf. Comput. Sci. 1993, 33, 683-695
· Rücker, G.; Rücker, C. Walk Counts, Labyrinthicity, and Complexity of Acyclic and Cyclic Graphs and Molecules. J. Chem. Inf. Comput. Sci. 2000, 40, 99-106
· Gutman, I.; Rücker, C.; Rücker, G. On Walks in Molecular Graphs J. Chem. Inf. Comput. Sci. 2001, 41, 739-745
· Nikolić,
S; Trinajstić, N.; Tolić,
· TodCon,
pages 480-482
twc_unsat is a descriptor of the category 'topological'.
Notation in text: 
The sum runs over all lengths (from length to length ) of walks in an H-suppressed molecular graph:
where is the number of atoms
and 
is the molecular walk
count of length 
derived from the “unsaturated”
adjacency matrix, i. e. a matrix with entries 
for multiple bonds.
For see 85-91. See also unsaturated adjacency matrix.
Source:
· No
source. Definition is analogous to 76.
mwc2_unsat, mwc3_unsat, mwc4_unsat, mwc5_unsat, mwc6_unsat, mwc7_unsat and mwc8_unsat are descriptors of the category 'topological'.
Notation in text: ; e.g.: 
The sums run over all atoms in an H-suppressed molecular graph:
where 
is the kth power
of the unsaturated adjacency matrix 
with entries for multiple bonds, and
is the number of
atoms.
For see unsaturated adjacency matrix, for see 22.
Source:
· No
source. Definition is analogous to 77-83.
G_1 (topo. dist.) is a descriptor of the category 'topological'.
Notation in text: 
The sum runs over all pairs of atoms in an H-suppressed molecular graph.
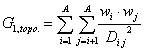
where 
is the average weight
of atom i (expressed in amu, i.e. 12.0110
for carbon) and is the entry in the ith
row and the jth column of the distance matrix. is the number of
atoms.
For see distance matrix. For see 0.
Source:
· No
source. Definition is analogous to 96 with topological
distances.
G_1 (topo. dist.,incl. H) is a descriptor of the category 'topological'.
Notation in text: 
The sum runs over all pairs of atoms in a molecular graph containing H atoms.
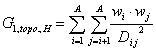
where is the average weight
of atom i and is the entry in the ith
row and the jth column of the distance matrix. is the number of
atoms.
For see distance matrix. For see 0.
Source:
· No
source. Definition is analogous to 97 with topological
distances.
G_2 (topo. dist.) is a descriptor of the category 'topological'.
Notation in text: 
The sum runs over all edges of an H-suppressed molecular graph.
where is the average weight
of atom 
.
Source:
· No
source. Definition is analogous to 98 with topological
distances.
G_2 (topo. dist.,incl. H) is a descriptor of the category 'topological'.
Notation in text: 
The sum runs over all edges of a molecular graph containing H atoms.
where is the average weight
of atom .
· No
source. Definition is analogous to 99 with topological
distances.
G_1 is a descriptor of the category 'geometrical'.
The sum runs over all pairs of an H-suppressed molecular graph.
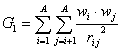
where is the average weight
of atom and 
is the interatomic
distance (expressed in Ångström Å) of atom i and atom j. is the number of
atoms.
For see 0.
Source:
· Katritzky,
A. R.; Mu L.; Lobanov, V. S.; Karelson, M. Correlation of Boiling Points with
Molecular Structure. 1. A Training Set of 298 Diverse Organics and a Test Set
of 9 Simple Inorganics. J. Phys. Chem.
1996, 100, 10400-10407
· TodCon,
page 412
G_1 (incl. H) is a descriptor of the category 'geometrical'.
The sum runs over all pairs of atoms in a molecular graph containing H atoms.
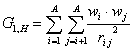
where is the average weight
of atom and is the interatomic
distance (expressed in Ångström Å) of atom i and atom j. is the number of
atoms.
For see 0.
Source:
· Katritzky,
A. R.; Mu L.; Lobanov, V. S.; Karelson, M. Correlation of Boiling Points with
Molecular Structure. 1. A Training Set of 298 Diverse Organics and a Test Set
of 9 Simple Inorganics. J. Phys. Chem.
1996, 100, 10400-10407
· TodCon,
page 412
G_2 is a descriptor of the category 'geometrical'.
The sum runs over all edges of an H-suppressed molecular graph.
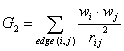
where is the average weight
of atom and is the interatomic
distance (expressed in Ångström Å) of atom i and atom j.
Source:
· Katritzky,
A. R.; Mu L.; Lobanov, V. S.; Karelson, M. Correlation of Boiling Points with
Molecular Structure. 1. A Training Set of 298 Diverse Organics and a Test Set
of 9 Simple Inorganics. J. Phys. Chem.
1996, 100, 10400-10407
· TodCon,
page 412
G_2 (incl. H) is a descriptor of the category 'geometrical'.
Notation in text: 
The sum runs over all edges of a molecular graph containing H atoms.
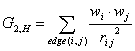
where is the average weight
of atom and is the interatomic
distance (expressed in Ångström Å) of atom i and atom j.
Source:
· Katritzky,
A. R.; Mu L.; Lobanov, V. S.; Karelson, M. Correlation of Boiling Points with
Molecular Structure. 1. A Training Set of 298 Diverse Organics and a Test Set
of 9 Simple Inorganics. J. Phys. Chem.
1996, 100, 10400-10407
· TodCon,
page 412
Z is a descriptor of the category 'topological'.
Notation in text: 
where is the number of atoms
in the H-suppressed molecular graph and 
is the number of sets
of mutually non-adjacent
edges. 
, 
.
Source:
· Hosoya,
H. Topological Index. A Newly Proposed Quantity Characterizing the Topological
Nature of Structural Isomers of Saturated Hydrocarbons. Bull. Chem. Soc. Jpn. 1971,
44, 2332-2339
· TodCon, page 215
· Trin,
page 132
IC_0, IC_1, IC_2, TIC_0, TIC_1, TIC_2, CIC_0, CIC_1, CIC_2, N*CIC_0, N*CIC_1, N*CIC_2, SIC_0, SIC_1, SIC_2, N*SIC_0, N*SIC_1, N*SIC_2, BIC_0, BIC_1, BIC_2, N*BIC_0, N*BIC_1 and N*BIC_2 are descriptors of the category 'topological'.
Notation in text: 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
For calculating these descriptors a molecular graph inclusive H atoms is considered.
Explanation:
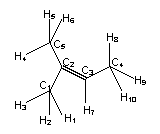Every
atom is characterized by itself and its neighbours. Here the characterization
of the ith atom itself depends on the atom number 
and on the number of
bonding electron pairs (without H atoms). The
characterization of the neighbourhood depends on the depth 
of the neighbourhood
(e.g. 
for the next
neighbours) and the characterization of the connected atoms and their bond multiplicities:
To calculate only the
characterization of the atoms is needed: C1, C2, C3,
C4, C5 are C-atoms and have all
with 
is the number of atoms
and 
is the number of
bonds.
Source:
·
Basak, S. C. Information Theoretic Indices of
Neighborhood Complexity and Their Applications, chapter 12 in Topological Indices and Related Descripors
in QSAR and QSPR (Devillers, J.; Balaban, A. T., Eds.) Gordon and Breach,
· Basak, S. C. Use of Molecular Complexity Indices in Predictive Pharmacology and Toxicology: A QSAR Approach. Med. Sci. Res. 1987, 15, 605-609
·
Basak, S. C.; Gute, B. D. Characterization of Molecular
Structures Using Topological Indices. SAR
QSAR Environ. Res. 1997, 7, 1-21
TIC_0 see 101.
CIC_0 see 101.
N*CIC_0 see 101.
SIC_0 see 101.
N*SIC_0 see 101.
BIC_0 see 101.
N*BIC_0 see 101.
IC_1 see 101.
TIC_1 see 101.
CIC_1 see 101.
N*CIC_1 see 101.
SIC_1 see 101.
N*SIC_1 see 101.
BIC_1 see 101.
N*BIC_1 see 101.
IC_2 see 101.
TIC_2 see 101.
CIC_2 see 101.
N*CIC_2 see 101.
SIC_2 see 101.
N*SIC_2 see 101.
BIC_2 see 101.
N*BIC_2 see 101.
MSD is a descriptor of the category 'topological'.
Notation in text: 
The sums run over all atoms of an H-suppressed molecular graph:
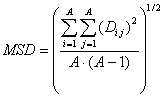
where is the number of non-H
atoms and is the entry in the ith
row and the jth column of the distance matrix.
For see 0 and for see distance matrix.
Source:
· Balaban,
A. T. Topological Indices Based on Topological Distances in Molecular Graphs. Pure Appl. Chem. 1983, 55, 199-206
· TodCon,
page 113 (The formula given there is incorrect.)
w is a descriptor of the category 'topological'.
Notation in text: 
The sums run over all atoms of an H-suppressed molecular graph:
where is the number of non-H
atoms and 
is the entry in the ith
row and the jth column of the detour matrix.
For see 0 and for see detour matrix.
Source:
·
Ivanciuc, O.; Balaban, A. T. Design of Topological
Indices. Part 8. Path Matrices and Derived Molecular Graph Invariants. MATCH – Commun. Math. Comp. Chem. 1994, 30, 141-152
· Amić, D.; Trinajstić, N. On the Detour Matrix. Croat. Chem. Acta. 1995, 68, 53-62
· Lukovits, I. The Detour Index. Croat. Chem. Acta 1996, 69, 873-882
· Lukovits,
· TodCon, page 103
w (incl. half diag.) is a descriptor of the category 'topological'.
Notation in text: 
The sums run over all atoms of an H-suppressed molecular graph:
where is the number of non-H
atoms and 
is the entry in the ith
row and the jth column of the detour matrix containing diagonal
elements 
.
For see 0 and for see detour matrix.
Source:
Rücker, G.; Rücker, C. Symmetry-Aided Computation of the Detour Matrix and the Detour Index. J. Chem. Inf. Comput. Sci. 1998, 38, 710-714
P_acyc, 2^P_acyc, 3^P_acyc, 4^P_acyc, 5^P_acyc, 6^P_acyc, 7^P_acyc, 8^P_acyc, 9^P_acyc and higher are descriptors of the category 'topological'.
Notation in text: 
, 
, 
, 
, 
, 
, 
, 
, 
where 
is the number of paths
of length 
in the H-suppressed molecular
graph without counting any closed paths (rings). 
is the maximum length
of all unclosed paths.
Source:
· Randić, M.; Brissey, G. M.; Spencer, R. B.; Wilkins, C. L. Search for All Self-Avoiding Paths for Molecular Graphs. Comput. & Chem. 1979, 3, 5-13
· Randić, M. Characterization of Atoms, Molecules, and Classes of Molecules Based on Paths Enumeration. MATCH – Commun. Math. Comp. Chem. 1979, 7, 5-64
· TodCon,
page 344
9^P_acyc and higher see
128-135.
P, 2^P, 3^P, 4^P, 5^P, 6^P, 7^P, 8^P, 9^P and higher are descriptors of the category 'topological'.
Notation in text: 
, 
, 
, 
, 
, 
, 
, 
, 
where 
is the number of paths
of length in the H-suppressed
molecular graph including closed paths (rings). is the maximum length
of all paths.
Source:
· Randić, M.; Brissey, G. M.; Spencer, R. B.; Wilkins, C. L. Search for All Self-Avoiding Paths for Molecular Graphs. Comput. & Chem. 1979, 3, 5-13
· Randić, M. Characterization of Atoms, Molecules, and Classes of Molecules Based on Paths Enumeration. MATCH – Commun. Math. Comp. Chem. 1979, 7, 5-64
· TodCon,
page 344
9^P and higher see
137-144.
rings, 3^rings, 4^rings, 5^rings, 6^rings, 7^rings, 8^rings, 9^rings and higher are descriptors of the category 'topological'.
Notation in text: 
, 
, 
, 
, 
, 
, 
, 
where 
is the number of rings
of length (size) in the H-suppressed molecular
graph. is the maximum size of
all rings.
Source:
· TodCon,
page 94
9^rings and higher see
146-152.
I_A, I_B, I_C are
descriptors of the category 'geometrical'.
Notation in text: 
, 
, 
, and are the three
principal moments of inertia of the molecule with 
.
Source:
· TodCon,
page 352
I_B see 154.
I_C see 154.
ch. G_1, ch. G_2, ch. G_3, ch. G_4, ch. G_5, ch. G_6, ch. G_7, ch. G_8 are descriptors of the category 'topological’.
Notation in text: 
, 
, 
, 
, 
, 
, 
, 
The sums run over all atoms in an H-suppressed molecular graph.
where 
is the charge term
matrix, is the number of
atoms, is the distance from
atom to atom 
, 
, and 
is the Kronecker delta:
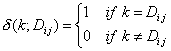
For see 0, for see distanc matrix, for see charge term matrix.
Source:
· Gálvez,
J.; Garcìa, R.; Salabert, M. T.; Soler, R. Charge Indexes. New Topologcal
Descriptors. J. Chem. Inf. Comput. Sci.
1994, 34, 520-525
· Gálvez
, J.; Garcìa-Domenech, R.; De Julián-Ortiz, V.; Soler, R. Topological Approach
to Drug Design. J. Chem. Inf. Comput.
Sci. 1995, 35, 272-284
· TodCon, pages 445-446
ch. J_1, ch. J_2, ch. J_3, ch. J_4, ch. J_5, ch. J_6, ch. J_7, ch. J_8 and ch. J [5] are descriptors of the category 'topological'.
Notation in text: 
, 
, 
, 
, 
, 
, 
, 
, 
, mean topological charge index
, global topological charge index
where is the number of atoms,
, and 
is the topological
charge index of order .
Source:
· Gálvez,
J.; Garcìa, R.; Salabert, M. T.; Soler, R. Charge Indexes. New Topologcal
Descriptors. J. Chem. Inf. Comput. Sci.
1994, 34, 520-525
· Gálvez
, J.; Garcìa-Domenech, R.; De Julián-Ortiz, V.; Soler, R. Topological Approach
to Drug Design. J. Chem. Inf. Comput.
Sci. 1995, 35, 272-284
· TodCon, pages 445-446
ch. J [5] see 165-172.
slog P is a descriptor of the category 'miscellaneous'.
Notation in text: 
where 
is the number of atoms
of Crippen type , is an increment for
the hydrophobicity of atom type . Structure-based types are attributed to atoms using a
special table.
Source:
· Wildman,
S. A.; Crippen, G. M. Prediction of Physicochemical Parameters by Atomic
Contributions J. Chem. Inf. Comput. Sci.
1999, 39, 868-873
sMR is a desriptor of the category 'miscellaneous'.
Notation in text: 
where is the number of atoms
of Crippen type , is an increment for
the molar refractivity of atom type . Structure-based types are attributed to atoms using a
special table.
Source:
· Wildman,
S. A.; Crippen, G. M. Prediction of Physicochemical Parameters by Atomic
Contributions J. Chem. Inf. Comput. Sci.
1999, 39, 868-873
st. energy is a descriptor of the category 'geometrical'.
Notation in text: 
This is the steric energy, as calculated by molecular
mechanics in MOLGEN.
D is a descriptor of the category 'topological'.
Notation in text:
is the short name of the topological diameter:
where is the number of atoms
in the H-suppressed molecular graph and 
is an entry in the
distance matrix.
For see 0 and for see distance matrix.
Source:
· TodCon,
page 112
at C01- at C27, at H01- at H04, at O01- at O12, at N01- at N14, at Hal, at Cl, at Br, at I, at F, at P, at S01- at S03, at Me01, at Me02 are descriptors of the category 'miscellaneous'.
Notation in text: 
, 
, …, 
, …, 
Source:
· Wildman,
S. ; Crippen, G. M. A. Prediction of Physicochemical Parameters by Atomic
Contributions J. Chem. Inf. Comput. Sci.
1999, 39, 868-873
0-8^K is a descriptor of the category 'overall'.
Notation in text: 
where 
is the number of
subgraphs of edges.
For see 247-255.
Source:
· Bonchev, D. Novel Indices for the Topological Complexity of Molecules. SAR QSAR Environ. Res. 1997, 7, 23-43
· Rücker,
G.; Rücker, C. Automatic Enumeration of All Connected Subgraphs. MATCH – Commun. Math. Comp. Chem. 2000, 41, 145-149
0^K, 1^K, 2^K, 3^K, 4^K, 5^K, 6^K, 7^K and 8^K are descriptors of the category 'overall'.
Notation in text: 
, 
, …, 
where 
is the H-suppressed molecular
graph.
Source:
· Bonchev, D. Novel Indices for the Topological Complexity of Molecules. SAR QSAR Environ. Res. 1997, 7, 23-43
· Rücker,
G.; Rücker, C. Automatic Enumeration of All Connected Subgraphs. MATCH – Commun. Math. Comp. Chem. 2000, 41, 145-149
Xi^c is a descriptor of the category 'topological'.
Notation in text: 
where 
is the maximum entry
in the ith line of the distance matrix. is the vertex degree
of atom .
For see vertex degree, for see eccentricity.
Source:
· Sharma,
V.; Goswami, R.; Madan, A. K. Eccentric Conectivity Index: A Novel Highly
Discriminating Topological Descriptor for Structure-Property and
Structure-Activity Studies J. Chem. Inf.
Comput. Sci. 1997, 37, 273-282
· TodCon, page 124
lambda_1^A is a descriptor of the category 'topological'.
Notation in text: 
is the principal
eigenvalue of the adjacency matrix .
For see adjacency matrix.
Source:
· TodCon,
page 131
SCA1, SCA2 and SCA3 are descriptors of the category 'topological'.
Notation in text: 
, 
, 
The sum runs over all atoms of an H-suppressed molecule:
where is the number of
atoms, 
is the ith
coefficient of the eigenvector of the principal eigenvalue of . All coefficients in a principle eigenvector have the same
sign, here always the positive sign is assumed.
The descriptors SCR2 and SCR3 are calculated analogously to VEA in TodCon, page 132.
For see adjacency matrix.
Source:
· Rücker,
G.; Rücker, C.; Gutman, I. On Kites, Comets, and Stars. Sums of Eigenvector
Coefficients in (Molecular) Graphs. Z. Naturforsch.
A 2002, 57a, 143-153
SCA2 see SCA1.
SCA3 see SCA1.
lambda_1^D is descriptor of the category 'topological'.
Notation in text: 
is the principal
eigenvalue of the distance matrix .
For see distance matrix.
Source:
· Schultz,
H. P.; Schultz, E. B.; Schultz, T. P. Topological Organic Chemistry. 2. Graph
Theory, Matrix Determinants and Eigenvalues, and Topological Indices of
Alkanes. J. Chem. Inf. Comput. Sci. 1990, 30, 27-29
· TodCon,
page 134
cha is a descriptor of the category 'arithmetic'.
Notation in text: 
is the charge of the
molecule.
n_rad is a descriptor of the category 'arithmetic'.
Notation in text: 
is the number of
radical sites in a molecule.
Chi_T is a descriptor of the category 'topological'.
Notation in text: 
The product runs over all atoms of an H-suppressed molecular graph.
where is the vertex degree
of atom . is the number of atoms.
For see vertex degree, for see 0.
Source:
·
· TodCon,
page 86
T_m is a descriptor of the category 'topological'.
Notation in text: 
is the number of
methyl groups in a molecular graph with H atoms.
Source:
·
T_3 is a descriptor of the category 'topological'.
Notation in text: 
is the number of pairs
of methyl groups at distance 3.
For see 0 and for see distance matrix.
Source:
·
HBD is a descriptor of the category 'arithmetic'.
Notation in text: 
is the number of H
atoms attached to O and N atoms, in accord with the ACD definition.
Source:
· STNotes 2002, 28, 3
· TodCon, page 221-222
HBA is a descriptor of the category 'arithmetic'.
Notation in text: 
is the number of N and
O atoms, in accord with the ACD definition.
Source:
· STNotes 2002, 28, 3
· TodCon, page 221-222
FRB is a descriptor of the category 'topological'.
Notation in text: 
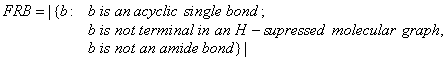
Source:
· Veber, D. F.; Johnson, S. R.; Cheng, H.-Y.; Smith, B. R.; Ward, K. W.; Kopple, K. D. Molecular Properties that Influence the Oral Bioavailability of Drug Candidates. J. Med. Chem. 2002, 45, 2615-2623
· TodCon,
page 178
SHDW1, SHDW2 , SHDW3, SHDW4, SHDW5, SHDW6, SHDW1/ SHDW2, SHDW1/ SHDW3, SHDW2/ SHDW3, ssSHDW1, ssSHDW2 , ssSHDW3, ssSHDW4, ssSHDW5, ssSHDW6, ssSHDW1/ SHDW2, ssSHDW1/ SHDW3, ssSHDW2/ SHDW3 are descriptors of the category 'geometrical'.
Notation in text: 
, 
, 
, …, 
, …, 
, 
where 
, 
and are the principle axes
of inertia of the molecule (incl. H atoms). Each atom is projected using its
vdw radius.
where 
, 
and 
are the maximum
dimension of the molecular surface in , and direction using vdw
radii.
Source:
· Jurs,
P. C.; Hasan, M. N.; Hansen, P. J.; Rohrbaugh, R. H. Prediction of Physicochemical
Properties of Organic Compounds from Molecular Structure, pages 209-233 in Physical Property Prediction (Jochum,
C., Ed.) Springer,
· Rohrbaugh, R. H.; Jurs, P. C. Description of Molecular Shape Applied in Studies of Structure/Activity and Structure/Property Relationships Anal. Chim. Acta 1987, 199, 99-109
· Rohrbaugh,
R. H.; Jurs, P. C. Molecular Shape and the Prediction of HPLC Retention Indexes
of Polycyclic Aromatic Hydrocarbons Anal.
Chem. 1987, 59, 1048-1054
· TodCon, page 389
where 
is the largest value, 
is the second largest value,
and 
is the smallest value
of 
. 
stands for
size-sorted.
, 
and 
span the respective
plane of projection.
Source:
· TodCon, page 389
SHDW2 see 270.
SHDW3 see 270.
SHDW4 see 270.
SHDW5 see 270.
SHDW6 see 270.
SHDW1/SHDW2 see 270.
SHDW1/SHDW3 see 270.
SHDW2/SHDW3 see 270.
ssSHDW1 see 270.
ssSHDW2 see 270.
ssSHDW3 see 270.
ssSHDW4 see 270.
ssSHDW5 see 270.
ssSHDW6 see 270.
ssSHDW1/SHDW2 see 270.
ssSHDW1/SHDW3 see 270.
ssSHDW2/SHDW3 see 270.
V_vdw, density_vdw, V_vdw^s, V_cub are descriptors of the category 'geometrical'.
Notation in text: 
, 
, 
, 
, , and are calculated for
molecules including H atoms.
where , and are the maximum
dimensions of the molecular surface in , and direction by using 
, where , and are the principle axes
of inertia of the molecule (incl. H atoms).
Source:
· TodCon, page 326
rho_vdw see 288.
V_vdw^s see 288.
V_cub see 288.
S(atomic subgraph) are descriptors of the category 'electrotopol./AI’;
e.g. S(sCH3) for subgraph: -CH3.
Notation in text: 
, …
is the sum of
electrotopological state values of all 
subgraphs.
The S(sCH3) is descriptor 292. Here is the list of all E-state descriptors from 292 to 371:
|
292 |
S(sCH3) |
312 |
S(sssNH) |
332 |
S(aaS) |
352 |
S(ssSiH2) |
|
293 |
S(dCH2) |
313 |
S(dsN) |
333 |
S(dssS) |
353 |
S(sssSiH) |
|
294 |
S(ssCH2) |
314 |
S(aaN) |
334 |
S(ddssS) |
354 |
S(ssssSi) |
|
295 |
S(tCH) |
315 |
S(sssN) |
335 |
S(ssssssS) |
355 |
S(sGeH3) |
|
296 |
S(dsCH) |
316 |
S(ddsN) |
336 |
S(sCl) |
356 |
S(ssGeH2) |
|
297 |
S(aaCH) |
317 |
S(aasN) |
337 |
S(sSeH) |
357 |
S(sssGeH) |
|
298 |
S(sssCH) |
318 |
S(ssssN) |
338 |
S(dSe) |
358 |
S(ssssGe) |
|
299 |
S(ddC) |
319 |
S(sOH) |
339 |
S(ssSe) |
359 |
S(sAsH2) |
|
300 |
S(tsC) |
320 |
S(dO) |
340 |
S(aaSe) |
360 |
S(ssAsH) |
|
301 |
S(dssC) |
321 |
S(ssO) |
341 |
S(dssSe) |
361 |
S(sssAs) |
|
302 |
S(aasC) |
322 |
S(aaO) |
342 |
S(ddssSe) |
362 |
S(sssdAs) |
|
303 |
S(aaaC) |
323 |
S(sF) |
343 |
S(sBr) |
363 |
S(sssssAs) |
|
304 |
S(ssssC) |
324 |
S(sPH2) |
344 |
S(sI) |
364 |
S(sSnH3) |
|
305 |
S(sNH3) |
325 |
S(ssPH) |
345 |
S(sLi) |
365 |
S(ssSnH2) |
|
306 |
S(sNH2) |
326 |
S(sssP) |
346 |
S(ssBe) |
366 |
S(sssSnH) |
|
307 |
S(ssNH2) |
327 |
S(dsssP) |
347 |
S(ssssBe) |
367 |
S(ssssSn) |
|
308 |
S(dNH) |
328 |
S(sssssP) |
348 |
S(ssBH) |
368 |
S(sPbH3) |
|
309 |
S(ssNH) |
329 |
S(sSH) |
349 |
S(sssB) |
369 |
S(ssPbH2) |
|
310 |
S(aaNH) |
330 |
S(dS) |
350 |
S(ssssB) |
370 |
S(sssPbH) |
|
311 |
S(tN) |
331 |
S(ssS) |
351 |
S(sSiH3) |
371 |
S(ssssPb) |
where s means a single bond, ss two single bonds, d a double bonds, t a triple bond, a an aromatic bond, etc. connected to the specified atom, not counting the single bonds to the attached H atoms. H2 means two attached H atoms.
Source:
· Kier,
L. B.; Hall, L. H. Molecular Structure
Description. The
SZD, SZDp are indices of the category 'topological'.
Notation in text: 
, 
The sums run over an H-suppressed molecular graph:
where is the number of atoms
in the H-suppressed molecular graph and 
is the
For see 0 and for see Szeged matrix.
Source:
· Khadikar,
P. V.; Deshpande, N.V.; Kale, P. P.; Dobrynin, A.; Gutman, I.; Dömötör, G. The
· Gutman,
I; Klavzar, S. An Algorithm for the Calculation of the
· Zerovnik,
J. Computing the
· Zerovnik,
J. Szeged Index of Symmetric Graphs. J.
Chem. Inf. Comput. Sci. 1999, 39, 77-80
· TodCon,
page 438
SZDp see 372.
S_vdw is a descriptor of the category 'geometrical'.
Notation in text: 
is the surface of the
molecule by using vdw radii for each atom.
SASA H2O is a descriptor of the category 'geometrical'.
Notation in text: 
is the solvent
accessible surface of the molecule by using vdw radii and an H2O
molecule (r = 1.5Å) as a probe.
SASA H is a descriptor of the category 'geometrical'.
Notation in text: 
is the solvent
accessible surface of the molecule by using vdw radii and an H atom (r = 1.2Å)
as a probe.
AI(atomic subgraph) are descriptors of the category 'electrotopol./AI’;
eg. AI(sCH3) for subgraph: -CH3.
Notation in text: 
, …
The sums run over an H-suppressed molecular graph:
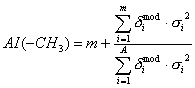
where is the number of 
subgraphs, 
(or 
) is the modified vertex degree of atom and 
is the vertex distance
degree of atom .
For the subgraphs considered see 292-371, for see modified vertex degree and for see vertex distance degree.
The AI(sCH3) is descriptor 377. Here is the list of all AI descriptors from 377 to 456:
|
377 |
AI(sCH3) |
397 |
AI(sssNH) |
417 |
AI(aaS) |
437 |
AI(ssSiH2) |
|
378 |
AI(dCH2) |
398 |
AI(dsN) |
418 |
AI(dssS) |
438 |
AI(sssSiH) |
|
379 |
AI(ssCH2) |
399 |
AI(aaN) |
419 |
AI(ddssS) |
439 |
AI(ssssSi) |
|
380 |
AI(tCH) |
400 |
AI(sssN) |
420 |
AI(ssssssS) |
440 |
AI(sGeH3) |
|
381 |
AI(dsCH) |
401 |
AI(ddsN) |
421 |
AI(sCl) |
441 |
AI(ssGeH2) |
|
382 |
AI(aaCH) |
402 |
AI(aasN) |
422 |
AI(sSeH) |
442 |
AI(sssGeH) |
|
383 |
AI(sssCH) |
403 |
AI(ssssN) |
423 |
AI(dSe) |
443 |
AI(ssssGe) |
|
384 |
AI(ddC) |
404 |
AI(sOH) |
424 |
AI(ssSe) |
444 |
AI(sAsH2) |
|
385 |
AI(tsC) |
405 |
AI(dO) |
425 |
AI(aaSe) |
445 |
AI(ssAsH) |
|
386 |
AI(dssC) |
406 |
AI(ssO) |
426 |
AI(dssSe) |
446 |
AI(sssAs) |
|
387 |
AI(aasC) |
407 |
AI(aaO) |
427 |
AI(ddssSe) |
447 |
AI(sssdAs) |
|
388 |
AI(aaaC) |
408 |
AI(sF) |
428 |
AI(sBr) |
448 |
AI(sssssAs) |
|
389 |
AI(ssssC) |
409 |
AI(sPH2) |
429 |
AI(sI) |
449 |
AI(sSnH3) |
|
390 |
AI(sNH3) |
410 |
AI(ssPH) |
430 |
AI(sLi) |
450 |
AI(ssSnH2) |
|
391 |
AI(sNH2) |
411 |
AI(sssP) |
431 |
AI(ssBe) |
451 |
AI(sssSnH) |
|
392 |
AI(ssNH2) |
412 |
AI(dsssP) |
432 |
AI(ssssBe) |
452 |
AI(ssssSn) |
|
393 |
AI(dNH) |
413 |
AI(sssssP) |
433 |
AI(ssBH) |
453 |
AI(sPbH3) |
|
394 |
AI(ssNH) |
414 |
AI(sSH) |
434 |
AI(sssB) |
454 |
AI(ssPbH2) |
|
395 |
AI(aaNH) |
415 |
AI(dS) |
435 |
AI(ssssB) |
455 |
AI(sssPbH) |
|
396 |
AI(tN) |
416 |
AI(ssS) |
436 |
AI(sSiH3) |
456 |
AI(ssssPb) |
where s means a single bond, ss two single bonds, d a double bonds, t a triple bond, a an aromatic bond, etc. connected to the specified atom not counting the single bonds to the attached H atoms. H2 means two attached H atoms.
Source:
· Ren, B. Novel Atomic-Level-Based AI Topological Descriptors: Application to QSPR/QSAR Modeling. J. Chem. Inf. Comput. Sci. 2002, 42, 858-868
· Ren, B. Novel Atomic-Level-Based AI Topological Descriptors for Structure-Property Correlations. J. Chem. Inf. Comput. Sci. 2003, 43, 161-169
· Ren, B. Novel Atom-Type AI Indices for QSPR Studies of Alcohols. Comput. & Chem. 2002, 26, 223-235
· Ren, B. Application of Novel Atom-Type AI Topological Indices to QSPR Studies of Alkanes. Comput. & Chem. 2002, 26, 357-369
Xu, Xu^m are descriptors of the category 'electrotopol./AI'.
Notation in text: 
, 
The sum runs over all atoms of an H-suppressed molecule:
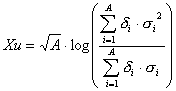
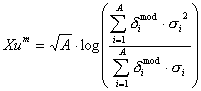
where is the number of atoms
in an H-suppressed molecule, is the vertex degree
of the ith atom, is the vertex distance
degree of the ith atom. (or ) is the modified vertex degree of atom .
For see 0, for see vertex degree, for see vertex distance degree and for see modified vertex degree.
Source:
· Ren,
B. A New Topological Index for QSPR of Alkanes. J. Chem. Inf. Comput. Sci. 1999,
39, 139-143
· TodCon, page 507
Xu^m see 457.
m^Chi_q and m^Chi^v_q are descriptors of the category 'topological'. Substructures are paths, clusters, path-clusters and chains.
Available are:
|
459 |
3^Chi_p |
469 |
6^Chi_pc |
479 |
4^Chi^v_c |
|
460 |
4^Chi_p |
470 |
3^Chi_ch |
480 |
5^Chi^v_c |
|
461 |
5^Chi_p |
471 |
4^Chi_ch |
481 |
6^Chi^v_c |
|
462 |
6^Chi_p |
472 |
5^Chi_ch |
482 |
4^Chi^v_pc |
|
463 |
3^Chi_c |
473 |
6^Chi_ch |
483 |
5^Chi^v_pc |
|
464 |
4^Chi_c |
474 |
3^Chi^v_p |
484 |
6^Chi^v_pc |
|
465 |
5^Chi_c |
475 |
4^Chi^v_p |
485 |
3^Chi^v_ch |
|
466 |
6^Chi_c |
476 |
5^Chi^v_p |
486 |
4^Chi^v_ch |
|
467 |
4^Chi_pc |
477 |
6^Chi^v_p |
487 |
5^Chi^v_ch |
|
468 |
5^Chi_pc |
478 |
3^Chi^v_c |
488 |
6^Chi^v_ch |
Notation in text: 
, 
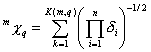
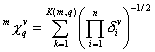
where is the vertex degree
and is the valence vertex
degree of atom of the subgraph of
type 
in the H-suppressed
molecular graph. is the order (this is also
called the “size” or “the number of edges”) of the subgraphs considered. means paths, clusters,
path-clusters or chains. 
is the number of subgraphs
of type and size . is the number of atoms
of the subgraph considered.
Type of subgraphs:
· If
a subgraph contains a cycle it is of type chain (
) for 
,
· otherwise
if every vertex has one or more than two non-H neighbours it is of type cluster
() for ,
· otherwise
if every vertex has one or two non-H neighbours it is of type path () for 
,
· otherwise
it is of type path-cluster (
) for 
. So a path-cluster has no cycles but vertices with one, two
and more than two non-H neighbours.
For example paths are:
|
path |
|
|
|
|
|
3 |
4 |
5 |
For example chains are:
|
chain |
|
|
|
|
|
3 |
4 |
4 |
For example clusters are:
|
cluster |
|
|
|
|
|
3 |
4 |
5 |
For example path-clusters are:
|
path-cluster |
|
|
|
|
|
4 |
6 |
6 |
For see vertex degree, for see valence vertex degree.
Source:
· Kier, L. B.; Hall L. H. The Nature of Structure-Acticity Relationships and their Relation to Molecular Connectivity. Eur. J. Med. Chem., 1977, 12, 307-312
· Kier,
L. B.; Hall L. H. Molecular Connectivity
in Structure-Activity Analysis. Research Studies Press - Wiley,
· TodCon, pages 84-86 and page 314
m^TO, m^TO*, m^TO_q, m^TO*_q, TO, TO*, TO_q, TO*_q are descriptors of the category 'overall'.
Available are:
|
489 |
0^TC
|
542 |
2^TW
|
595 |
5^TC*_c
|
648 |
4^TM_2_pc
|
|
490 |
1^TC
|
543 |
3^TW |
596 |
6^TC*_c
|
649 |
5^TM_2_pc
|
|
491 |
2^TC
|
544 |
4^TW
|
597 |
TC*_c
|
650 |
6^TM_2_pc
|
|
492 |
3^TC
|
545 |
5^TW
|
598 |
3^TC^v_c
|
651 |
TM_2_pc
|
|
493 |
4^TC
|
546 |
6^TW
|
599 |
4^TC^v_c
|
652 |
4^TM_2*_pc
|
|
494 |
5^TC
|
547 |
TW
|
600 |
5^TC^v_c
|
653 |
5^TM_2*_pc
|
|
495 |
6^TC
|
548 |
3^TC_p
|
601 |
6^TC^v_c
|
654 |
6^TM_2*_pc
|
|
496 |
TC
|
549 |
4^TC_p
|
602 |
TC^v_c |
655 |
TM_2*_pc
|
|
497 |
1^TC*
|
550 |
5^TC_p
|
603 |
3^TM_1_c
|
656 |
4^TW_pc
|
|
498 |
2^TC*
|
551 |
6^TC_p
|
604 |
4^TM_1_c |
657 |
5^TW_pc
|
|
499 |
3^TC*
|
552 |
TC_p
|
605 |
5^TM_1_c
|
658 |
6^TW_pc
|
|
500 |
4^TC*
|
553 |
3^TC*_p
|
606 |
6^TM_1_c
|
659 |
TW_pc
|
|
501 |
5^TC*
|
554 |
4^TC*_p
|
607 |
TM_1_c
|
660 |
3^TC_ch
|
|
502 |
6^TC*
|
555 |
5^TC*_p
|
608 |
3^TM_1*_c
|
661 |
4^TC_ch
|
|
503 |
TC*
|
556 |
6^TC*_p
|
609 |
4^TM_1*_c
|
662 |
5^TC_ch
|
|
504 |
0^TC^v
|
557 |
TC*_p
|
610 |
5^TM_1*_c
|
663 |
6^TC_ch |
|
505 |
1^TC^v
|
558 |
3^TC^v_p
|
611 |
6^TM_1*_c
|
664 |
TC_ch
|
|
506 |
2^TC^v
|
559 |
4^TC^v_p
|
612 |
TM_1*_c
|
665 |
3^TC*_ch |
|
507 |
3^TC^v
|
560 |
5^TC^v_p
|
613 |
3^TM_2_c
|
666 |
4^TC*_ch
|
|
508 |
4^TC^v
|
561 |
6^TC^v_p
|
614 |
4^TM_2_c
|
667 |
5^TC*_ch
|
|
509 |
5^TC^v
|
562 |
TC^v_p
|
615 |
5^TM_2_c
|
668 |
6^TC*_ch
|
|
510 |
6^TC^v
|
563 |
3^TM_1_p
|
616 |
6^TM_2_c
|
669 |
TC*_ch
|
|
511 |
TC^v
|
564 |
4^TM_1_p
|
617 |
TM_2_c
|
670 |
3^TC^v_ch
|
|
512 |
0^TM_1
|
565 |
5^TM_1_p
|
618 |
3^TM_2*_c
|
671 |
4^TC^v_ch
|
|
513 |
1^TM_1 |
566 |
6^TM_1_p
|
619 |
4^TM_2*_c
|
672 |
5^TC^v_ch
|
|
514 |
2^TM_1
|
567 |
TM_1_p
|
620 |
5^TM_2*_c
|
673 |
6^TC^v_ch
|
|
515 |
3^TM_1 |
568 |
3^TM_1*_p
|
621 |
6^TM_2*_c
|
674 |
TC^v_ch
|
|
516 |
4^TM_1
|
569 |
4^TM_1*_p
|
622 |
TM_2*_c
|
675 |
3^TM_1_ch
|
|
517 |
5^TM_1
|
570 |
5^TM_1*_p
|
623 |
3^TW_c
|
676 |
4^TM_1_ch
|
|
518 |
6^TM_1
|
571 |
6^TM_1*_p
|
624 |
4^TW_c
|
677 |
5^TM_1_ch
|
|
519 |
TM_1
|
572 |
TM_1*_p
|
625 |
5^TW_c
|
678 |
6^TM_1_ch
|
|
520 |
1^TM_1*
|
573 |
3^TM_2_p
|
626 |
6^TW_c
|
679 |
TM_1_ch |
|
521 |
2^TM_1*
|
574 |
4^TM_2_p |
627 |
TW_c
|
680 |
3^TM_1*_ch
|
|
522 |
3^TM_1*
|
575 |
5^TM_2_p
|
628 |
4^TC_pc
|
681 |
4^TM_1*_ch
|
|
523 |
4^TM_1*
|
576 |
6^TM_2_p
|
629 |
5^TC_pc
|
682 |
5^TM_1*_ch
|
|
524 |
5^TM_1*
|
577 |
TM_2_p
|
630 |
6^TC_pc
|
683 |
6^TM_1*_ch
|
|
525 |
6^TM_1*
|
578 |
3^TM_2*_p
|
631 |
TC_pc
|
684 |
TM_1*_ch
|
|
526 |
TM_1*
|
579 |
4^TM_2*_p
|
632 |
4^TC*_pc
|
685 |
3^TM_2_ch
|
|
527 |
1^TM_2
|
580 |
5^TM_2*_p
|
633 |
5^TC*_pc |
686 |
4^TM_2_ch
|
|
528 |
2^TM_2
|
581 |
6^TM_2*_p
|
634 |
6^TC*_pc
|
687 |
5^TM_2_ch
|
|
529 |
3^TM_2
|
582 |
TM_2*_p
|
635 |
TC*_pc
|
688 |
6^TM_2_ch
|
|
530 |
4^TM_2
|
583 |
3^TW_p
|
636 |
4^TC^v_pc
|
689 |
TM_2_ch
|
|
531 |
5^TM_2
|
584 |
4^TW_p
|
637 |
5^TC^v_pc
|
690 |
3^TM_2*_ch
|
|
532 |
6^TM_2
|
585 |
5^TW_p
|
638 |
6^TC^v_pc
|
691 |
4^TM_2*_ch
|
|
533 |
TM_2
|
586 |
6^TW_p
|
639 |
TC^v_pc
|
692 |
5^TM_2*_ch |
|
534 |
1^TM_2*
|
587 |
TW_p
|
640 |
4^TM_1_pc
|
693 |
6^TM_2*_ch
|
|
535 |
2^TM_2*
|
588 |
3^TC_c
|
641 |
5^TM_1_pc
|
694 |
TM_2*_ch
|
|
536 |
3^TM_2*
|
589 |
4^TC_c
|
642 |
6^TM_1_pc
|
695 |
3^TW_ch
|
|
537 |
4^TM_2*
|
590 |
5^TC_c
|
643 |
TM_1_pc
|
696 |
4^TW_ch
|
|
538 |
5^TM_2*
|
591 |
6^TC_c
|
644 |
4^TM_1*_pc
|
697 |
5^TW_ch
|
|
539 |
6^TM_2*
|
592 |
TC_c
|
645 |
5^TM_1*_pc
|
698 |
6^TW_ch
|
|
540 |
TM_2* |
593 |
3^TC*_c
|
646 |
6^TM_1*_pc
|
699 |
TW_ch
|
|
541 |
1^TW |
594 |
4^TC*_c |
647 |
TM_1*pc |
|
|
Notation in text: 
, 
, 
, 
, 
, 
, 
, 
is the overall-index
sign. For the molecule each connected subgraph up to size is constructed. 
is one of these: M_1
for first , M_2 for second , W for Wiener index . C represents the sum over vertex degree of each atom . C^v represents the sum over valence vertex degree of each atom .
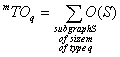
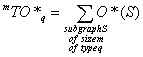
where is the order (this is
also called the “size” or “the number of edges”) of the subgraphs of the H-suppressed
molecular graph; if is specified (as path,
cluster, path-cluster, chain), only subgraphs of this type are used (see 459-488).
The sums run over the subgraphs (regarding and if denoted) and sum up
the values of the indices specified (e.g. W for Wiener index) of the subgraphs.
In 
, 
, 
calculations the values of the vertices
of the subgraphs are used. If no asterisk appears in the symbol of an index,
then these are taken as they are in the parent graph. If an asterisk appears in
the symbol of an index, then the values are taken as
they are in the respective isolated subgraph.
For see 45, for see 46, for see 44, for see vertex degree, for see valence vertex degree.
Source:
· Bonchev,
D.; Trinajstić, N. Overall Molecular Descriptors. 3. Overall
· Bonchev, D. The Overall Wiener Index – A New Tool for Characterization of Molecular Topology. J. Chem. Inf. Comput. Sci. 2001, 41, 582-592
· Bonchev, D. Overall Connectivity – A Next Generation Molecular Connectivity. J. Mol. Graphics Model. 2001, 20, 65-75
· Bonchev,
D. Overall Connectivities/Topological Complexities: A New Powerful Tool for
QSPR/QSAR. J. Chem. Inf. Comput. Sci.
2000, 40, 934-941
R is a descriptor of the category 'topological'.
Notation in text: 
where is the number of atoms
in the H-suppressed molecular graph and is an entry of the
distance matrix.
For see 0 and for see distance matrix.
Source:
TodCon, page 112
con.comp. is a descriptor of the category 'topological'.
Notation in text: 
In most cases, this index is equal to 1. If the compund is made of more than one component, the index increases.
gt planar is a descriptor of the category 'topological'.
Notation in text: 
Source:
· Rücker,
C.; Meringer, M. How Many Organic Compunds are gt-nonplanar? MATCH-Commun. Math. Comput. Chem. 2002, 45, 159-172
D_3D is a descriptor of the category 'geometrical'.
Notation in text: 
is the maximum
distance of two points on the vdw-surface of the molecule incl. H atoms:
For vdw-surface see 374.
V_sphere is a descriptor of the category 'geometrical'.
Notation in text: 
is the volume of the
enclosing sphere (incl. vdw-radii) of the molecule incl. H atoms:
For vdw-radii see 288,
for see 704.
rel. N_rings is a descriptor of the category 'topological'.
Notation in text: 
is the relative number
of rings. It is relative to the number of atoms of an H-suppressed molecule:
where is the number of
rings.
rel. C is a descriptor of the category 'topological'.
Notation in text: 
is the relative
cyclomatic number. It is relative to the number of atoms of an H-suppressed
molecule:
where is the cyclomatic number.
The adjacency matrix (not to be confused
with the descriptor number of atoms ) is defined as:
The modifying term (in e.g. Kier and Hall
shape and flexibility indices, see 65-68) is defined as:
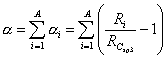
where 
is the covalent radius
of the ith atom in an H-suppressed molecule and 
is the covalent radius
of a sp3 carbon atom:
|
Atom / Hybrid |
|
|
Atom / Hybrid |
|
|
||||||
|
|
Csp3 |
0.77 |
|
0.00 |
|
|
Psp3 |
1.10 |
|
0.43 |
|
|
|
Csp2 |
0.67 |
|
-0.13 |
|
|
Psp2 |
1.00 |
|
0.30 |
|
|
|
Csp |
0.60 |
|
-0.22 |
|
|
Ssp3 |
1.04 |
|
0.35 |
|
|
|
Nsp3 |
0.74 |
|
-0.04 |
|
|
Ssp2 |
0.94 |
|
0.22 |
|
|
|
Nsp2 |
0.62 |
|
-0.20 |
|
|
F |
0.72 |
|
-0.07 |
|
|
|
Nsp |
0.55 |
|
-0.29 |
|
|
Cl |
0.99 |
|
0.29 |
|
|
|
Osp3 |
0.74 |
|
-0.04 |
|
|
Br |
1.14 |
|
0.48 |
|
|
|
Osp2 |
0.62 |
|
-0.20 |
|
|
I |
1.33 |
|
0.73 |
|
Source: TodCon, page 250
is a square matrix of
dimension 
, where is the number of rows
(and columns). is equal to the descriptor
(number of non-H
atoms). Entries are the integers …, -1, 0, 1, 2, … . is calculated by
matrix 
and the vertex degree :
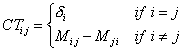
with is defined as:
where is the adjacency
matrix, matrix 
is defined by the
entries in the distance matrix :
For see vertex degree, for see adjaceny matrix, for and see distance matrix.
is a square matrix of
dimension , where is the descriptor (number of non-H atoms).
Entries are 0, 1, 2, …
An entry 
represents the length
of the longest path from atom (vertex) to atom (vertex) in a molecular graph
without H atoms. Many authors set 
for all vertices :
There is also a detour matrix 
which includes closed detours
(rings of maximal length) from atom i to itself:
For see 0.
Source:
Buckley, F.; Harary F. Distance in Graphs. Addison-Wesley,
Ivanciuc, O.; Balaban, A. T. Design of Topological Indices. Part 8. Path Matrices and Derived Molecular Graph Invariants. MATCH - Commun. Math. Comp. Chem. 1994, 30, 141-152
Rücker, G.; Rücker, C.
Symmetry-Aided Computation of the Detour Matrix and the Detour Index. J. Chem. Inf. Comput. Sci. 1998, 38, 710-714
TodCon, page 103
is a square matrix of
dimension , where is the descriptor (number of non-H
atoms). Entries are 0, 1, 2, …
An entry represents the length
of the shortest path from atom (vertex) to atom (vertex) in an H-supressed
molecular graph.
is also called the
distance of atom to atom .
For see 0.
is the maximum entry
in the ith line of the distance matrix of an H-suppressed graph:
is the distance of
atom i to atom j. is the number of
atoms.
For see 0. For see distance matrix.
Source:
· TodCon, page 112
(or ) in e.g. Ren’s AI indices (see 377-456) is the modified vertex
degree of the atom in an H-suppressed
molecule. It is defined as the number of neighbours of atom (=) modified by the value 
.
where is defined as:
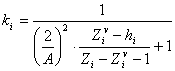
where is the number of
atoms, 
is the number of H
atoms attached to atom , 
is the number of valence
electrons of atom and 
is the atomic number
of atom .
See also valence vertex degree.
For see vertex degree, for see 0.
is a square matrix of
dimension , where is equal to the
descriptor (number of non-H
atoms). Entries are 0, 1, 2, …
A entry 
is the number of atoms
being closer to than to :
Source:
· TodCon, page 438
The unsaturated adjacency matrix is defined as:
is defined as the ith
row sum of the unsaturated distance matrix 
of an H-suppressed
molecular graph:
For see 0. For and 
see unsaturated distance matrix.
is a square matrix of
dimension , where is equal to the
descriptor (number of non-H
atoms).
An entry represents the length
of the shortest path from atom (vertex) i to atom (vertex) j in a H-supressed
molecular graph. Single bonds represent a distance of 1, double bonds represent
a distance of 
, triple bonds represent a distance of 
, aromatic bonds represent a distance of 
:
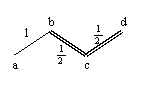
In this example, the distance 
from 
to is 
and the distance 
is 
.
For see 0.
is the valence vertex
degree of atom in an H-suppressed
molecule:
with 
is the number of
valence electrons of atom , is the number of H
atoms attached to atom , and is the total number of
electrons (= the atomic number) of atom .
is the vertex degree
of atom in an H-suppressed
molecule. It is defined as the number of neighbours of atom , which is the ith row sum of the adjacency matrix
where is equal to the
descriptor (number of non-H
atoms).
is defined as the ith
row sum of the distance matrix of an H-suppressed
molecular graph:
For see 0. For and see distance matrix.
| © OLGEN |
exit | by Joachim Braun and Christoph Rücker |
