


Next: The computation of
Up: MOLGEN, a generator of...
Previous: Introduction
As already said, MOLGEN has as input
- the chemical formula, (optionally)
prescribed and forbidden substructures,
an interval for the allowed ring sizes, and
maximal bond multiplicities.
The input of the chemical formula is done as usual, you simply enter names of
atoms, like 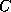 for carbon, and the multiplicity of the atoms you want to have in
the molecule in question. Of course, as these names are arbitrary, you may also
use phantasy names for them. As soon as you entered the number,
you either accept the default value for the valence of that atom (4 in case
of carbon etc.), or you may choose another value for the valence. Hence
you can enter, say, sulphur atoms by the names
for carbon, and the multiplicity of the atoms you want to have in
the molecule in question. Of course, as these names are arbitrary, you may also
use phantasy names for them. As soon as you entered the number,
you either accept the default value for the valence of that atom (4 in case
of carbon etc.), or you may choose another value for the valence. Hence
you can enter, say, sulphur atoms by the names 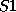 and
and 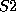 and prescribe
different valences for them if required.
and prescribe
different valences for them if required.
Once you have entered the chemical formula, it is checked if
molecular graphs with this sequence of numbers and valences of atoms can exist. If
this is not the case you will get a corresponding error message.
The next step is the input of prescribed and of forbidden substructures.
We would like in particular to outline that there are three types
of substructures that can be entered optionally, namely:
- The most important substructures are macroatoms,
which mean substructures that are not allowed to overlap. These macroatoms
are very important, since they may reduce the work of the generator
tremendously.
- The second type are substructures which form the so-called goodlist; they may overlap. This list is applied as a
filter after the generation process.
- The forbidden substructures form the so-called badlist. This list
is used in the analogous way as a filter following the generation.
Using this input, MOLGEN generates the following output:
- The complete list of all the mathematically possible molecular graphs that
are compatible with the chemical formula (i.e. the vertices are labelled with
the element names, they have the prescribed valences, and the graph is
connected).
In contrast to the well-known historical forerunner
DENDRAL (cf. [3]) and to previous
versions of MOLGRAPH (as it was called at the
beginning) and MOLGEN (see [4]), the current version
does not depend on a catalogue of precomputed
cyclic molecular graphs, which
limited the range of the generator. The limit of this generator
is only given by the speed of the machine as far as
the generation is concerned. If the molecular graphs shall
be saved, it is, of course, also the space on the hard disk that matters.
The mathematical concept behind MOLGEN is a mixture of combinatorial and
algebraic methods. In particular orderly generation is intensively used,
details are given in [5]. Its application in molecular structure
elucidation stands or falls with the input. The main emphasis should lie on
the macroatoms, since a big set of prescribed and nonoverlapping substructures
reduces the problem of generation considerably, while the goodlist and the
badlist can be
applied only after the generation.
The macroatoms in fact shrink to a point
in the eyes of the generator. For example, if you use the skeleton of the
dioxin molecule (see fig. 1), say, as a macro-atom,
it shows up as a single point in the generated graphs, which is a single
graph in this particular example, and so, here the generator needs to
construct one graph only, instead of 22. Of course, the full set of isomers
is obtained afterwards by the so-called
expansion of the macroatoms, including an isomorphism check. But this
separation of generation and expansions splits the total problem into two
pieces, which increases the reach considerably.
The aim of structure elucidation
is to obtain the complete set of molecular graphs that correspond to given
data, and this set of candidates should be as small as possible, which
means that we have to interpret the data carefully to get - first of
all - the biggest possible set of macroatoms. An example is given below.
Table 1 gives an impression of what happens if only the chemical
formula is entered. The reader immediately sees how complex the problem is
and that he should try to find further conditions very intensively.
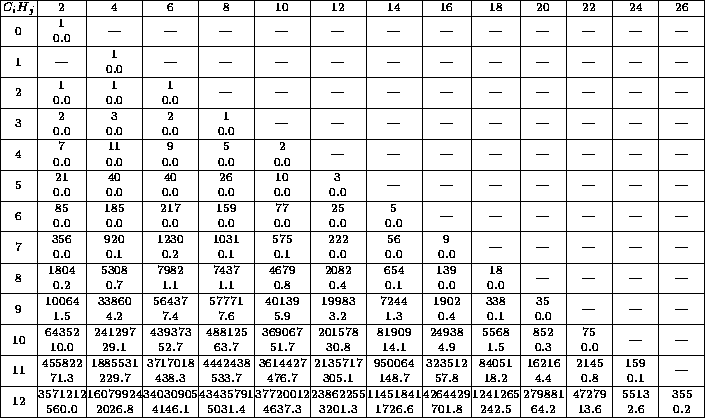
Table 1: Each table entry contains the number of isomers and
the CPU-time in seconds.
The row index 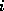 denotes the number of C-atoms, the column index
denotes the number of C-atoms, the column index
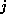 the number of H-atoms. The times were computed on a HP-9000/705,
which is approximately as fast as a 486DX2/66 PC running OS/2.
the number of H-atoms. The times were computed on a HP-9000/705,
which is approximately as fast as a 486DX2/66 PC running OS/2.
The table 1 shows that it is very important to impose as many
restrictions as possible in order to make the generator construct as few
as possible molecular graphs. Therefore, besides the restrictions by
giving prescribed and forbidden substructures, you can also enter
conditions on the size of rings, where you may in fact enter an interval, say
from 4 to 6 in order to exclude, say, 3-rings in a molecule with the
gross formula 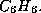 Moreover, you may also restrict the multiplicity of
bonds.
Moreover, you may also restrict the multiplicity of
bonds.



Next: The computation of
Up: MOLGEN, a generator of...
Previous: Introduction
Send questions to: molgen@btm2x2.mat.uni-bayreuth.de

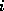 denotes the number of C-atoms, the column index
denotes the number of C-atoms, the column index
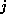 the number of H-atoms. The times were computed on a HP-9000/705,
which is approximately as fast as a 486DX2/66 PC running OS/2.
the number of H-atoms. The times were computed on a HP-9000/705,
which is approximately as fast as a 486DX2/66 PC running OS/2.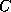 for carbon, and the multiplicity of the atoms you want to have in
the molecule in question. Of course, as these names are arbitrary, you may also
use phantasy names for them. As soon as you entered the number,
you either accept the default value for the valence of that atom (4 in case
of carbon etc.), or you may choose another value for the valence. Hence
you can enter, say, sulphur atoms by the names
for carbon, and the multiplicity of the atoms you want to have in
the molecule in question. Of course, as these names are arbitrary, you may also
use phantasy names for them. As soon as you entered the number,
you either accept the default value for the valence of that atom (4 in case
of carbon etc.), or you may choose another value for the valence. Hence
you can enter, say, sulphur atoms by the names 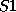 and
and 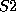 and prescribe
different valences for them if required.
and prescribe
different valences for them if required.
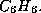 Moreover, you may also restrict the multiplicity of
bonds.
Moreover, you may also restrict the multiplicity of
bonds.