| Induced cycle indices |
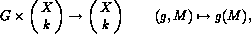 where g(M):={gm | mÎM} .
where g(M):={gm | mÎM} .
In the special case of k=2, X={1,...,n} , n³2 and G=Sn this situation describes the group action of Sn on the set of all linear graphs with n vertices.
By the same definition the group G acts on the power set of X (i.e. the set of all subsets of X). The following routines allow to calculate these induced cycle indices:
INT zykelind_on_2sets(a,b) OP a,b; INT zykelind_on_ksubsets(a,c,b) OP a,b,c; INT zykelind_on_power_set(a,b) OP a,b;In all these cases
a is the cycle index of the group action GX.
The induced cycle index will be computed as b.
In order to define the
cardinality of k-subsets of X, c is an INTEGER
object which is the
value of k.
The group action GX induces a group action on the set Xk, the set of all k-tuples of X, and on Xk, the set of all injective k-tuples of X for k<|X|. These group actions are defined by
G´Xk -> Xk (g,v) -> gv,
G´Xk -> Xk (g,v) -> gv,where gv=g(v1,...,vk):=(gv1,...,gvk).
In the special case of k=2, X={1,...,n} , G=Sn the situation of injective 2-tuples describes the group action of Sn on the set of all directed graphs with n vertices without loops. The situation of general 2-tuples describes the group action of Sn on the set of all directed graphs with n vertices and loops permitted. The following routines allow to calculate these induced cycle indices:
INT zykelind_on_pairs(a,b) OP a,b; INT zykelind_on_pairs_reduced(a,b) OP a,b; INT zykelind_on_ktuples(a,c,b) OP a,b,c; INT zykelind_on_ktuples_injective(a,c,b) OP a,b,c;In all these cases
a is the cycle index of the group action GX. The
induced cycle index will be computed as b. In order to define the
parameter k the INTEGER object c is used.
All these induced cycle indices can be computed by defining linear operators which act on a given cycle index. See for instance [1]. In this book some other situations are investigated as well. For instance in order to distinguish between edges (i, j), for i different from j and loops (i, i) in a directed graph, two families of indeterminates should be used. The first family takes the information about cycle lengths of edges, the second takes the information about loops. In order to enumerate the number of classes of directed graphs with loops a 2-dimensional form of Pólyas Theorem is used. This procedure can be done with
INT zykelind_on_pairs_disjunkt(a,b) OP a,b;The cycle index of the group action on the set of vertices is
a. The
induced cycle index is b. This is a
2-dimensional form of a cycle index.
In [1] the authors are dealing with superpositions of a linear and a directed graph. The corresponding routine in SYMMETRICA is
INT zykelind_superp_lin_dir_graphs(a,b) OP a,b,c;Again this is an application of the 2-dimensional form of a cycle index.
a is the number of vertices of the graphs (an INTEGER object).
The computed cycle index is b.
Another example for the enumeration of graphs are the so called oriented graphs. An oriented graph is a directed graph, such that whenever an edge (i, j) occurs in the graph, the edge (j,i) must not occur in it. The cycle index of the induced group action can be computed by
INT zykelind_on_pairs_oriented(a,b) OP a,b;
a is the cycle index of the group action on the "points", b
is the induced cycle index.
Tournaments of n players can be interpreted as oriented graphs with maximal
number of edges. In order to enumerate the number of "different" tournaments
of n players each indeterminate xi in the cycle index a must be
replaced by 1+2zi, where z is an indeterminate. This can be done by
using the routine
polya1_sub.
| Induced cycle indices |