| Species |
Consider the category F of finite sets with bijections. It consists of the two classes Obj(F) of objects M,N,..., the finite sets, and the class Mor(F) of morphisms f,g,..., which are the bijections between finite sets. Mor(M,N) denotes the set of morphisms between the sets M and N:
Mor(M,N):={f:M -> N | f is a bijection}.(Note that the categorical definition of mappings identifies f:M -> N with the triple (M,{(m,f(m)) | mÎM},N), and hence, if (M,N) not = (M',N'), then Mor(M,N)ÇMor(M',N')=Æ.) Moreover the definition of category assumes a multiplication
o :Mor(L,M)´Mor(M,N) -> Mor(L,N):(f,g) -> g o f,which is associative. In our case this is of course the usual composition of mappings. Furthermore the definition of category requires a neutral element 1MÎMor(M,M) (neutral with respect to the multiplication mentioned above), it is the identity mapping here.
A species A is a (covariant) functor on F. This means the following: A consists of a mapping from Obj(F) to Obj(F), which we also denote by A, for sake of simplicity of notation, together with a mapping from Mor(F) to Mor(F) which will be denoted by A, too:
A:Obj(F) -> Obj(F):M -> A(M),and
A:Mor(F) -> Mor(F):f -> A(f),where A(f)ÎMor(A(M),A(N)), and such that
A(g o f)=A(g) o A(f), and A(1M)=1A(M).The set A(M) is called the set of labelled A-structures on M, A(f) is called the transport of A-structures along f. The elements of M are called points, and the elements aÎA(M) are called elements of A, which is abbreviated by aÎA. Let us consider a bunch of examples before we go into details.
Examples:
- The species labelled graphs G is defined by
G(M):={g | g labelled graph with vertex set M},and G(f) maps gÎG(M) ontog':=G(f)(g),where g' arises from g by simply replacing the label mÎM by the label f(m)ÎN, for each bijection f between M and N.- The species permutations S is defined by mapping M onto the symmetric group SM on M:
S(M):=SM={p:M -> M | p is bijective},and S(f) is defined to be renumbering according to f, which means that, for each pÎSM, we haveS(f)(p):=f o p o f-1ÎSN, for fÎMor(M,N).- The species linear orders L maps M onto the set of all the | M | ! linear orders on M:
L(M):={(mi1<...<mi | M | ) | min ÎM, min not = mim,n not =m}.The morphism L(f) means simply replacing m by f(m):L(f)(mi1<...<mi | M | ):=(f(mi1)<...<f(mi | M | )).- The species set E is defined by
E(M):={M}, E(f)(M):=f(M).- The empty species Æ maps each M onto the empty set and therefore Æ(f) must always be the empty mapping.
- The species empty set 1 maps the set Æ onto {Æ}, and all the other M onto Æ, so that each morphism f not =Æ is mapped onto the empty mapping Æ, while the empty mapping, being an element of Mor(Æ,Æ), is mapped onto the identity mapping on {Æ}.
- The species singleton X is defined by
X(M):={m} if M={m}X(M):=Æ otherwiseandX(f):=1M if M={m}X(f):=Æ otherwise- The species endofunctions F maps M onto MM, while, for each f in Mor(M,N) we put
F(f)(j):=f o j o f-1ÎNN, for each jÎMM.- The species F0, the endofunctions with fixed point, maps M onto
F0(M):={jÎMM | $mÎM:j(m)=m},while F0(f)(j)=f o j o f-1, as before.- The species idempotent endofunctions K maps M onto the following subset of F(M):
K(M):={jÎMM | j2=j},and again it has K(f):=f o j o f-1.
Let us return to the consideration of a general species A again. We recall that it maps a morphism f:M -> N onto A(f), which is a bijection from A(M) onto A(N). We may therefore call A(f) a relabeling of the a in A(M), so that the A-structures on N arise from the A-structures on M by relabeling. Thus it suffices (up to relabeling) to define A on each of the sets n, where nÎN.
Examples: The species labelled trees T maps n onto the setUsing this fact that it suffices, up to relabeling, to describe A(n), we introduce, for each species A, the corresponding generating function called the cardinality of A:T(n):={g | g tree with vertex set n},and g'=T(f)(g) is the tree obtained from g by replacing the label iÎn by f(i)ÎN, if fÎMor(n,N). Correspondingly the species labelled rooted trees T0 is defined byT0(n):={t:=(g,i) | gÎT(n),iÎn},the element i of (g,i) is called the root of t.
A(x):=ånÎN | A(n) | (xn)/(n!).
Examples: For the cardinalities of the preceding examples we have:Correspondingly two species A and B are called equipotent, if and only if A(x)=B(x). We abbreviate this by writingG(x)=ån2[n choose 2](xn)/(n!), S(x)=L(x)=(1)/(1-x), E(x)=ex,Æ(x)=0, 1(x)=1, X(x)=x, F(x)=ånnn(xn)/(n!).
A~B.A stronger condition is isomorphy, for short:
A simeq B,in which we require canonic bijections QM:A(M) -> B(M) which satisfy
B(f) o QM=QN o A(f), for each fÎMor(M,N).It is clear that the following holds:
A simeq BÞA~B.The converse is not true, as it is shown by
Example: Clearly the species S of permutations and the species L of linear orders are equipotent. Let us assume that there exist bijections Qn:S(n) -> L(n), which satisfyWe shall now use set theoretic operations in order to introduce on the isomorphism classes of species a semiring structure. The operation of addition is defined by disjoint union as follows:L(f) o Qn=Qn o S(f),for each bijection f:n -> n. Consider an n>1, a bijection f which is not the identity mapping, and apply both sides of the identity to p:=1ÎSn =S(n). The left hand side yields, ifQn(p)=:(i1<...<in)ÎL(n),that(L(f) o Qn)(p)=L(f)(i1<...<in)=(f(i1)<...<f(in)),while an application of the right hand side gives(Qn o S(f))(p)=Qn(f o p o f-1)=Qn (1)=(i1<...<in) not =(f(i1)<...<f(in)).
(A+B)(n):=A(n) DOTCUP B(n).The species A+B, called the species sum of A and B, or simply the sum of A and B, has as its set of transport on n the disjoint union of the set of mappings A(f) and B(f), where f in both cases runs through the bijective f:n -> n. The multiplication uses the cartesian product:
(A·B)(n):=ÈM DOTCUP N=nA(M)´B(N)=ÈMÍnA(M)´B(n\M).Since a set R together with operations + and · is called a semiring if and only if both (R,+) and (R,·) are commutative semigroups, 0 is neutral with respect to +, 1 is neutral with respect to ·, 0r=0, for each rÎR, and the distributivity law (r+s)t=rt+rs holds, we obtain
Lemma: The isomorphism classes of species form a semiring with respect to addition and multiplication. The neutral element with respect to addition is the empty species Æ while the neutral element with respect to multiplication is the species empty set 1.The necessary checks are straightforward. But there are several other important operations on species. Before we start defining these let us introduce a helpful notation which allows us to illustrate the various situations. In order to sketch an A-structure aÎA(4), say, we write

the a and the box maybe left out, so that an element of (A+B)(4) is of the following form:
while an element of (A·B)(5) looks as follows:
for example, an element of (S·G)(7) is such a pair (pg), where p is a permutation, say (135)ÎSM, M:={1,3,5}, and g is a labelled graph on N={2,4,6,7}, with edge set {{2,3},{3,5}}. We use this notation also in order to illustrate the plethysm B
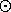 A, defined
as follows:
A, defined
as follows:
(Bwhere the disjoint union is taken over all the set partitions p of n. For example, an element of BA)(n):=Èp={p1,...,pm} Õi=1mB(pi)´A(m),
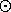 A(6), arising from
the partition p:={{1,4,5},{2,6},{3}} looks as follows:
A(6), arising from
the partition p:={{1,4,5},{2,6},{3}} looks as follows:
The plethysm of structures has many interesting properties, for example the singleton X is neutral with respect to plethysm:
A simeq XProof: We obtain from the definition of plethysm thatA simeq A
X.
(Xbut X(pi) is empty except when | pi | =1, so that this union is in fact taken over the single partition p={{1},..., {n}} of n, and thereforeA)(n)=ÈpÕi=1mX(pi)´A(m),
(XIt is quite often helpful to recognize species as plethysms of species. For example, if C denotes the species of cyclic permutations, i.e.A)(n)=A(n).
C(n):={sÎS(n) | " 0<j<n:sj1 not =1},then obviously
S simeq Csince each permutation is a union of its disjoint cyclic factors. This motivates us to say that, in case A simeq BE,
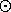 E, B is the species
of connected
A-structures.
An example is the decomposition of labelled graphs into their
connected components:
E, B is the species
of connected
A-structures.
An example is the decomposition of labelled graphs into their
connected components:
G simeq Zwhere Z denotes the species connected graphs .E,
Another interesting notion is that of the derivative. It associates with A the species A', which is obtained by adding to the set n a further and anonymous element, we indicate it by *, and then applying A:
A'(n):=A(n+), where n+:=nÈ{*}.A further helpful concept is that of punctuation, where A is mapped onto
A·(n):=A(n)´n.The corresponding generating functions clearly satisfy
A'(x)=(d)/(dx)A(x), A·(x)=x·(d)/(dx)A(x).So far each element aÎA is a labelled structure, for example a labelled graph. In order to get rid of the labeling we have of course to introduce the canonical action
Sn ´A(n) -> A(n):(s,a) -> A(s)a.An orbit is called a type of A-structure. Furthermore we denote by Tn(A) a transversal of Sn \\A(n), so that we obtain a transversal
T(A):=ÈnÎNTn(A)of all the types of A-structures. The set
[~A] (n):={(s,a) | aÎA(n),sÎSn :A(s)a=a}is called the species associated with A. Its generating function [~A] is
[~A] (x):=ånÎN | Tn(A) | xn.And hence the ordinary generating function for the A-types is the exponential generating function for the species [~A] .
Now we would like to apply to species what we know about cycle indicator polynomials. For this purpose we introduce the following formal power series:
ZA:=ZA(x1,x2,...):=åaÎT(A)C((Sn )a,n; x1,x2,...),where (Sn )a denotes the stabilizer of aÎA(n) in Sn . Hence, for example (exercise):
ZX=x1, ZE=exp(åi(xi)/(i)), ZL=(1)/(1-x1), ZS= Õi(1)/(1-xi) .Since
C((Sn )a,n;x1,0,...)=(1)/( | (Sn )a | )x1n,and
C((Sn )a,n;x,x2,x3,...)=xn,we obtain
ZA(x,0,...)=A(x), and ZA(x,x2,x3,...)=[~A] (x).Exercises
E: Provethe correctness of the cycle index series above..
| Species |