The functional equation of the mean sun written as a
group action
HARALD FRIPERTINGER*
Local solar time is measured by a sundial. When the center of the sun is on an observer’s
meridian, the observer’s local solar time is zero hours (noon). Because the earth moves with
varying speed in its orbit at different times of the year and because the plane of the earth’s
equator is inclined to its orbital plane, the length of the solar day is different depending on the
time of year. It is more convenient to define time in terms of the average of local solar time.
Such time, called mean solar time, may be thought of as being measured relative to an
imaginary sun (the mean sun) that lies in the earth’s equatorial plane and about
which the earth orbits with constant speed. Every mean solar day is of the same
length.1
In [5, 2] it is shown that the mean sun satisfies the functional equation
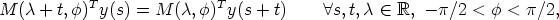
where y(s) is a vector of length 1 which is the direction from the center of the
earth to the sun at the time s (one day corresponds to 2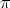 ) expressed in a geocentric
coordinate system. As a basis of this system we can choose two orthogonal vectors
in the equatorial plane and one vector along the axis of the earth. M(
) expressed in a geocentric
coordinate system. As a basis of this system we can choose two orthogonal vectors
in the equatorial plane and one vector along the axis of the earth. M(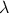 ,
, 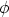 ) is the
matrix
) is the
matrix
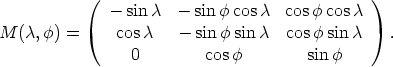
Then M(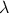 ,
, 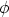 )y(s) is the direction from the earth to the sun expressed in a local coordinate
system on the surface of the earth in the point of longitude
)y(s) is the direction from the earth to the sun expressed in a local coordinate
system on the surface of the earth in the point of longitude 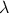 and latitude
and latitude 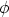 . This local
coordinate frame is given by the unit vectors indicating the directions East, North, and to the
zenith.
. This local
coordinate frame is given by the unit vectors indicating the directions East, North, and to the
zenith.
In the present paper we investigate a generalization of this equation for fixed 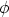 . To be
more precise, we will deal with the following problem:
. To be
more precise, we will deal with the following problem:
Let (G, .) be a group acting on a set X (cf. [1, 3, 4, 6]) and let (R, +) be a not necessarily
commutative group. Find all functions x : R  X and g : R
X and g : R  G, which satisfy
G, which satisfy
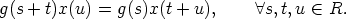 | (1) |
The group R is a generalization of 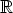 , the matrices expressing the change of the coordinate
system are now elements of the group G, and X represents a generalization of the set of all
vectors in
, the matrices expressing the change of the coordinate
system are now elements of the group G, and X represents a generalization of the set of all
vectors in  3.
First we want to give some basic definitions about group actions. A group action of the
(multiplicative) group G on the set X is given by a mapping
3.
First we want to give some basic definitions about group actions. A group action of the
(multiplicative) group G on the set X is given by a mapping

which satisfies 1x = x and ( 2
2 1)x =
1)x =  2(
2( 1x) for all x
1x) for all x  X and
X and  1,
1,  2
2  G, where 1 is the
identity element in G. In other words, a group action describes a homomorphism from G to
the set of all bijections on X, which is a group together with the composition of functions as
the multiplication in the group. Conversely, each homomorphism of this kind determines a
group action of G on X.
G, where 1 is the
identity element in G. In other words, a group action describes a homomorphism from G to
the set of all bijections on X, which is a group together with the composition of functions as
the multiplication in the group. Conversely, each homomorphism of this kind determines a
group action of G on X.
A group action of G on X defines an equivalence relation on X. Two elements x1, x2 of
x are called G-equivalent, x1 ~ Gx2, if and only if there is some 
 G such that
x2 =
G such that
x2 =  x1. The equivalence classes G(x) with respect to ~ G are called orbits of G on X,
i.e.
x1. The equivalence classes G(x) with respect to ~ G are called orbits of G on X,
i.e.
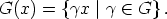
For each x  X the stabilizer Gx of x, which is the set
X the stabilizer Gx of x, which is the set
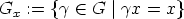
is a subgroup of G.
Two elements x and y of the same orbit have conjugate stabilizers. To be more precise, if
y =  x for
x for 
 G, then Gy =
G, then Gy =  Gx
Gx -1.
-1.
Coming back to the functional equation (1), we start with collecting some properties of the
functions g and x. Later we determine all solutions g and x of (1). In a first step we replace g
by another function h : R  G, defined by
G, defined by
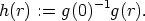
The properties of h are described in
-
- Proof. The first statement is clear from the definition of h. Then h(s)x(u) =
g(0)-1g(s)x(u) = g(0)-1g(0 + s)x(u) = g(0)-1g(0)x(s + u) = x(s + u) for all s, u
 R.
Finally h(s + t)x(u) = g(0)-1g(s + t)x(u) = g(0)-1g(s)x(t + u) = h(s)h(t)x(u) for all
s, t, u
R.
Finally h(s + t)x(u) = g(0)-1g(s + t)x(u) = g(0)-1g(s)x(t + u) = h(s)h(t)x(u) for all
s, t, u  R.
R. ![[]](lasy10-c-32.gif)
It is also possible to determine g by h.
-
- Proof. g(s + t)x(u) = g0h(s + t)x(u) = g0x(s + t + u) = g0h(s)x(t + u) = g(s)x(t + u).
![[]](lasy10-c-32.gif)
For the rest of the paper we will work with h instead of g. As was indicated earlier, for
x  X let Gx denote the stabilizer of x. From (3) we deduce that
X let Gx denote the stabilizer of x. From (3) we deduce that 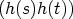 -1h(s + t)
-1h(s + t)  G
x(u)
for all u
G
x(u)
for all u  R and all s, t
R and all s, t  R. In other words
R. In other words
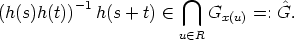
Using this for t = -s, we see that there exists  s
s 
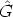 , such that h(s)-1 = h(-s)
, such that h(s)-1 = h(-s) s. And for
s = -t there is
s. And for
s = -t there is  t'
t' 
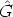 , such that h(t)-1 =
, such that h(t)-1 =  t'h(-t).
t'h(-t).
Let H := <h(R)> and 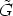 :=
:= 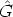
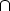 H, then the following lemma holds.
H, then the following lemma holds.
Lemma 3. The subgroup 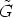 of H is normal.
of H is normal.
-
- Proof. It is clear that
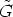 is a subgroup of H. We only have to prove that it is a normal
subgroup. From the definition of H we know that
is a subgroup of H. We only have to prove that it is a normal
subgroup. From the definition of H we know that
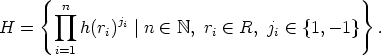
So it is enough to prove that h(r)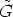 h(r)-1 <
h(r)-1 < 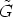 and h(r)-1
and h(r)-1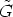 h(r) <
h(r) < 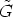 for all r
for all r  R.
Let r, u
R.
Let r, u  R and
R and 

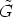 , then there is a
, then there is a  r'
r' 
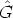 , such that h(r)
, such that h(r) h(r)-1x(u) =
h(r)
h(r)-1x(u) =
h(r)
 r'h(-r)x(u) = h(r)
r'h(-r)x(u) = h(r)
 r'x(-r + u) = h(r)x(-r + u) = x(r - r + u) = x(u), since
r'x(-r + u) = h(r)x(-r + u) = x(r - r + u) = x(u), since

 r'
r' 
 stabilizes each element of the form x(t). This means, since
stabilizes each element of the form x(t). This means, since  was an arbitrary
element of
was an arbitrary
element of 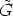 , that
, that
so h(r) h(r)-1 <
h(r)-1 < 
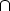 H =
H = 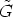 . For the second part of the proof similar arguments can
be used.
. For the second part of the proof similar arguments can
be used. ![[]](lasy10-c-32.gif)
This permits to define a function 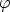 from R to the factor group H/
from R to the factor group H/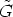 by
by
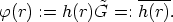
Lemma 4. The mapping 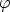 is a surjective group homomorphism.
is a surjective group homomorphism.
-
- Proof. For s, t
 R we know from (3) that h(s)h(t)
R we know from (3) that h(s)h(t)  h(s + t)
h(s + t)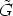 . So
. So
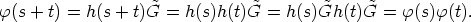
In order to prove that 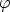 is surjective let
is surjective let
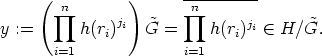
Then
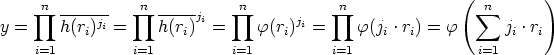
and  i = 1nji . ri
i = 1nji . ri  R.
R. ![[]](lasy10-c-32.gif)
Even the following result is true.
Lemma 5. If a subgroup N of Gx(0) is a normal subgroup of H, then N is a subgroup of
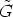 .
.
-
- Proof. It is enough to prove that N is a subgroup of Gx(u) for all u
 R, because then
N is a subgroup of
R, because then
N is a subgroup of 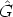 . By assumption N < H, so N <
. By assumption N < H, so N < 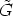 . From (2) it is clear that
x(u) = h(u)x(0) for all u
. From (2) it is clear that
x(u) = h(u)x(0) for all u  R, so Gx(u) = Gh(u)x(0) = h(u)Gx(0)h(u)-1. Since N is a
normal subgroup of H, it is obvious that N = h(u)Nh(u)-1 < h(u)G
x(0)h(u)-1 = G
x(u).
R, so Gx(u) = Gh(u)x(0) = h(u)Gx(0)h(u)-1. Since N is a
normal subgroup of H, it is obvious that N = h(u)Nh(u)-1 < h(u)G
x(0)h(u)-1 = G
x(u).
![[]](lasy10-c-32.gif)
So far we derived necessary conditions for solutions of (2). Before describing sufficient
conditions we prove a general result about group actions.
Lemma 6. Consider a group G acting on a set X. Let S be a subgroup of G, x0 an arbitrary
element of X, and N a normal subgroup of S, such that N is a subgroup of the
stabilizer Gx0. Then the factor group S/N acts on the orbit S(x0) in the following way:
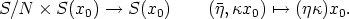 | (4) |
-
- Proof. In order to prove that this action is well defined, consider an arbitrary

 N.
Since N is a normal subgroup of S, for each
N.
Since N is a normal subgroup of S, for each 
 S there exists
S there exists  '
'  N, such that
N, such that

 =
= 
 '. From
'. From
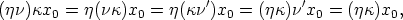
we derive that the action of 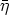 on H(x0) does not depend on the special choice
of the representative of
on H(x0) does not depend on the special choice
of the representative of 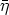 . Furthermore, it is clear that
. Furthermore, it is clear that 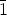
 x0 = 1
x0 = 1 x0 =
x0 =  x0, and
(
x0, and
(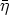 1
1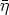 2)
2) x0 =
x0 = 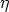 1
1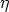 2
2 x0 = (
x0 = (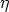 1
1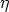 2)
2) x0 =
x0 = 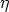 1(
1(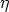 2
2 )x0 =
)x0 = 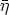 1(
1(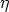 2
2 x0) =
x0) = 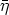 1(
1(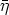 2
2 x0) for all
x0) for all
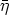 1,
1, 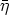 2
2  S/N.
S/N. ![[]](lasy10-c-32.gif)
Under the assumptions of the last lemma, N is a subgroup of each stabilizer G x0 for
x0 for 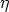
 S,
since
S,
since
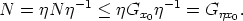
-
- Proof. h(s)x(u) =
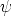 (s)
(s)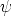 (u)x0 =
(u)x0 = 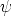 (s + u)x0 = x(s + u) for all s, u
(s + u)x0 = x(s + u) for all s, u  R.
R. ![[]](lasy10-c-32.gif)
Finally all these results are summarized in
-
- Proof. If x and h satisfy (2), then choose x0 = x(0). Moreover, S = H, N =
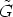 ,
and
,
and 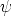 =
= 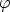 satisfy the above conditions by construction, Lemma 3 and Lemma 4.
Finally, by construction it is clear that h(r)
satisfy the above conditions by construction, Lemma 3 and Lemma 4.
Finally, by construction it is clear that h(r) 
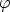 (r), and from (2) it follows that
(r), and from (2) it follows that
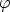 (r)x0 =
(r)x0 = 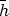 (r)x(0) = x(r) for all r
(r)x(0) = x(r) for all r  R.
R.
The rest of the present theorem follows immediately from Lemma 7. ![[]](lasy10-c-32.gif)
Acknowledgement: The author wants to express his thanks to Professor Jens Schwaiger
for useful comments and hints while preparing this article.
References
[1] P.M. Cohn. Algebra, volume 3. J. Wiley & Sons, Chichester etc., 2nd edition, 1989.
ISBN 0-471-10169-9.
[2] H. Fripertinger and J. Schwaiger. Some applications of functional equations in
astronomy. Grazer Mathematische Berichte, 344 (2001), 1-6.
[3] S. Lang. Algebra. Addison Wesley, Reading, Massachusetts, 3rd edition, 1993. ISBN
0-201-55540-9.
[4] K. Meyberg. Algebra. Teil 1. Carl Hanser Verlag, München, Wien, 2nd edition, 1980.
ISBN 3-446-11965-5.
[5] J. Schwaiger. Some applications of functional equations in astronomy. Aequationes
Mathematicae, 60 (2000), p. 185. In Report of the meeting: The Thirty-seventh
International Symposium on Functional Equations, May 16-23, 1999, Huntington,
WV.
[6] M. Suzuki. Group Theory I. Grundlehren der mathematischen Wissenschaften 247.
Springer Verlag, Berlin, Heidelberg, New York, 1982. ISBN 3-540-10915-3.
HARALD FRIPERTINGER
Institut für Mathematik
Karl-Franzens-Universität Graz
Heinrichstr. 36/4
A-8010 Graz
Austria
harald.fripertinger@kfunigraz.ac.at
|
 s, t, u
s, t, u  R) of the functional equation
of the mean sun is studied, where a group G acts on a set X, (R, +) is a not
necessarily commutative group and both x : R
R) of the functional equation
of the mean sun is studied, where a group G acts on a set X, (R, +) is a not
necessarily commutative group and both x : R  X and g : R
X and g : R  G are unknown
functions, which will be determined by the equation.
G are unknown
functions, which will be determined by the equation.
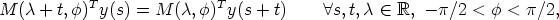
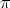
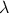 ,
, 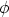
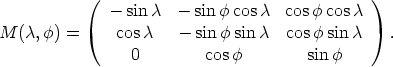

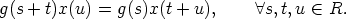
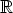



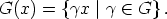
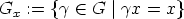
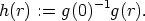
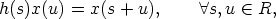
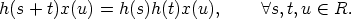
![[]](lasy10-c-32.gif)
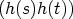
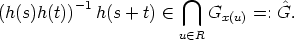
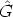 , such that
, such that 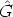 , such that
, such that 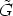 :=
:= 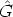
 is a subgroup of
is a subgroup of 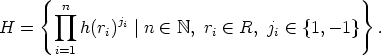
 and
and 
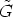 for all
for all 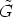 , then there is a
, then there is a 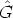 , such that
, such that  stabilizes each element of the form
stabilizes each element of the form 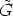 , that
, that
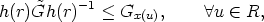
 . For the second part of the proof similar arguments can
be used.
. For the second part of the proof similar arguments can
be used. 
 by
by
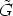 . So
. So
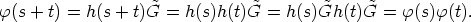
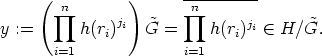
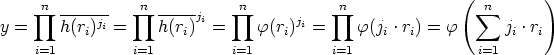
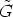
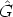 . By assumption
. By assumption 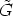 . From (2) it is clear that
. From (2) it is clear that
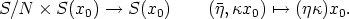


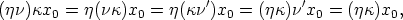
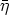 on
on 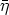 . Furthermore, it is clear that
. Furthermore, it is clear that 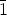
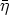
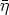
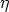
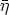
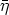
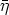
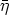
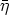
 x
x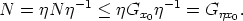
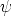
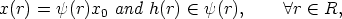
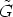 ,
and
,
and 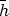 (
(