Generalizations of the functional equation of the
mean sun
HARALD FRIPERTINGER*
LUDWIG REICH
1 Introduction
Local solar time is measured by a sundial. When the center of the sun is on an observer’s
meridian, the observer’s local solar time is zero hours (noon). Because the earth moves with
varying speed in its orbit at different times of the year and because the plane of the earth’s
equator is inclined to its orbital plane, the length of the solar day is different depending on the
time of year. It is more convenient to define time in terms of the average of local solar time.
Such time, called mean solar time, may be thought of as being measured relative to an
imaginary sun (the mean sun) that lies in the earth’s equatorial plane and about
which the earth orbits with constant speed. Every mean solar day is of the same
length.1
In [1, 4] it is shown that the mean sun satisfies the functional equation
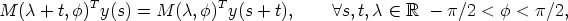 | (1) |
where y(s) is a vector of length 1, which is the direction from the center of the
earth to the sun at the time s (one day corresponds to 2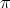 ) expressed in a geocentric
coordinate system. As a basis of this system we can choose two orthogonal vectors
in the equatorial plane and one vector along the axis of the earth. M(
) expressed in a geocentric
coordinate system. As a basis of this system we can choose two orthogonal vectors
in the equatorial plane and one vector along the axis of the earth. M( ,
, 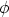 ) is the
matrix
) is the
matrix
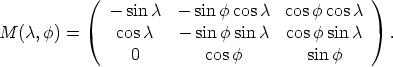
Then M( ,
, 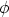 )y(s) is the direction from the earth to the sun expressed in a local
coordinate system on the surface of the earth in the point of longitude
)y(s) is the direction from the earth to the sun expressed in a local
coordinate system on the surface of the earth in the point of longitude  and latitude
and latitude
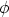 .
.
In the present paper we investigate generalizations of equation (1) for fixed 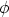 . To be more
precise, first we will solve the following functional equation
. To be more
precise, first we will solve the following functional equation
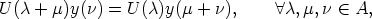 | (2) |
where (A, +) is an Abelian group, K is a field, n is a positive integer, and both y: A  Kn
and U: A
Kn
and U: A  GL(n, K) are unknown functions, which will be determined by (2). In some
situations we will additionally have to assume that A = K. Later on we will study the more
general situation when we replace GL(n, k) by Mn(K), the set of all n × n matrices over
K.
The following types of questions can be asked in connection with (2):
GL(n, K) are unknown functions, which will be determined by (2). In some
situations we will additionally have to assume that A = K. Later on we will study the more
general situation when we replace GL(n, k) by Mn(K), the set of all n × n matrices over
K.
The following types of questions can be asked in connection with (2):
- Determine all solutions (U, y) of (2).
- For given U determine all y, such that (U, y) is a solution of (2).
- For given y determine all U, such that (U, y) is a solution of (2).
- Find relations between U and y for a solution (U, y) of (2).
We will mainly deal with problems of the second and third kind.
In Theorem 6 we describe in an appropriate system of coordinates the structure of the
space SU of all solutions of (2) for a given U: A  GL(n, K). We also state in this theorem
how such a mapping U necessarily looks if a nontrivial solution y (i.e. y
GL(n, K). We also state in this theorem
how such a mapping U necessarily looks if a nontrivial solution y (i.e. y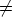 0) exists. A similar
description of U-invariant subspaces of SU is given in Theorem 8. We emphasize that by our
result (and similarly by the following theorems) the problem of solving (2) can be reduced, at
least to some extent, to the problem of finding all exponential functions U11: A
0) exists. A similar
description of U-invariant subspaces of SU is given in Theorem 8. We emphasize that by our
result (and similarly by the following theorems) the problem of solving (2) can be reduced, at
least to some extent, to the problem of finding all exponential functions U11: A  GL(k, K)
(cf. the representation of U in Theorem 6), i.e. non singular matrices U11(
GL(k, K)
(cf. the representation of U in Theorem 6), i.e. non singular matrices U11( ) satisfying the
equation
) satisfying the
equation
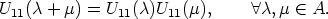
Here we assume that these functions are known and we refer the reader to [3].
In Theorem 9 we construct to a given subspace S0 of Kn the set of all mappings U and
correspondingly the space S of all functions y, such that (U, y) satisfies (2) and
S0 is exactly the set of all initial values y(0) for y  S. It is clear that this yields
together with Theorem 6 an implicit description of the set of all solutions (U, y) of
(2) by varying the subspace S0 of Kn. However, the space S and the mapping U
obtained in this way from S0 may have the property that S is a proper subset of
SU . Therefore we also deal with the problem to characterize the situation when
S = SU .
S. It is clear that this yields
together with Theorem 6 an implicit description of the set of all solutions (U, y) of
(2) by varying the subspace S0 of Kn. However, the space S and the mapping U
obtained in this way from S0 may have the property that S is a proper subset of
SU . Therefore we also deal with the problem to characterize the situation when
S = SU .
From a mathematical point of view it seems also interesting to study the functional
equation (2) for mappings U: A  Mn(K). This situation is more complicated both with
respect to the technical details and the construction (description) of the solutions U or
y or (U, y). In Theorem 20 we start from a given mapping U: A
Mn(K). This situation is more complicated both with
respect to the technical details and the construction (description) of the solutions U or
y or (U, y). In Theorem 20 we start from a given mapping U: A  Mn(K) and
describe completely in appropriate coordinates the set of all functions y: A
Mn(K) and
describe completely in appropriate coordinates the set of all functions y: A  Kn, such
that (U, y) is a solution of (2). Again this theorem provides necessary conditions
on U for the existence of nontrivial solutions y of (2). We also show in Theorem
21 how to construct all mappings U: A
Kn, such
that (U, y) is a solution of (2). Again this theorem provides necessary conditions
on U for the existence of nontrivial solutions y of (2). We also show in Theorem
21 how to construct all mappings U: A  Mn(K) and corresponding spaces S of
functions y: A
Mn(K) and corresponding spaces S of
functions y: A  Kn, such that
Kn, such that 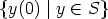 is a given subspace S0 of Kn and (U, y)
is a solution of (2), hence giving an implicit description of the general solution of
(2) by varying S0. However, we were not able to contribute to the problem when
S = SU .
is a given subspace S0 of Kn and (U, y)
is a solution of (2), hence giving an implicit description of the general solution of
(2) by varying S0. However, we were not able to contribute to the problem when
S = SU .
The main difficulties in this last part seem to arise from the fact that there can occur
solutions y (to a given U) with y(0) = 0 but y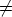 0 (cf. Lemma 18).
0 (cf. Lemma 18).
2 Regular matrices U( )
)
Here in this part we always assume that U is a mapping from the abelian group A to
GL(n, K).
Lemma 1. Let B, C be matrices in GL(n, k). Then (U, y) is a solution of (2) if and
only if (V, By) is a solution of (2), where V ( ) = CU(
) = CU( )B-1.
)B-1.
-
- Proof. The pair (U, y) is a solution of (2) if U(
 +
+ )y(
)y( ) = U(
) = U( )y(
)y( +
+ ) for all
) for all  ,
,  ,
, 
 A. Since B and C are regular matrices, this is equivalent to CU(
A. Since B and C are regular matrices, this is equivalent to CU( +
+  )B-1By(
)B-1By( ) =
CU(
) =
CU( )B-1By(
)B-1By( +
+  ) for all
) for all  ,
,  ,
, 
 A.
A. ![[]](lasy10-c-32.gif)
For C = U(0)-1 we get CU(0) = I
n, the identity matrix. Hence, without loss of generality we
will always assume that U(0) = In.
Lemma 2. If (U, y) is a solution of (2), then
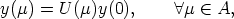 | (3) |
![[U (c + m) - U (c)U (m)]y(0) = 0, A c, m (- A.](reich_son8x.gif) | (4) |
-
- Proof. Since U(0) = In, we get (3) from (2) for
 =
=  = 0. And we get (4) from (2) and
(3) for
= 0. And we get (4) from (2) and
(3) for  = 0.
= 0. ![[]](lasy10-c-32.gif)
It is also possible to reverse the statement of Lemma 2.
Lemma 3. Assume U(0) = In and let y be given by (3). If (U, y) satisfies (4), then
(U, y) is a solution of (2).
For any mapping U: A  GL(n, k) let
GL(n, k) let
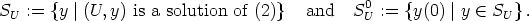
Some basic properties of these two sets are collected in the following
-
- Proof. It is clear that SU and SU0 are linear spaces. Assume that y0
 SU0, then
there is some y
SU0, then
there is some y  SU , such that y(0) = y0. Since (U, y) satisfies (3), the function
SU , such that y(0) = y0. Since (U, y) satisfies (3), the function 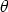 is
well defined. It is surjective, since for any y
is
well defined. It is surjective, since for any y  SU we have
SU we have 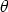 (y(0)) = U(.)y(0) = y(.)
according to (3). The mapping
(y(0)) = U(.)y(0) = y(.)
according to (3). The mapping 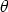 is also injective, since from
is also injective, since from 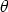 (y10) =
(y10) = 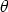 (y20) we derive
U(
(y20) we derive
U( )y10 = U(
)y10 = U( )y20, which implies for
)y20, which implies for  = 0 (and U(0) = In) that y10 = y20.
Finally we have to prove that
= 0 (and U(0) = In) that y10 = y20.
Finally we have to prove that 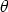 is a linear mapping. Let y10, y20
is a linear mapping. Let y10, y20  SU0 and let
SU0 and let
 1,
1,  2
2  K, then
K, then  1y10 +
1y10 +  2y20
2y20  SU0 and
SU0 and 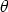 (
( 1y10 +
1y10 +  2y20) = U(.)(
2y20) = U(.)( 1y10 +
1y10 +  2y20) =
2y20) =
 1U(.)y10 +
1U(.)y10 +  2U(.)y20 =
2U(.)y20 =  1
1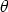 (y10) +
(y10) +  2
2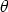 (y20).
(y20). ![[]](lasy10-c-32.gif)
In conclusion, both SU and SU0 are m-dimensional linear spaces for some 0 < m < n.
There are some more interesting properties of SU and SU0.
-
- Proof.
- Assume that z(
 ) := U(
) := U( 0)y(
0)y( ). Then (U, z) satisfies (2), since U(
). Then (U, z) satisfies (2), since U( +
+  )z(
)z( ) =
U(
) =
U( +
+  )U(
)U( 0)y(
0)y( ) = U(
) = U( +
+  )U(
)U( 0)U(
0)U( )y(0) = U(
)y(0) = U( +
+  )U(
)U( 0 +
0 +  )y(0) = U(
)y(0) = U( +
+
 )y(
)y( 0 +
0 +  ) = U(
) = U( )y(
)y( +
+  0 +
0 +  ) = U(
) = U( )U(0)y(
)U(0)y( 0 +
0 +  +
+  ) = U(
) = U( )U(
)U( 0)y(
0)y( +
+  ) =
U(
) =
U( )z(
)z( +
+  ) by (3), (4), (3), (2), special form of U(0) and (2).
) by (3), (4), (3), (2), special form of U(0) and (2).
- Let z(
 ) := y(
) := y( +
+ 0), then (U, z) satisfies (2), since U(
0), then (U, z) satisfies (2), since U( +
+ )z(
)z( ) = U(
) = U( +
+ )y(
)y( +
+
 0) = U(
0) = U( )y(
)y( +
+  +
+  0) = U(
0) = U( )z(
)z( +
+  ) by (2).
) by (2).
- If y0
 SU0, there exists some y
SU0, there exists some y  S
U , such that y0 = y(0). From the first item of
this lemma we know that U(
S
U , such that y0 = y(0). From the first item of
this lemma we know that U( 0)y
0)y  SU , hence U(
SU , hence U( 0)y(0) = U(
0)y(0) = U( 0)y0
0)y0  SU0.
SU0.
- According to the definition of SU0 we know that SU0
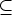
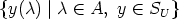 .
Let y
.
Let y  SU and assume that
SU and assume that  0
0  A \
A \ 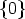 , then it follows from the second item of
this lemma that z(.) := y(. +
, then it follows from the second item of
this lemma that z(.) := y(. +  0)
0)  SU and y(
SU and y( 0) = z(0)
0) = z(0)  SU0.
SU0. ![[]](lasy10-c-32.gif)
If 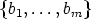 denotes a basis of SU0, then there exists a matrix B
denotes a basis of SU0, then there exists a matrix B  GL(n, k), such that
Bbi = ei, the i-th unit vector in Kn. Applying this matrix B as a coordinate transformation
on Kn as in Lemma 1 we get that SUB-1 - 1 = <e
1, ..., em>, the m-dimensional linear space
generated by the first m unit vectors in Kn. Thus without loss of generality we may assume
that SU = <e1, ..., em>.
GL(n, k), such that
Bbi = ei, the i-th unit vector in Kn. Applying this matrix B as a coordinate transformation
on Kn as in Lemma 1 we get that SUB-1 - 1 = <e
1, ..., em>, the m-dimensional linear space
generated by the first m unit vectors in Kn. Thus without loss of generality we may assume
that SU = <e1, ..., em>.
Theorem 6. Let U: A  GL(n, K) be a mapping, such that SU0 = <e1, ..., em> and
U(0) = In. Then U(
GL(n, K) be a mapping, such that SU0 = <e1, ..., em> and
U(0) = In. Then U( ) can be partitioned as a block matrix of the form
) can be partitioned as a block matrix of the form
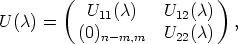
where U11( )
)  GL(m, K), U22(
GL(m, K), U22( )
)  GL(n - m, K) and U12(
GL(n - m, K) and U12( )
)  Mm,n-m(K).
These matrices satisfy the boundary conditions U11(0) = Im, U22(0) = In-m and
U12(0) = (0)m,n-m, the zero matrix. Moreover, U11 is an exponential function, i.e.
U11(
Mm,n-m(K).
These matrices satisfy the boundary conditions U11(0) = Im, U22(0) = In-m and
U12(0) = (0)m,n-m, the zero matrix. Moreover, U11 is an exponential function, i.e.
U11( +
+  ) = U11(
) = U11( )U11(
)U11( ) for all
) for all  ,
, 
 A.
A.
Each y  SU can be expressed as
SU can be expressed as
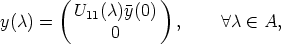
and 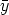 (0)
(0)  Km.
Km.
-
- Proof. Let y
 SU , then y(
SU , then y( )
)  SU0 = <e1, ..., em>, so y(
SU0 = <e1, ..., em>, so y( ) =
) = 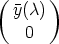 and
and 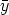 (
( )
)  Km. We
partition U(
Km. We
partition U( ) as a block matrix
) as a block matrix
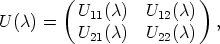 | (5) |
such that U11( ) is an m × m-matrix. From (3) we deduce that Since
) is an m × m-matrix. From (3) we deduce that Since 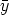 (0) is an arbitrary element of Km, it is clear that U
21(
(0) is an arbitrary element of Km, it is clear that U
21( ) = (0)n-m,m for all
) = (0)n-m,m for all 
 A.
Because of the fact that U(
A.
Because of the fact that U( ) is regular, both U11 and U22 are regular matrices as well. From
U(0) = In the boundary conditions follow. Inserting into (4) the form of U and y just
described we get
) is regular, both U11 and U22 are regular matrices as well. From
U(0) = In the boundary conditions follow. Inserting into (4) the form of U and y just
described we get
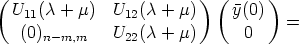
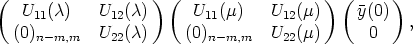
which means that U11( +
+  )
)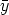 (0) = U11(
(0) = U11( )U11(
)U11( )
)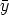 (0) for all
(0) for all 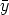 (0)
(0)  Km and
Km and  ,
, 
 A, so that
U11 is an exponential function.
A, so that
U11 is an exponential function. ![[]](lasy10-c-32.gif)
We are also interested in subspaces of SU . First we present a generalization of Lemma 5.
-
- Proof. In order to prove that 1 implies 2, we set z(
 ) := y(
) := y( +
+  0) for arbitrary
0) for arbitrary  0
0  A.
Since S is U(
A.
Since S is U( 0)-invariant, U(
0)-invariant, U( 0)y
0)y  S. It is enough to prove that z = U(
S. It is enough to prove that z = U( 0)y, since
then z
0)y, since
then z  S. For
S. For 
 A we get z(
A we get z( ) = y(
) = y( 0 +
0 +  ) = U(
) = U( 0 +
0 +  )y(0) = U(
)y(0) = U( 0)U(
0)U( )y(0) =
U(
)y(0) =
U( 0)y(
0)y( ), so z = U(
), so z = U( 0)y by (3), (4) and (3).
0)y by (3), (4) and (3).
To each y0  S0 there exists y
S0 there exists y  S, such that y0 = y(0). Under the assumption 2,
the function z(
S, such that y0 = y(0). Under the assumption 2,
the function z( ) := y(
) := y( +
+  0) belongs to S for any
0) belongs to S for any  0
0  A. So z(0)
A. So z(0)  S0 and
z(0) = y(
S0 and
z(0) = y( 0) = U(
0) = U( 0)y(0) = U(
0)y(0) = U( 0)y0 by (3). Thus we proved that 2 implies 3.
0)y0 by (3). Thus we proved that 2 implies 3.
In order to close the cycle of implications take y  S. Then y(0)
S. Then y(0)  S0. For
arbitrary
S0. For
arbitrary  0
0  A also U(
A also U( 0)y(0) belongs to S0. Hence, there exists z
0)y(0) belongs to S0. Hence, there exists z  S such that
z(0) = U(
S such that
z(0) = U( 0)y(0). Taking into account that S is a subspace of SU we can write z as
z(
0)y(0). Taking into account that S is a subspace of SU we can write z as
z( ) = U(
) = U( )z(0) = U(
)z(0) = U( )U(
)U( 0)y(0) = U(
0)y(0) = U( +
+  0)y(0) = U(
0)y(0) = U( 0)U(
0)U( )y(0) = U(
)y(0) = U( 0)y(
0)y( ) by
(3), (4), (4) and (3). Thus U(
) by
(3), (4), (4) and (3). Thus U( 0)y
0)y  S.
S. ![[]](lasy10-c-32.gif)
A generalization of Theorem 6 is
Theorem 8. Let S be a k-dimensional U-invariant subspace of SU . Then there exist
coordinates in Kn, such that S0 = <e
1, ..., ek>, and U( ) is a block matrix of the form
) is a block matrix of the form
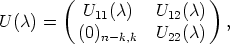 | (6) |
where U11(

)

GL(
k, K)
, U22(

)

GL(
n - k, K)
and U12(

)
 Mk,n-k
Mk,n-k(
K)
, such that
U11(0) =
Ik, U22(0) =
In-k, U12(0) = (0)
k,n-k. Moreover, U11 is an exponential function, and
y  S if and only if
S if and only if
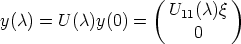
for 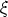
 Kk.
Kk.
So far we described solutions (U, y) of (2) when the mapping U was given. Now we will assume
that a linear subspace S0 of Kn is given and we describe all solutions (U, y) of (2), such that
SU0 = S0. Let S0 be a k-dimensional U-invariant subspace of Kn, then without loss of
generality S0 = <e
1, ..., ek>.
Theorem 9. Let S0 = <e
1, ..., ek> be a subspace of Kn, and let U
11( )
)  GL(k, K),
U22(
GL(k, K),
U22( )
)  GL(n - k, K) and U12(
GL(n - k, K) and U12( )
)  Mk,n-k(K), such that U11(0) = Ik, U22(0) = In-k,
U12(0) = (0)k,n-k. Moreover U11 is assumed to be an exponential function. Then
Mk,n-k(K), such that U11(0) = Ik, U22(0) = In-k,
U12(0) = (0)k,n-k. Moreover U11 is assumed to be an exponential function. Then
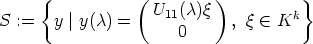
is a U-invariant subspace of SU , where U is given by (6).
-
- Proof.
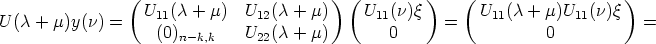
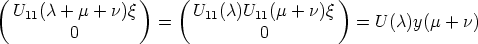
![[]](lasy10-c-32.gif)
When does S = SU hold?
-
- Proof. From Lemma 2 and Lemma 3 we know that S is a subspace of SU different from
SU if and only if there exists y0 /
 S0, such that [U(
S0, such that [U( +
+  ) - U(
) - U( )U(
)U( )]y0 = 0 for all
)]y0 = 0 for all
 ,
, 
 A. In other words, S = SU if and only if for each y0 /
A. In other words, S = SU if and only if for each y0 / S0 there exists (
S0 there exists ( 0,
0,  0)
0)  A2,
such that [U(
A2,
such that [U( 0+
0+ 0)-U(
0)-U( 0)U(
0)U( 0)]y0
0)]y0 0. When writing y0 in the form
0. When writing y0 in the form  for
for 
 Kk
and
Kk
and 
 Kn-k, then y0
Kn-k, then y0  Kn \ S0 if and only if
Kn \ S0 if and only if 
 0. Together with (6) we get
0. Together with (6) we get
![( )
0 [U11(c)U12(m) + U12(c)U22(m) - U12(c + m)]j
[U (c + m) - U (c)U (m)]y = [U22(c)U22(m) - U22(c + m)]j ,](reich_son38x.gif)
which finishes the proof. ![[]](lasy10-c-32.gif)
Now we are going to present several examples for the situation S = SU , i.e. by Lemma 10
examples, where condition (7) is satisfied. Here we always assume that A = K. First we will
deal with the second line of condition (7). Secondly, if this condition is not satisfied by all  ,
then let V denote the set
,
then let V denote the set
![{j (- Kn -k |[U22(c)U22(m) - U22(c + m)]j = 0, A c,m (- A} .](reich_son39x.gif)
Thus V is an r-dimensional subspace of Kn-k for 0 < r < n - k. In order to satisfy the
requirements of Lemma 10 in this situation as well, the first line in (7) must be satisfied for

 V .
V .
Now we describe some examples how to construct U22: K  GL(s, K) for s < n - k, such
that
GL(s, K) for s < n - k, such
that
![A j (- Ks \{0} E c ,m (- K : [U (c )U (m ) - U (c + m )]j /= 0.
0 0 22 0 22 0 22 0 0](reich_son40x.gif) | (8) |
-
Case charK
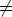 2:
2: - Set U22(
 ) = cIs for all
) = cIs for all 
 K \
K \ 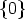 with c
with c  K \
K \ 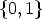 . Then c2
. Then c2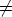 c.
For
c.
For  0 =
0 =  0 = 1 we get [U22(1)U22(1)-U22(1+1)]
0 = 1 we get [U22(1)U22(1)-U22(1+1)] = [c2I
s -cIs]
= [c2I
s -cIs] = (c2-c)I
s
= (c2-c)I
s
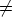 0
for all
0
for all 
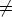 0.
0.
-
Case charK = 2 and
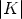 > 2:
> 2: - There exists c
 K\
K\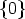 , such that c2
, such that c2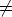 1. Let U
22(
1. Let U
22( ) =
cIs for all
) =
cIs for all 
 K \
K \ 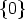 , then for
, then for  0 =
0 =  0 = 1 we get [U22(1)U22(1) - U22(1 + 1)]
0 = 1 we get [U22(1)U22(1) - U22(1 + 1)] =
[U22(1)2 - U
22(0)]
=
[U22(1)2 - U
22(0)] = [c2I
s - Is]
= [c2I
s - Is] = (c2 - 1)I
s
= (c2 - 1)I
s
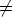 0 for all
0 for all 
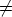 0.
0.
-
Case
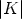 = 2:
= 2: - If s = 1 each mapping U22: K
 GL(1, K) =
GL(1, K) = 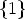 is a homomorphism,
so (8) cannot be satisfied. If s > 1 there exist matrices M
is a homomorphism,
so (8) cannot be satisfied. If s > 1 there exist matrices M  GL(s, K) of order 2s-1.
As a permutation of the vectors in Ks the cycle decomposition of M consists of one
fixed point, the 0-vector, and a cycle of length 2s-1. (Actually, cf. [2] 3.5 Theorem,
there are
GL(s, K) of order 2s-1.
As a permutation of the vectors in Ks the cycle decomposition of M consists of one
fixed point, the 0-vector, and a cycle of length 2s-1. (Actually, cf. [2] 3.5 Theorem,
there are 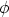 (2s - 1)/s irreducible polynomials of degree s over K = GF (2), such
that the companion matrix of these polynomials is of order 2s - 1.) If U
22(1) = M,
then for
(2s - 1)/s irreducible polynomials of degree s over K = GF (2), such
that the companion matrix of these polynomials is of order 2s - 1.) If U
22(1) = M,
then for  0 =
0 =  0 = 1 we get [U22(1)U22(1) - U22(1 + 1)]
0 = 1 we get [U22(1)U22(1) - U22(1 + 1)] = [M2 - I
s]
= [M2 - I
s]
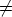 0 for all
0 for all

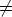 0, since 2 < 2s - 1.
0, since 2 < 2s - 1.
Now we describe examples how to construct U12: K  Mk,n-k(K), such that
Mk,n-k(K), such that
![A j (- Kn -k\{0} E c0,m0 (- K : [U11(c0)U12(m0) + U12(c0)U22(m0) - U12(c0 + m0)]j /= 0.](reich_son57x.gif) | (9) |
Again we assume that A = K. Furthermore we assume that both U11 and U22 are exponential
functions. Hence r = n - k. From the preceding considerations we already know that
U11( )
)  GL(k, K), U22(
GL(k, K), U22( )
)  GL(r, K), U11(0) = Ik, U22(0) = Ir and U12(0) = (0)k,r. Again
we describe several different cases:
GL(r, K), U11(0) = Ik, U22(0) = Ir and U12(0) = (0)k,r. Again
we describe several different cases:
-
Case charK
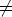 2:
2: - If k > r, then assume that U12(1) = (0)k,r and
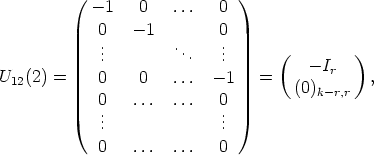
where the upper part is -Ir and the lower part is a 0-matrix of the dimension
(k - r) × r. Then for  0 =
0 =  0 = 1 we get that U11(1)U12(1) + U12(1)U22(1) -
U12(1 + 1) = -U12(2) and it is obvious that -U12(2)
0 = 1 we get that U11(1)U12(1) + U12(1)U22(1) -
U12(1 + 1) = -U12(2) and it is obvious that -U12(2)
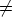 0 for all
0 for all 
 Kr \
Kr \  .
.
For k < r one possible way to proceed is indicated in
-
- Proof. There exist uniquely determined integers q, s, such that r = kq + s and
0 < s < k. If q > 0 assume that
 1
1  K \
K \  , then -
, then - 1
1  K \
K \ 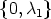 . Let
U12(±
. Let
U12(± 1) be given by
1) be given by
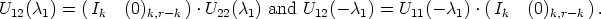
If q > 1 and 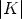 is big enough, then there exists
is big enough, then there exists  2
2  K \
K \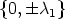 and we assume
that
and we assume
that
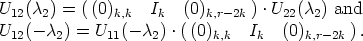
Going on like this we can find elements  1, ...,
1, ...,  q
q  K and matrices U12(±
K and matrices U12(± i). If
s > 0 and
i). If
s > 0 and 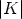 is big enough, then there exists
is big enough, then there exists  q+1
q+1  K \
K \ 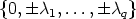 and
we assume that
and
we assume that
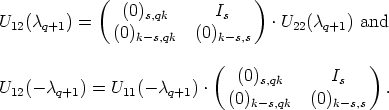
When 
 Kr \
Kr \  , then there exists 1 < i < r, such that
, then there exists 1 < i < r, such that  i
i 0. Hence, there
exists j
0. Hence, there
exists j 
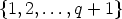 , such that (j - 1)k < i < jk. For
, such that (j - 1)k < i < jk. For  0 =
0 =  j and
j and  0 =
-
0 =
- j we have U11(
j we have U11( j)U12(-
j)U12(- j) + U12(
j) + U12( j)U22(-
j)U22(- j) - U12(0) = 2U12(
j) - U12(0) = 2U12( j)U22(-
j)U22(- j).
According to the choice of i and j it is clear that (9) is satisfied.
j).
According to the choice of i and j it is clear that (9) is satisfied. ![[]](lasy10-c-32.gif)
This is a very general result, but it is not the best result which is possible.
Example 12. Let K be the prime field of characteristic 3, k = 1 and r = 2. In this
case 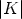 < 2
< 2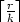 + 1, but it is also possible to find U12, such that (9) is satisfied.
For instance U given by
+ 1, but it is also possible to find U12, such that (9) is satisfied.
For instance U given by
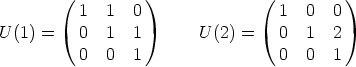
satisfies (9).
-
Case charK = 2 and
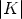 > 2:
> 2: - Assume first k > r. There exists

 K \
K \ 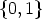 and then
and then
 + 1 /
+ 1 /
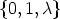 . Let furthermore U12(1) = U12(
. Let furthermore U12(1) = U12( ) = (0)k,r and
) = (0)k,r and
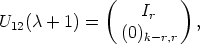
then for  0 = 1 and
0 = 1 and  0 =
0 =  we get U11(1)U12(
we get U11(1)U12( ) + U12(1)U22(
) + U12(1)U22( ) - U12(
) - U12( + 1) = U12(
+ 1) = U12( + 1)
and (9) is satisfied. For k < r the following lemma holds:
+ 1)
and (9) is satisfied. For k < r the following lemma holds:
-
- Proof. There exist uniquely determined integers q, s, such that r = kq + s
and 0 < s < k. Assume U12(1) = (0)k,r. For 1 < i < q there exists
 i
i  K \
K \ 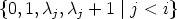 , such that
, such that  i + 1 /
i + 1 /
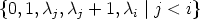 . Let
U12(
. Let
U12( i) and U12(
i) and U12( i + 1) be given by
i + 1) be given by
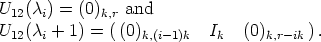
If s > 0 and 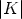 is big enough, then there exists
is big enough, then there exists  q+1
q+1  K, such that
K, such that
 q+1,
q+1,  q+1 + 1
q+1 + 1  K \
K \ 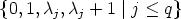 and we assume that
and we assume that
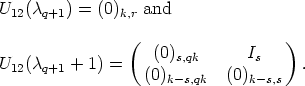
Given 
 Kr \
Kr \ 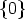 there exists 1 < i < r, such that
there exists 1 < i < r, such that  i
i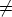 0. Hence, there exists
j
0. Hence, there exists
j 
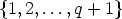 , such that (j - 1)k < i < jk. For
, such that (j - 1)k < i < jk. For  0 =
0 =  j and
j and  0 = 1 we have
U11(
0 = 1 we have
U11( j)U12(1) + U12(
j)U12(1) + U12( j)U22(1) - U12(
j)U22(1) - U12( j + 1) = -U12(
j + 1) = -U12( j + 1). According to the
choice of i and j it is clear that (9) is satisfied.
j + 1). According to the
choice of i and j it is clear that (9) is satisfied. ![[]](lasy10-c-32.gif)
-
Case
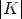 = 2:
= 2: - In the situation r > k we can only give partial results. If
 0 = 0 or
0 = 0 or  0 = 0,
then it is impossible to satisfy (9). Since U11 and U22 are exponential functions, the
orders of U11(1) and U22(1) are divisors of 2. If both U11(1) = Ik and U22(1) = Ir, then
it is also impossible to satisfy (9). If r = 1, then U22(1) is the identity matrix I1. From
the previous statements it is clear that necessarily k > 1 and U11(1) must be a matrix of
order 2. If U is defined by
0 = 0,
then it is impossible to satisfy (9). Since U11 and U22 are exponential functions, the
orders of U11(1) and U22(1) are divisors of 2. If both U11(1) = Ik and U22(1) = Ir, then
it is also impossible to satisfy (9). If r = 1, then U22(1) is the identity matrix I1. From
the previous statements it is clear that necessarily k > 1 and U11(1) must be a matrix of
order 2. If U is defined by
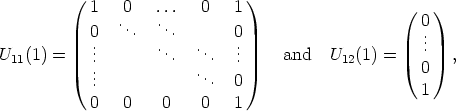
then (9) is satisfied. For r = 2 assume that U11(1) is given as above and
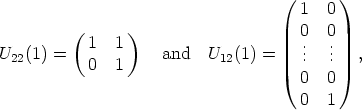
then again (9) is satisfied. For k = r = 3 and for any choice of U11(1), U22(1)  GL(3, K) of
order dividing 2 the computer did not find a matrix U12(1) in M3(K) such that (9) is
satisfied. Other cases were not studied so far.
GL(3, K) of
order dividing 2 the computer did not find a matrix U12(1) in M3(K) such that (9) is
satisfied. Other cases were not studied so far.
If k > r it is not possible to satisfy (9), since there is only one possible choice
 0 =
0 =  0 = 1, which determines exactly one matrix U11(1)U12(1) + U12(1)U22(1). This
matrix describes a homomorphism from Kk to Kr, which has a kernel of dimension
> k - r > 0.
0 = 1, which determines exactly one matrix U11(1)U12(1) + U12(1)U22(1). This
matrix describes a homomorphism from Kk to Kr, which has a kernel of dimension
> k - r > 0.
3 The general situation
In this part we generalize the functional equation (2) by assuming that U( ) is not necessarily
a regular matrix, i.e. U: A
) is not necessarily
a regular matrix, i.e. U: A  Mn(K). Also in this situation Lemma 1 holds. When we define
SU and SU0 as it was done earlier, then SU and SU0 are K-linear spaces (cf. Lemma 4). Again
SU0 is an m-dimensional subspace of Kn for 0 < m < n, and S
U is invariant under
translations, and SU0 =
Mn(K). Also in this situation Lemma 1 holds. When we define
SU and SU0 as it was done earlier, then SU and SU0 are K-linear spaces (cf. Lemma 4). Again
SU0 is an m-dimensional subspace of Kn for 0 < m < n, and S
U is invariant under
translations, and SU0 = 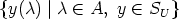 (cf. Lemma 5). Without loss of generality
we can assume (as in the earlier case) that there exists a basis of Kn, such that
SU0 = <e1, ..., em>.
(cf. Lemma 5). Without loss of generality
we can assume (as in the earlier case) that there exists a basis of Kn, such that
SU0 = <e1, ..., em>.
Since U(0) need not be a regular matrix, we do not get the results of Lemma 2, and in
general there is no isomorphism between SU and SU0.
For  =
=  = 0 or
= 0 or  = 0 we derive from (2)
= 0 we derive from (2)
Lemma 14. Let (U, y) be a solution of (2), then
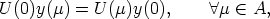 | (10) |
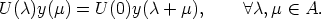 | (11) |
If U( ) is partitioned as in (5) and y(
) is partitioned as in (5) and y( ) is written as
) is written as 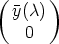 for
for 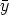 (
( )
)  Km, then from (10)
we get
Km, then from (10)
we get
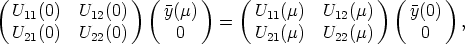
which leads to the system of equations
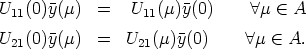 | (12) |
Lemma 15. Let (U, y) be a solution of (2). Then there exists a system of coordinates of Kn,
such that
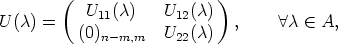 | (13) |
where the m × m-matrix U11(0)
is the block matrix of the form
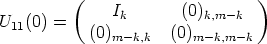 | (14) |
for some k < m.
-
- Proof. According to Lemma 1 choose matrices C
 GL(n, K) and B'
GL(n, K) and B'  GL(m, K), such
that
GL(m, K), such
that
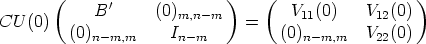
and
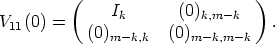
Without loss of generality assume that U = V . From the second line of (12) we deduce
that 0 = 0 (
( ) = U21(
) = U21( )
)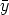 (0) for all
(0) for all 
 A. Since
A. Since 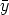 (0) can arbitrarily be chosen in Km,
it is clear that U21(
(0) can arbitrarily be chosen in Km,
it is clear that U21( ) = (0)n-m,m for all
) = (0)n-m,m for all 
 A.
A. ![[]](lasy10-c-32.gif)
Since SU0 = <e1, ..., em>, there exist y1, ..., ym  SU , such that yj(0) = ej, the j-th unit
vector in Kn, for 1 < j < m. Let S
U ' := <y
1, ..., ym>, then SU ' is an m-dimensional subspace of
SU . In order to prove this, it is only necessary to show that y1, ..., ym are linearly independent.
Let
SU , such that yj(0) = ej, the j-th unit
vector in Kn, for 1 < j < m. Let S
U ' := <y
1, ..., ym>, then SU ' is an m-dimensional subspace of
SU . In order to prove this, it is only necessary to show that y1, ..., ym are linearly independent.
Let  1, ...,
1, ...,  m
m  K, such that
K, such that 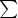 i = 1m
i = 1m iyi = 0, then also
iyi = 0, then also 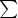 i = 1m
i = 1m iyi(0) = 0, which
implies
iyi(0) = 0, which
implies 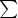 i = 1m
i = 1m iei = 0, so that
iei = 0, so that  1 = ... =
1 = ... =  m = 0.
m = 0.
For y  SU ' there exist uniquely defined
SU ' there exist uniquely defined  1, ...,
1, ...,  m
m  K such that y =
K such that y = 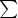 i = 1m
i = 1m iyi. These
iyi. These
 i can be read from y(0), since y(0) =
i can be read from y(0), since y(0) = 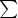 i = 1m
i = 1m iei.
iei.
Define the m × m-matrix Y ( ) corresponding to the chosen y1, ..., ym by
) corresponding to the chosen y1, ..., ym by
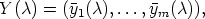 | (15) |
i.e. the j-th column of Y ( ) is the vector
) is the vector 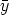 j(
j( )
)  Km. Then for y
Km. Then for y  S
U ' we have
S
U ' we have
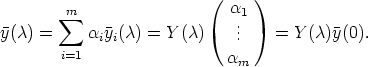 | (16) |
Replacing y by yj in the first line of (12) we get for all 
 A
A
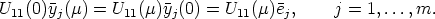
These equations are collected to the matrix equation
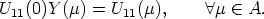 | (17) |
The special form of U from Lemma 15 inserted into (11) yields for y = yj the equation
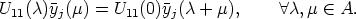
Again these equations can be collected for j = 1, ..., m and we derive
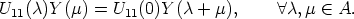 | (18) |
Equations (17) and (18) together yield
![U11(0)[Y (c + m)- Y (c)Y (m)] = (0)m,m, A c,m (- A.](reich_son118x.gif) | (19) |
According to the special form of U11(0) described in Lemma 15 we partition Y ( ) as a block
matrix
) as a block
matrix
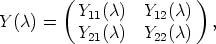
such that Y 11( ) is a k × k-matrix. We note that the “auxiliary” matrix function
Y : A
) is a k × k-matrix. We note that the “auxiliary” matrix function
Y : A  Mm(K), which will help us to describe the space SU of solutions y (for given U), is in
general not uniquely determined. However, from (17), from the decomposition of U11(0) in
Lemma 15 and the corresponding decomposition of Y (
Mm(K), which will help us to describe the space SU of solutions y (for given U), is in
general not uniquely determined. However, from (17), from the decomposition of U11(0) in
Lemma 15 and the corresponding decomposition of Y ( ) we see that Y 11(
) we see that Y 11( ) and Y 12(
) and Y 12( ) are
uniquely determined by U11(
) are
uniquely determined by U11( ), namely
), namely
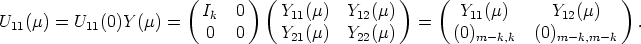 | (20) |
Then (19) can be rewritten as
![( )[( ) ( )( )]
Ik 0 Y11(c + m) Y12(c + m) - Y11(c) Y12(c) Y11(m) Y12(m) = (0)
0 0 Y21(c + m) Y22(c + m) Y21(c) Y22(c) Y21(m) Y22(m) m,m](reich_son121x.gif)
and we end up with the system of equations
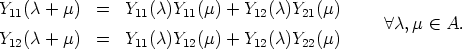 | (21) |
From Y (0) = Im we deduce that Y 11(0) = Ik, Y 21(0) = (0)m-k,k, Y 12(0) = (0)k,m-k
and Y 22(0) = Im-k. If  is replaced by
is replaced by  1 +
1 +  2 and taking into account
that + is an associative composition we get from the first line of (21) that
Y 11(
2 and taking into account
that + is an associative composition we get from the first line of (21) that
Y 11( +(
+( 1+
1+ 2)) = Y 11(
2)) = Y 11( )Y 11(
)Y 11( 1+
1+ 2)+Y 12(
2)+Y 12( )Y 21(
)Y 21( 1+
1+ 2) = Y 11(
2) = Y 11( )[Y 11(
)[Y 11( 1)Y 11(
1)Y 11( 2)+Y 12(
2)+Y 12( 1)Y 21(
1)Y 21( 2)]+Y 12(
2)]+Y 12( )Y 21(
)Y 21( 1+
1+ 2)
is equal to Y 11((
2)
is equal to Y 11(( +
+  1) +
1) +  2) = Y 11(
2) = Y 11( +
+  1)Y 11(
1)Y 11( 2) + Y 12(
2) + Y 12( +
+  1)Y 21(
1)Y 21( 2) =
[Y 11(
2) =
[Y 11( )Y 11(
)Y 11( 1) + Y 12(
1) + Y 12( )Y 21(
)Y 21( 1)]Y 11(
1)]Y 11( 2) + [Y 11(
2) + [Y 11( )Y 12(
)Y 12( 1) + Y 12(
1) + Y 12( )Y 22(
)Y 22( 1)]Y 21(
1)]Y 21( 2), which
yields
2), which
yields
![Y12(c)[Y21(m1 + m2) - Y21(m1)Y11(m2) - Y22(m1)Y21(m2)] = 0, A c, m1,m2 (- A.](reich_son123x.gif) | (22) |
In the same way we can derive from the second line of (21) that
![Y12(c)[Y22(m1 + m2) - Y21(m1)Y12(m2) - Y22(m1)Y22(m2)] = 0, A c, m1,m2 (- A.](reich_son124x.gif) | (23) |
Each Y 12( ) determines a homomorphism from Km-k to Kk. Let W :=
) determines a homomorphism from Km-k to Kk. Let W := 

 A ker Y 12(
A ker Y 12( ).
Then W is an r-dimensional subspace of Km-k for 0 < r < m - k with basis
).
Then W is an r-dimensional subspace of Km-k for 0 < r < m - k with basis 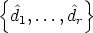 .
Moreover, there exists an m - k - r-dimensional subspace V of Km-k, such that
Km-k = V
.
Moreover, there exists an m - k - r-dimensional subspace V of Km-k, such that
Km-k = V 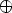 W . Let
W . Let 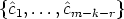 be a basis of V . We embed Km-k in a natural way into
Km by placing k zeros in front of each vector, i.e.
be a basis of V . We embed Km-k in a natural way into
Km by placing k zeros in front of each vector, i.e.
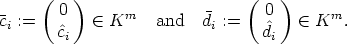
Then it is possible to find a matrix B''  GL(m - k, K), such that the coordinate
transformation on Km induced by
GL(m - k, K), such that the coordinate
transformation on Km induced by
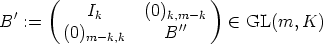
satisfies
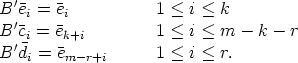
Let B be the corresponding coordinate transformation on Kn
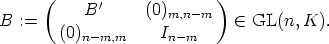
If U is decomposed as in (13) and (14), then also UB has this property.
Without loss of generality we assume that the basis of Kn was chosen in such a way that
Lemma 15 is satisfied and that 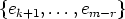 and
and 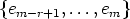 are a basis of V or W
respectively. Then it is useful and important to partition Y (
are a basis of V or W
respectively. Then it is useful and important to partition Y ( ) further as a 3 × 3 block matrix
of the form
) further as a 3 × 3 block matrix
of the form
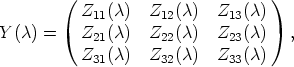
such that Z11( ) = Y 11(
) = Y 11( )
)  Mk(K), Z22(
Mk(K), Z22( )
)  Mm-k-r(K) and Z33(
Mm-k-r(K) and Z33( )
)  Mr(K).
Hence
Mr(K).
Hence
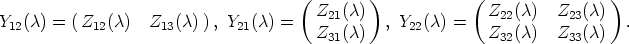
Let x = 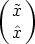 denote a vector in Km-k, where
denote a vector in Km-k, where 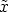
 Km-k-r and
Km-k-r and 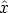
 Kr. Then x belongs to
W if and only if
Kr. Then x belongs to
W if and only if 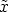 = 0. Moreover Y 12(
= 0. Moreover Y 12( )|W = 0 for all
)|W = 0 for all 
 A, which means Z13(
A, which means Z13( ) = (0)k,r for
all
) = (0)k,r for
all 
 A. From the definition of W it is clear that Z12(
A. From the definition of W it is clear that Z12( )
)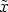 = 0 for all
= 0 for all 
 A is equivalent to
A is equivalent to
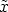 = 0.
= 0.
The first line of (21) reads now as
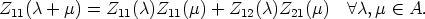
From the second line of (21) we derive
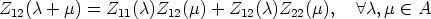
and
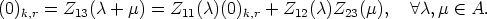
Hence, each column of Z23( ) is 0
) is 0  Km-k-r, so that Z
23(
Km-k-r, so that Z
23( ) = (0)m-k-r,m-k-r for all
) = (0)m-k-r,m-k-r for all

 A.
A.
From (22) we deduce
![Z12(c)[Z21(m1 + m2) - Z21(m1)Z11(m2) - Z22(m1)Z21(m2)] = (0)k,k, A c,m1, m2 (- A.](reich_son144x.gif)
Let M denote the matrix between the two braces [ and ], then each column of M is
0  Km-k-r and consequently M = (0)
m-k-r,k. Hence, we proved that
Km-k-r and consequently M = (0)
m-k-r,k. Hence, we proved that
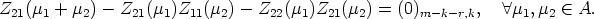
The same way we deduce from (23) that
![Z12(c)[Z22(m1 + m2) - Z21(m1)Z12(m2) - Z22(m1)Z22(m2)] = (0)k,m -k-r, A c, m1,m2 (- A](reich_son146x.gif)
and correspondingly
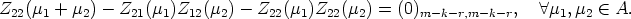
This finishes the proof of
Theorem 16. There exists a coordinate system of Km, such that Y ( ) is a solution of
(19) if and only if Y (
) is a solution of
(19) if and only if Y ( ) can be written as
) can be written as
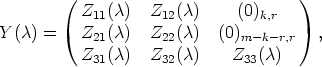
where
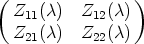
is an exponential function, Z11( )
)  Mk(K), Z22(
Mk(K), Z22( )
)  Mm-k-r(K), Z33(
Mm-k-r(K), Z33( )
)  Mr(K),
satisfying the conditions Z11(0) = Ik, Z22(0) = Im-k-r, Z33(0) = Ir, Z12(0) =
(0)k,m-k-r, Z21(0) = (0)m-k-r,k, Z31(0) = (0)r,k and Z32(0) = (0)r,m-k-r. For
Mr(K),
satisfying the conditions Z11(0) = Ik, Z22(0) = Im-k-r, Z33(0) = Ir, Z12(0) =
(0)k,m-k-r, Z21(0) = (0)m-k-r,k, Z31(0) = (0)r,k and Z32(0) = (0)r,m-k-r. For 
 0 the
matrices Z31(
0 the
matrices Z31( ), Z32(
), Z32( ), Z33(
), Z33( ) can be arbitrarily chosen.
) can be arbitrarily chosen.
Next we describe the structure of SU in more details.
-
- Proof. Since y(0)
 0 also
0 also  (0)
(0)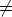 0. Hence there exist z20, ..., zm0
0. Hence there exist z20, ..., zm0  Kn, such that
Kn, such that
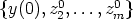 is a basis of SU0 = <e1, ..., em>. Consequently, there exist z2, ..., zm
is a basis of SU0 = <e1, ..., em>. Consequently, there exist z2, ..., zm  SU , such that zj(0) = zj0 for j = 2, ..., m. Then y, z2, ..., zm are linearly independent,
which implies that <y, z2, ..., zm> is an m-dimensional subspace of SU . Hence, there exist
y1, ..., ym
SU , such that zj(0) = zj0 for j = 2, ..., m. Then y, z2, ..., zm are linearly independent,
which implies that <y, z2, ..., zm> is an m-dimensional subspace of SU . Hence, there exist
y1, ..., ym  <y, z2, ..., zm>, such that yj(0) = ej for j = 1, ..., m and y
<y, z2, ..., zm>, such that yj(0) = ej for j = 1, ..., m and y  <y, z2, ..., zm> =
<y1, ..., ym> =: SU '.
<y, z2, ..., zm> =
<y1, ..., ym> =: SU '. ![[]](lasy10-c-32.gif)
Let N(SU ) denote the set 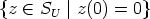 . Then N(SU ) is a subspace of SU . The
appearance of this subspace N(SU ) of SU , which is in general not
. Then N(SU ) is a subspace of SU . The
appearance of this subspace N(SU ) of SU , which is in general not 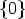 , is one of the main
differences to the case of mappings U: A
, is one of the main
differences to the case of mappings U: A  GL(n, K). We will see that N(SU ) is closely
related to the space W . This is described in
GL(n, K). We will see that N(SU ) is closely
related to the space W . This is described in
Lemma 18. A function z: A  Kn belongs to N(S
U ) if and only if
Kn belongs to N(S
U ) if and only if
 | (24) |
-
- Proof. The function z belongs to N(SU ) if and only if
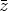 (0) = 0 and U11(
(0) = 0 and U11( +
+  )
)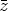 (
( ) =
U11(
) =
U11( )
)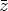 (
( +
+  ) for all
) for all  ,
,  ,
, 
 A. Especially for
A. Especially for  =
=  = 0 and because of the particular
form of U11 given in (20) we get
= 0 and because of the particular
form of U11 given in (20) we get
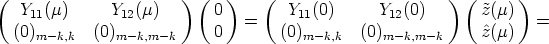
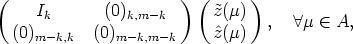
so that 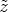 (
( ) = 0 for all
) = 0 for all 
 A. For
A. For  = 0 we derive
= 0 we derive
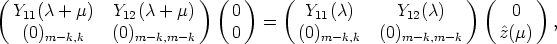
so that Y 12( )
)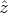 (
( ) = 0 for all
) = 0 for all  ,
, 
 A. This however implies that
A. This however implies that  (
( )
)  W for all
W for all

 A.
A.
Assuming conversely that 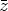 (0) = 0,
(0) = 0, 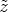 (
( ) = 0 and
) = 0 and 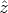 (
( )
)  W for all
W for all 
 A, then it is
obvious that z
A, then it is
obvious that z  N(SU ).
N(SU ). ![[]](lasy10-c-32.gif)
In conclusion we get the following result:
Lemma 19. Let SU ' be an m-dimensional subspace of S
U (constructed as above), then
SU = SU ' 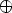 N(S
U ).
N(S
U ).
-
- Proof. It is clear that SU '
 N(S
U ) =
N(S
U ) =  and that SU '
and that SU '  N(S
U ) is a subspace of SU .
Assume that x is an element of SU , then there exists y
N(S
U ) is a subspace of SU .
Assume that x is an element of SU , then there exists y  SU ', such that y(0) = x(0).
Then z(
SU ', such that y(0) = x(0).
Then z( ) := x(
) := x( ) - y(
) - y( ) belongs to N(SU ). Hence x(
) belongs to N(SU ). Hence x( ) = z(
) = z( ) + y(
) + y( ), which finishes
the proof.
), which finishes
the proof. ![[]](lasy10-c-32.gif)
We notice that in the decomposition SU = SU '  N(S
U ) the space SU ' is in general not
uniquely determined, whereas N(SU ) is unique by definition. However, SU ' can be any
m-dimensional subspace of SU , such that the space of initial values y(0) (for y
N(S
U ) the space SU ' is in general not
uniquely determined, whereas N(SU ) is unique by definition. However, SU ' can be any
m-dimensional subspace of SU , such that the space of initial values y(0) (for y  SU ') is
already SU0.
SU ') is
already SU0.
As an immediate consequence we get
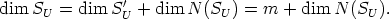
The following Theorem 20 yields together with Theorem 16 the structure of the space
SU , of all solutions of (2), for a given function U: A  Mn(K). These theorems
also contain necessary conditions on U in order to admit a nontrivial solution y.
Mn(K). These theorems
also contain necessary conditions on U in order to admit a nontrivial solution y.
We finish by Theorem 21, which provides a construction of all solutions (U, y) of (2) by
starting from an arbitrary subspace of initial values y(0) of Kn. This choice then leads via the
block matrix Y ( ) satisfying (19) to a matrix valued function U and a space S of solutions
corresponding to U. In this general situation we do not discuss the problem when S = SU .
) satisfying (19) to a matrix valued function U and a space S of solutions
corresponding to U. In this general situation we do not discuss the problem when S = SU .
-
- Proof. From the special form of U(
 ) and y(
) and y( ) it is clear that (2) is satisfied if and
only if U11(
) it is clear that (2) is satisfied if and
only if U11( +
+  )[
)[ (
( ) +
) +  (
( )] = U11(
)] = U11( )[
)[ (
( +
+  ) +
) + 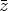 (
( +
+  )] for all
)] for all  ,
,  ,
, 
 A. This is
equivalent to U11(
A. This is
equivalent to U11( +
+  )[Y (
)[Y ( )
)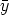 (0) +
(0) + 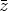 (
( )] = U11(
)] = U11( )[Y (
)[Y ( +
+  )
)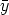 (0) +
(0) + 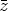 (
( +
+  )]. Due to the
definition of
)]. Due to the
definition of 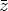 (
( ) this is equivalent to U11(0)[Y (
) this is equivalent to U11(0)[Y ( +
+  )Y (
)Y ( ) - Y (
) - Y ( )Y (
)Y ( +
+  )]
)]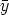 (0) = 0 for
all
(0) = 0 for
all  ,
,  ,
, 
 A. Since
A. Since 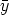 (0) is an arbitrary element of Km we derive
(0) is an arbitrary element of Km we derive
![U11(0)[Y (c + m)Y (n) - Y (c)Y(m + n)] = (0)m,m, A c, m,n (- A.](reich_son192x.gif)
We can rewrite U11(0)[Y ( +
+  )Y (
)Y ( ) - Y (
) - Y ( )Y (
)Y ( +
+  )] as U11(0)[Y (
)] as U11(0)[Y ( +
+  )Y (
)Y ( ) - Y (
) - Y ( +
+
 +
+  ) + Y (
) + Y ( +
+  +
+  ) - Y (
) - Y ( )Y (
)Y ( +
+  )] = U11(0)[Y (
)] = U11(0)[Y ( +
+  )Y (
)Y ( ) - Y (
) - Y ( +
+  +
+  )] +
U11(0)[Y (
)] +
U11(0)[Y ( +
+  +
+  ) - Y (
) - Y ( )Y (
)Y ( +
+  )], which is equal to (0)m,m since (19) holds.
)], which is equal to (0)m,m since (19) holds. ![[]](lasy10-c-32.gif)
In order to determine all solutions (U, y) of (2) we start with an arbitrary m-dimensional
subspace S0 of Kn for some 0 < m < n. Let 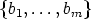 be a basis of S0, then there exists a
matrix B
be a basis of S0, then there exists a
matrix B  GL(n, K), such that Bbi = ei for 1 < i < m. Hence BS0 = <e
1, ..., em>. For each
solution Y (
GL(n, K), such that Bbi = ei for 1 < i < m. Hence BS0 = <e
1, ..., em>. For each
solution Y ( ) of (19) described in Theorem 16 let U11(
) of (19) described in Theorem 16 let U11( ) be given by (20) and U(
) be given by (20) and U( )
be given by (13) with arbitrary matrices U12(
)
be given by (13) with arbitrary matrices U12( ) and U22(
) and U22( ). Then each element y
of
). Then each element y
of
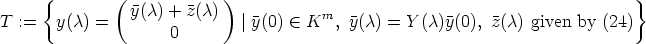
is together with U a solution of (2). Due to this construction T 0, the space of initial values
y(0) for y  T , is equal to <e1, ..., em>. According to Lemma 1 each pair (UB, B-1y) for y
T , is equal to <e1, ..., em>. According to Lemma 1 each pair (UB, B-1y) for y  T
is a solution of (2) and
T
is a solution of (2) and 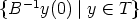 = S0. Hence, by varying S0 over all subspaces of
Kn we determine all solutions (U, y) of (2).
= S0. Hence, by varying S0 over all subspaces of
Kn we determine all solutions (U, y) of (2).
References
[1] H. Fripertinger and J. Schwaiger. Some applications of functional equations in
astronomy. Grazer Mathematische Berichte, 344 (2001), 1-6.
[2] R. Lidl and H. Niederreiter. Finite Fields, volume 20 of Encyclopedia of Mathematics
and its Applications. Addison-Wesley Publishing Company, London, Amsterdam,
Don Mills - Ontario, Sydney, Tokyo, 1983. ISBN 0-201-13519-1.
[3] M.A. McKiernan. The matrix equation a(xoy) = a(x)+a(x)a(y)+a(y). Aequationes
Mathematicae, 15 (1977), 213-223.
[4] J. Schwaiger. Some applications of functional equations in astronomy. Aequationes
Mathematicae, 60 (2000), p. 185. In Report of the meeting, The Thirty-seventh
International Symposium on Functional Equations, May 16-23, 1999, Huntington,
WV.
HARALD FRIPERTINGER
LUDWIG REICH
Institut für Mathematik
Karl-Franzens-Universität Graz
Heinrichstr. 36/4
A-8010 Graz
Austria
harald.fripertinger@kfunigraz.ac.at
ludwig.reich@kfunigraz.ac.at
|
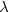 +
+ 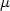 )y(
)y( ) = U(
) = U(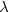 )y(
)y(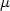 +
+  ) (
) (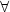
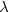 ,
, 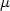 ,
, 
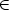 A) of the functional
equation of the mean sun are studied, where (A, +) is an Abelian group, K
is a field, n is a positive integer, and both y: A
A) of the functional
equation of the mean sun are studied, where (A, +) is an Abelian group, K
is a field, n is a positive integer, and both y: A  Kn and U: A
Kn and U: A  GL(n, k)
(or U: A
GL(n, k)
(or U: A  Mn(k) in the second case) are unknown functions, which will be
determined by the equation.
Mn(k) in the second case) are unknown functions, which will be
determined by the equation.
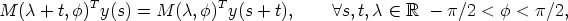
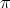
 ,
, 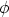
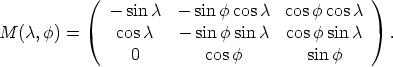
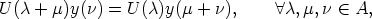

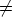 0) exists. A similar
description of
0) exists. A similar
description of 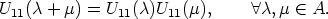

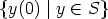 is a given subspace
is a given subspace 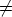 0 (cf. Lemma
0 (cf. Lemma 

![[]](lasy10-c-32.gif)
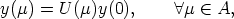
![[U (c + m) - U (c)U (m)]y(0) = 0, A c, m (- A.](reich_son8x.gif)

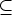
 .
Let
.
Let 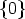 , then it follows from the second item of
this lemma that
, then it follows from the second item of
this lemma that 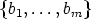 denotes a basis of
denotes a basis of 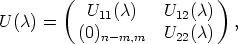
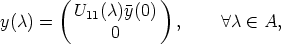
 (0)
(0) 
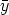 (
(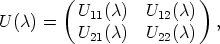
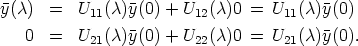
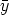 (0) is an arbitrary element of
(0) is an arbitrary element of 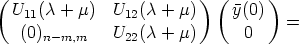
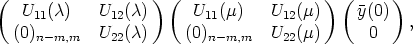
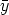 (0) =
(0) = 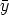 (0) for all
(0) for all 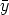 (0)
(0) 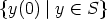
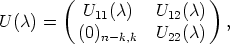
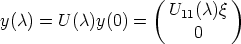
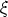
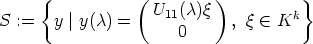
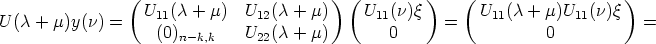
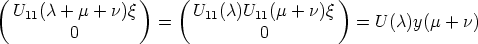

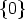
![( )
[U11(c0)U12(m0) + U12(c0)U22(m0) - U12(c0 + m0)]j /= 0.
[U22(c0)U22(m0) - U22(c0 + m0)]j](reich_son34x.gif)
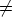 0. When writing
0. When writing 
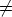 0. Together with (6) we get
0. Together with (6) we get
![( )
0 [U11(c)U12(m) + U12(c)U22(m) - U12(c + m)]j
[U (c + m) - U (c)U (m)]y = [U22(c)U22(m) - U22(c + m)]j ,](reich_son38x.gif)
![{j (- Kn -k |[U22(c)U22(m) - U22(c + m)]j = 0, A c,m (- A} .](reich_son39x.gif)
![A j (- Ks \{0} E c ,m (- K : [U (c )U (m ) - U (c + m )]j /= 0.
0 0 22 0 22 0 22 0 0](reich_son40x.gif)
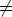 2
2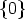 with
with 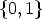 . Then
. Then 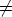
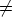 0
for all
0
for all 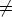 0.
0.
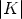
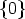 , such that
, such that 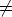 1. Let
1. Let 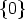 , then for
, then for 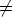 0 for all
0 for all 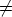 0.
0.
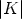 = 2
= 2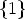 is a homomorphism,
so (8) cannot be satisfied. If
is a homomorphism,
so (8) cannot be satisfied. If 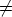 0 for all
0 for all
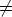 0, since 2
0, since 2 ![A j (- Kn -k\{0} E c0,m0 (- K : [U11(c0)U12(m0) + U12(c0)U22(m0) - U12(c0 + m0)]j /= 0.](reich_son57x.gif)
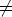 2
2
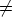 0 for all
0 for all 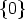 .
.
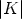
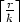 + 1
+ 1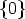 , then
, then 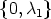 . Let
. Let
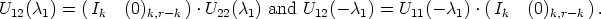
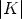 is big enough, then there exists
is big enough, then there exists 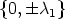 and we assume
that
and we assume
that
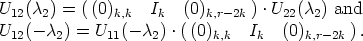
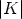 is big enough, then there exists
is big enough, then there exists 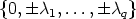 and
we assume that
and
we assume that
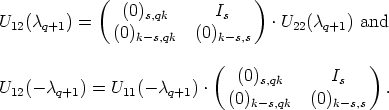
 , then there exists 1
, then there exists 1  0. Hence, there
exists
0. Hence, there
exists 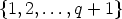 , such that (
, such that (
 + 1, but it is also possible to find
+ 1, but it is also possible to find 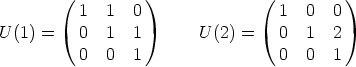
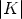
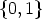 and then
and then
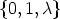 . Let furthermore
. Let furthermore 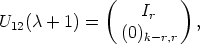
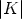
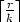 + 2
+ 2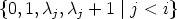 , such that
, such that 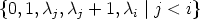 . Let
. Let
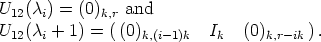
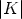 is big enough, then there exists
is big enough, then there exists 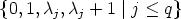 and we assume that
and we assume that
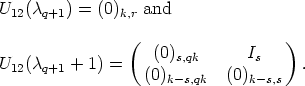
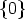 there exists 1
there exists 1  0. Hence, there exists
0. Hence, there exists
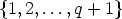 , such that (
, such that ( = 2
= 2
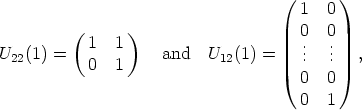
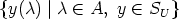 (cf. Lemma
(cf. Lemma 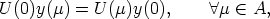
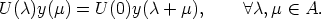
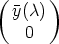
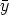 (
(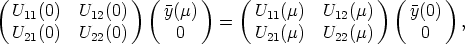
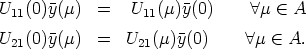
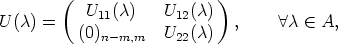
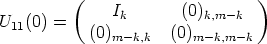
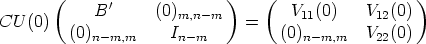
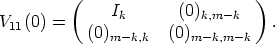
 (
(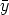 (0) for all
(0) for all 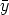 (0) can arbitrarily be chosen in
(0) can arbitrarily be chosen in 
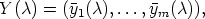
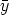
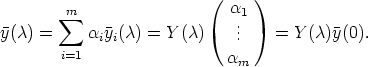
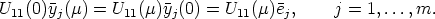
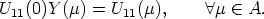
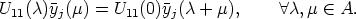
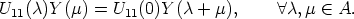
![U11(0)[Y (c + m)- Y (c)Y (m)] = (0)m,m, A c,m (- A.](reich_son118x.gif)
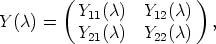
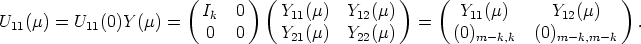
![( )[( ) ( )( )]
Ik 0 Y11(c + m) Y12(c + m) - Y11(c) Y12(c) Y11(m) Y12(m) = (0)
0 0 Y21(c + m) Y22(c + m) Y21(c) Y22(c) Y21(m) Y22(m) m,m](reich_son121x.gif)
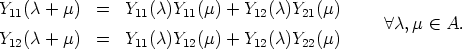
![Y12(c)[Y21(m1 + m2) - Y21(m1)Y11(m2) - Y22(m1)Y21(m2)] = 0, A c, m1,m2 (- A.](reich_son123x.gif)
![Y12(c)[Y22(m1 + m2) - Y21(m1)Y12(m2) - Y22(m1)Y22(m2)] = 0, A c, m1,m2 (- A.](reich_son124x.gif)



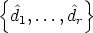 .
Moreover, there exists an
.
Moreover, there exists an 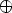
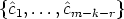 be a basis of
be a basis of 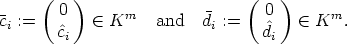
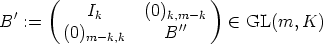
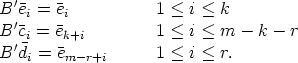
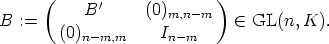
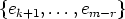 and
and 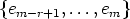 are a basis of
are a basis of 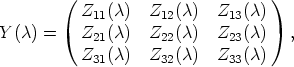
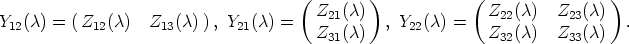
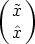
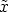
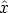
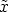 = 0. Moreover
= 0. Moreover 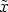 = 0 for all
= 0 for all 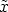 = 0.
= 0.
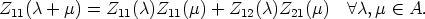
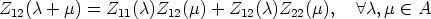
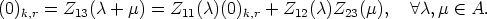
![Z12(c)[Z21(m1 + m2) - Z21(m1)Z11(m2) - Z22(m1)Z21(m2)] = (0)k,k, A c,m1, m2 (- A.](reich_son144x.gif)
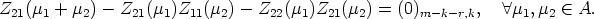
![Z12(c)[Z22(m1 + m2) - Z21(m1)Z12(m2) - Z22(m1)Z22(m2)] = (0)k,m -k-r, A c, m1,m2 (- A](reich_son146x.gif)
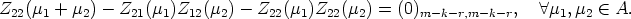
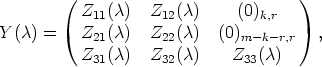
 0
0  0
0  0 also
0 also 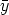 (0)
(0)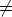 0. Hence there exist
0. Hence there exist 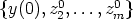 is a basis of
is a basis of 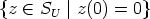 . Then
. Then 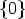 , is one of the main
differences to the case of mappings
, is one of the main
differences to the case of mappings 
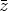 (0) = 0 and
(0) = 0 and 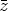 (
(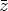 (
(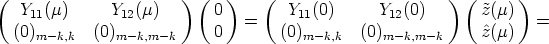
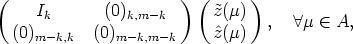
 (
(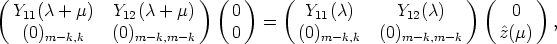
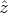 (
( (
(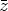 (0) = 0,
(0) = 0, 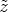 (
(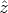 (
(
 and that
and that 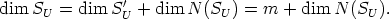
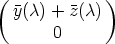

 (0)
(0)  (
(
 (0)
(0)  (
(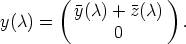
 (
( (
( (
(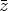 (
(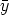 (0) +
(0) + 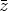 (
(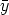 (0) +
(0) + 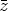 (
(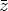 (
(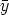 (0) = 0 for
all
(0) = 0 for
all 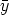 (0) is an arbitrary element of
(0) is an arbitrary element of ![U11(0)[Y (c + m)Y (n) - Y (c)Y(m + n)] = (0)m,m, A c, m,n (- A.](reich_son192x.gif)
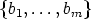 be a basis of
be a basis of 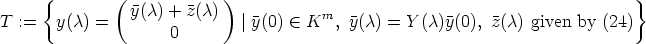
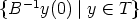 =
=