 3 and think the origin to be positioned at the center of the earth. Then, choosing the
initial time and the length of a (mean) solar day appropriately, the law of motion of the mean
sun is given by
3 and think the origin to be positioned at the center of the earth. Then, choosing the
initial time and the length of a (mean) solar day appropriately, the law of motion of the mean
sun is given by Local solar time is measured by a sundial. When the center of the sun is on an observer’s meridian, the observer’s local solar time is zero hours (noon). Because the earth moves with varying speed in its orbit at different times of the year and because the plane of the earth’s equator is inclined to its orbital plane, the length of the solar day is different depending on the time of year. It is more convenient to define time in terms of the average of local solar time. Such time, called mean solar time, may be thought of as being measured relative to an imaginary sun (the mean sun) that lies in the earth’s equatorial plane and about which the earth orbits with constant speed. Every mean solar day is of the same length.1
In mathematical terms this means the following: Let e = (e1, e2, e3) be the canonical base
of  3 and think the origin to be positioned at the center of the earth. Then, choosing the
initial time and the length of a (mean) solar day appropriately, the law of motion of the mean
sun is given by
3 and think the origin to be positioned at the center of the earth. Then, choosing the
initial time and the length of a (mean) solar day appropriately, the law of motion of the mean
sun is given by
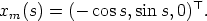 | (1) |
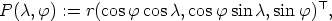
 the geographical
longitude and
the geographical
longitude and  the latitude of that point). Then the local coordinate frame is given by the
unit vectors indicating the directions East, North, and to the zenith. The transformation
matrix transforming the canonical base e to the local system, denoted by e(
the latitude of that point). Then the local coordinate frame is given by the
unit vectors indicating the directions East, North, and to the zenith. The transformation
matrix transforming the canonical base e to the local system, denoted by e( ,
,  ) is given by
) is given by
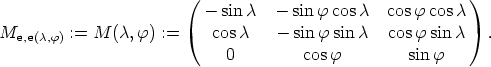 | (2) |
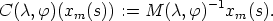
 ,
,  ), if the zenith component of C(
), if the zenith component of C( ,
,  )(xm(s)) is
maximal.
)(xm(s)) is
maximal.
Local Mean time (or local civil time) has the convenient property, that,
if it is noon at Greenwich, it is 1 p.m. at a position 15o east of Greenwich, or more general:
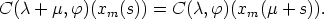
Thus xm satisfies the functional equation
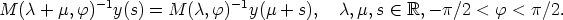 | (3) |
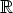

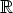 3 be given such that y(s) /= 0 for all real s and such that (3) holds
for all
3 be given such that y(s) /= 0 for all real s and such that (3) holds
for all  ,
, 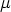 , s
, s 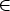
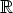 and some
and some 
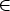 ] -
] - 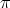 /2,
/2, 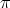 /2[. Let furthermore
/2[. Let furthermore
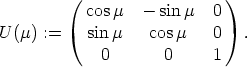 | (4) |
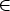
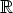 3, c /= 0, such that
3, c /= 0, such that
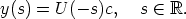 | (5) |
![[]](lasy10-c-32.gif)
Now we come to a problem for which it is important to take the earth’s radius into account.
Satellite dishes point to positions given by geostationary satellites, and thus have the desired
property of fixed positions invariant with respect to time. Thus, if y(s) is the position of the
satellite at time s, the property required is that the direction vector belonging to 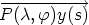 ,
i.e., the unit vector corresponding to this vector, expressed in local coordinates be independent
of s:
,
i.e., the unit vector corresponding to this vector, expressed in local coordinates be independent
of s:
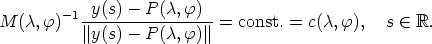 | (6) |
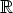

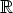 3,
3, 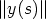 /= 1 for all s
/= 1 for all s 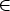
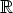 , the expression
, the expression
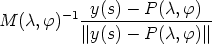
 i,
i, 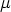 i), i = 1, 2, 3, then y itself
is constant. Moreover every constant vector of length different from 1 satisfies (6).
i), i = 1, 2, 3, then y itself
is constant. Moreover every constant vector of length different from 1 satisfies (6).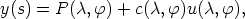
 ,
,  ). Thus
). Thus
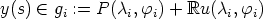
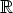 3.
3.
If, say, u( i,
i,  i) and u(
i) and u( j,
j,  j) are linearly independent, the intersection of gi and gj
contains at most one point. Since y(s)
j) are linearly independent, the intersection of gi and gj
contains at most one point. Since y(s) 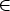 gi
gi  gj this implies that y(s) equals the point
of intersection of those two lines for all s. Thus y has to be constant.
gj this implies that y(s) equals the point
of intersection of those two lines for all s. Thus y has to be constant.
The (only) other possibility left means that the two vectors u( 1,
1,  1), u(
1), u( 2,
2,  2) as
well as the vectors u(
2) as
well as the vectors u( 1,
1,  1) and u(
1) and u( 3,
3,  3) are linearly dependent. But then all three lines
g1, g2, g3 coincide, since they have a point in common and since they have proportional
direction vectors. Thus the three different points P (
3) are linearly dependent. But then all three lines
g1, g2, g3 coincide, since they have a point in common and since they have proportional
direction vectors. Thus the three different points P ( 1,
1,  1), P (
1), P ( 2,
2,  2), P (
2), P ( 3,
3,  3) of the
same length are collinear, which is impossible.
3) of the
same length are collinear, which is impossible. ![[]](lasy10-c-32.gif)
Now, as we have been successful with taking into account the radius of the earth in solving
this problem, we want to reconsider, in the same spirit, the original problem. We again
suppose this radius r to be of length 1 and we suppose for y that 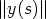 /= 0 for all s. The
functional equation then reads as
/= 0 for all s. The
functional equation then reads as
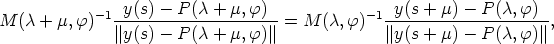 | (7) |
 ,
, 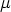 , s
, s 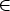
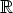 and all -
and all -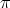 /2 <
/2 <  <
< 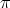 /2.
/2.
 ,
, 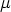 , s
, s 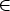
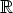 and some -
and some -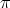 /2 <
/2 <  <
< 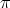 /2,
where y :
/2,
where y : 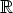

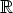 3 is such, that
3 is such, that 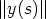 /= 1 for all s. Then there is some constant vector
c
/= 1 for all s. Then there is some constant vector
c 
 3,
3,  /= 1, such that
/= 1, such that
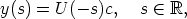
 ,
, 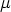 , s
, s 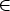
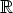 and all -
and all -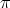 /2 <
/2 <  <
< 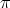 /2.
/2.
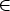 ] -
] - 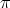 /2,
/2, 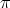 /2[ we put c(s,
/2[ we put c(s,  ) :=
) := 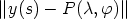 and
u(s,
and
u(s,  ) :=
) := 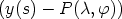 /c(s,
/c(s,  ). This means
). This means
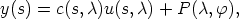 | (8) |
 ) > 0 and u(s,
) > 0 and u(s,  ) is a unit vector. Then (7) and the relation at the beginning of
the proof of the first theorem imply
) is a unit vector. Then (7) and the relation at the beginning of
the proof of the first theorem imply
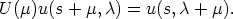 | (9) |
 = 0 gives
= 0 gives
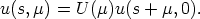 | (10) |
 ,
,  ) = U(
) = U( )P (0,
)P (0,  ) and U(
) and U( +
+ 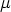 ) = U(
) = U( )U(
)U(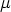 ). Thus (8) reads as
). Thus (8) reads as
![y(s) = U (c)[P (0,f) + c(s,c)u(s + c,0)]](meansun27x.gif) | (11) |
 = 0
= 0
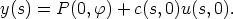 | (12) |

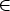
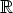 we consider the straight line
we consider the straight line 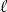
 determined by y(0) and P (
determined by y(0) and P ( ,
,  ).
).
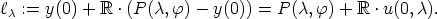
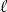
 may contain at most two unit vectors, one of them being P (
may contain at most two unit vectors, one of them being P ( ,
,  ).
).
Thus for any fixed real t there is some  such that P (
such that P ( ,
,  )
)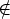
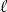 t. Then obviously
y(0)
t. Then obviously
y(0) 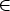
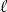

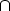
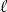 t; and it is the only point in that intersection of the two lines
t; and it is the only point in that intersection of the two lines 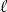
 and
and 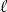 t, since
P (
t, since
P ( ,
,  )
)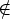
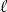 t:
t:
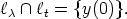 | (13) |
 replaced by
replaced by  - t and s replaced by t
- t and s replaced by t
![y(t) = P (c - t,f) + c(t,c - t)u(t,c - t) (-
(- U (- t)[P (c,f) + RU (t)u(t,c - t)] =
= U (- t)[P (c,f) + Ru(0, c)] = U(- t)lc,](meansun33x.gif)
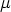 replaced by t, s by 0 and
replaced by t, s by 0 and  by
by  - t. We also have
- t. We also have
![y(t) (- P (0,f) + R (y(t)- P(0,f)) = P(0,f) + Ru(t, 0) =
= U (- t)[U(t)[P (0, f) + Ru(t,0)]] = U(- t)[P(t,f) + RU (t)u(t,0)] =
= U (- t)lt,](meansun34x.gif)
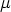 = t.
= t.
Thus
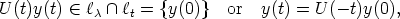
![[]](lasy10-c-32.gif)
[1] Blatter, Ch., Von den Keplerschen Gesetzen zu einer minutengenauen Sonnenuhr (From Kepler’s laws to a minute-exact sundial). Elem. Math. 49, No.4(1994), 155-165.
[2] Fripertinger, H., The functional equation of the mean sun written as a group action. Grazer Math. Ber. ....
[2] Fripertinger, H. and Reich, L., Generalizations of the functional equation of the mean sun. Grazer Math. Ber. ....
[4] Schwaiger, J., Die Ringsonnenuhr -- eine mathematische Analyse. To appear in Mitt. Math. Ges. Hamburg.
Harald Fripertinger
|