Enumeration of non-isomorphic canons
Harald Fripertinger
|
Abstract
In this note we describe how to apply group actions in order to enumerate the
isomorphism classes of rhythmic canons.
|
The notion of a rhythmic canon was originally formalized by O. Messiaen. He proposed to
study canonical musical forms in which the imitation between the different voices concerns
only rhythmical aspects, independent from melody or harmony. The first mathematical
investigation of rhythmic canons goes back to Vuza’s papers [7, 9, 8, 10] in which he actually
introduced even much more complicated families of canons, the “Regular Complementary
Canons of Maximal Category” (in short RCMC-canons). Their definition will be given
below.
Before describing rhythmic canons in cyclic time, we view them as they may appear within
a musical composition, in free linear time which has no cyclicity. Like in a melodic canon, one
has several voices that may enter one after the other until all voices are present. As in the
case of a melodic canon, all voices are just copies of a ground voice that is suitably
translated in the time axis. For simplicity we suppose here that all voices are extended in
both directions of the time axis ad infinitum. We further suppose that the ground
voice is a periodic rhythm that we will call the inner rhythm. Following Vuza’s
definition, a periodic rhythm is an infinite subset R of the rationals 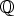 (marking the
attack times, or onsets) with R = R + d for a suitable period d. Furthermore, R is
supposed to be locally finite (i.e. the intersection of R with every time segment
[a, b] (of finite length b - a > 0) is finite). The period of a periodic rhythm R is the
smallest positive rational number d = d(R) satisfying R = R + d. We also mention
another important characteristic of a periodic rhythm, its pulsation p = p(R). It is
defined as the max
(marking the
attack times, or onsets) with R = R + d for a suitable period d. Furthermore, R is
supposed to be locally finite (i.e. the intersection of R with every time segment
[a, b] (of finite length b - a > 0) is finite). The period of a periodic rhythm R is the
smallest positive rational number d = d(R) satisfying R = R + d. We also mention
another important characteristic of a periodic rhythm, its pulsation p = p(R). It is
defined as the max 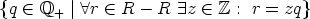 , in other words, it is
the biggest rational q such that all distances between the attack points of R are
integer multiples of q. Obviously, the period d is an integer multiple of the pulsation
p.
, in other words, it is
the biggest rational q such that all distances between the attack points of R are
integer multiples of q. Obviously, the period d is an integer multiple of the pulsation
p.
Let A be the set of all rational numbers a such that the attack times of the voices of the
canon can be expressed as R + a. Then A itself is a periodic rhythm, called the outer rhythm
of the canon, with period d(A), where d(R) is an integer multiple of d(A). Note that R and A
may have different pulsations p(R) and p(A). Hence, the pulsation of a canon is defined as the
greatest rational number p such that both p(R) and p(A) are integer multiples of
p.
In order to switch from linear time to circular time the fraction n = d(R)/p must be
computed. Let r denote a fixed attack time within the inner rhythm R. Then each attack time
in any of the voices is of the form r + tp for a suitable integer t, i.e. the whole canon is
contained in r + p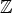
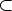
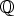 . Because everything is periodic with period d(R), we can restrict to
the factor space (r + p
. Because everything is periodic with period d(R), we can restrict to
the factor space (r + p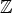 )/d(R)
)/d(R)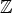 which may be identified with
which may be identified with 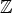 /n
/n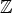 , the residue class ring of
, the residue class ring of
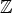 modulo n
modulo n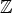 .
.
From now on, we consider the whole canon within Zn := 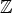 /n
/n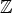 and assume that R, A, and
V a denote the projections of the inner rhythm, the outer rhythm, and the voices of a
canon.
and assume that R, A, and
V a denote the projections of the inner rhythm, the outer rhythm, and the voices of a
canon.
The concept of a canon used in the present paper is described by G. Mazzola in [4] and was
presented by him to the author in the following way: A canon is a subset K 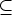 Zn together
with a covering of K by pairwise different subsets, the voices, V i
Zn together
with a covering of K by pairwise different subsets, the voices, V i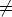 Ø for 1 < i < t, where t > 1
is the number of voices of the canon,
Ø for 1 < i < t, where t > 1
is the number of voices of the canon,
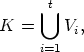
such that for all i, j 
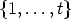
- the set V i can be obtained from V j by a translation of Zn,
- there is only the identity translation which maps V i to V i,
- the set of differences in K generates Zn, i.e. <K - K> := <k - l | k, l
 K> = Zn.
K> = Zn.
We prefer to write a canon K as a set of its subsets V i. Two canons K = 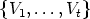 and
L =
and
L = 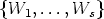 are called isomorphic if s = t and if there exists a translation T of Zn and
a permutation
are called isomorphic if s = t and if there exists a translation T of Zn and
a permutation 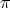 in the symmetric group St such that T (V i) = W
in the symmetric group St such that T (V i) = W  (i) for 1 < i < t. Then
obviously T (K) = L.
(i) for 1 < i < t. Then
obviously T (K) = L.
The aim of this note is to determine the number of non-isomorphic canons for
given n. First we present the definition of canons in more details and give a short
description of group actions, which are the standard tool to describe isomorphism
classes of different objects (cf.[2, 3]). Since we are interested in the attack times
modulo n, we assume that K is a subset of Zn. The set of translations of Zn is the
cyclic group Cn generated by the permutation  n := (0, 1, ..., n - 1) which maps i to
i + 1 mod n. Cn acts in a natural way both on Zn and on the set of all subsets of
Zn:
n := (0, 1, ..., n - 1) which maps i to
i + 1 mod n. Cn acts in a natural way both on Zn and on the set of all subsets of
Zn:
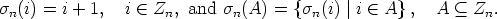
As usual we identify a subset A of Zn with its characteristic function 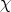 A : Zn
A : Zn 
 given
by
given
by
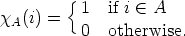
The set of all functions from a set X to a set Y will be indicated as Y X. For arbitrary
f 
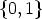 Zn let
Zn let 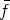 denote the subset f-1(
denote the subset f-1(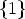 ) of Z
n, whence f =
) of Z
n, whence f = 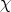
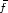 .
.
Sometimes it is convenient to write functions f from Zn to 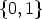 as vectors of
the form (f(0), f(1), ..., f(n - 1)) using the natural order of the elements of Zn,
because then the set of all these functions is totally ordered by the lexicographic
order. For functions f, g
as vectors of
the form (f(0), f(1), ..., f(n - 1)) using the natural order of the elements of Zn,
because then the set of all these functions is totally ordered by the lexicographic
order. For functions f, g 
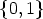 Zn we say f < g if there exists an i
Zn we say f < g if there exists an i  Z
n such that
f(j) = g(j) for 0 < j < i and f(i) < g(i). The group action of Cn on the set of all
subsets of Zn described as an action on the set of all characteristic function is the
following
Z
n such that
f(j) = g(j) for 0 < j < i and f(i) < g(i). The group action of Cn on the set of all
subsets of Zn described as an action on the set of all characteristic function is the
following
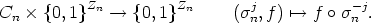
As the canonical representative of the orbit Cn(f) = 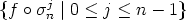 we choose the
function f0
we choose the
function f0  Cn(f) such that f0 < g for all g
Cn(f) such that f0 < g for all g  Cn(f). Moreover, we choose
Cn(f). Moreover, we choose 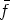 0 as the
canonical representative of the orbit Cn(
0 as the
canonical representative of the orbit Cn(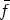 ) =
) =  . In general,
representatives of orbits Cn(f) of functions f under the action of the cyclic group Cn are
called necklaces.
. In general,
representatives of orbits Cn(f) of functions f under the action of the cyclic group Cn are
called necklaces.
-
- Lemma 1. If f
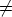 0 denotes a function from Zn to
0 denotes a function from Zn to 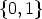 , then the canonical
representative f0 of the orbit Cn(f) fulfills f0(n - 1) = 1.
, then the canonical
representative f0 of the orbit Cn(f) fulfills f0(n - 1) = 1.
A function f 
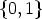 Zn (or the corresponding vector and the set
Zn (or the corresponding vector and the set  ) is called acyclic if C
n(f)
consists of n different objects. The canonical representative of the orbit of an acyclic function
is usually called a Lyndon word. If f is acyclic, then all elements in the orbit Cn(f) are acyclic
as well, and we call Cn(f) an acyclic orbit.
) is called acyclic if C
n(f)
consists of n different objects. The canonical representative of the orbit of an acyclic function
is usually called a Lyndon word. If f is acyclic, then all elements in the orbit Cn(f) are acyclic
as well, and we call Cn(f) an acyclic orbit.
From the first two properties of a canon we derive that all voices V i belong to the same
orbit Cn(V 1) and that each voice is acyclic. For that reason, we can describe a canon
K = 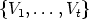 as a pair (L, A) where L is the Lyndon word, which is the canonical
representative of the orbit Cn(
as a pair (L, A) where L is the Lyndon word, which is the canonical
representative of the orbit Cn(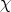 V 1), and A =
V 1), and A = 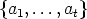 is a t-subset of Zn such that
V i =
is a t-subset of Zn such that
V i =  nai(L). In other words, L describes the inner rhythm and A the outer rhythm of
K.
nai(L). In other words, L describes the inner rhythm and A the outer rhythm of
K.
Now we analyse in which situations a pair (L, A), as described above, is not a canon, i.e.
when it fails to fulfill the third property. Assume that (L, A) is not a canon, then the
differences K - K generate a proper subgroup of Zn. This subgroup is isomorphic to Zn/d
where d > 1 is a divisor of n. In other words, d is a divisor of all differences k - l for all
k, l  K. We write d | r in order to express that the integer d is a divisor of the
integer r. (It is not connected with division in the ring Zn.) It is easy to prove the
following
K. We write d | r in order to express that the integer d is a divisor of the
integer r. (It is not connected with division in the ring Zn.) It is easy to prove the
following
-
- Lemma 2. Let L
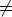 0 be a Lyndon word of length n, and let A be a t-subset of Zn. The
pair (L, A) does not describe a canon in Zn if and only if there exists an integer d > 1
such that d | n, d | k - l for all k, l
0 be a Lyndon word of length n, and let A be a t-subset of Zn. The
pair (L, A) does not describe a canon in Zn if and only if there exists an integer d > 1
such that d | n, d | k - l for all k, l 
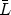 , and d | k - l for all k, l
, and d | k - l for all k, l  A.
A.
Consider the set S of all pairs (L, A) where L is a Lyndon word and A is a t-subset of Zn. The
group of translations of Zn acts on S according to
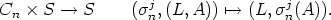
If (L, A) is a canon, then the orbit Cn(L, A) = (L, Cn(A)) describes the isomorphism class of
(L, A). In general, the canonical representative of Cn(L, A) is (L, A0) where A0 is the
canonical representative of Cn(A). From Lemma 1 we already know that 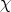 A0(n - 1) = 1 and
L(n - 1) = 1 if L
A0(n - 1) = 1 and
L(n - 1) = 1 if L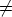 0. This together with Lemma 2 proves
0. This together with Lemma 2 proves
-
- Lemma 3. Let L
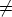 0 be a Lyndon word of length n, and let A be a t-subset of Zn. The
pair (L, A) does not describe a canon in Zn if and only if there exists a divisor d > 1 of
n such that L(i) = 1 implies i
0 be a Lyndon word of length n, and let A be a t-subset of Zn. The
pair (L, A) does not describe a canon in Zn if and only if there exists a divisor d > 1 of
n such that L(i) = 1 implies i  d - 1 mod d, and
d - 1 mod d, and 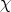 A0(i) = 1 implies i
A0(i) = 1 implies i  d - 1 mod d,
where A0 is the canonical representative of Cn(A).
d - 1 mod d,
where A0 is the canonical representative of Cn(A).
In the next part we show that functions f 
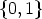 Zn with the property f(i) = 1 implies
i
Zn with the property f(i) = 1 implies
i  -1 mod d (for d | n, d > 1) can be constructed from functions in
-1 mod d (for d | n, d > 1) can be constructed from functions in 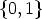 Zn/d
. Let
Zn/d
. Let  d be a
function defined on
d be a
function defined on 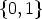 , such that
, such that  d(0) is the vector (0, 0, ..., 0) consisting of d entries of 0,
and
d(0) is the vector (0, 0, ..., 0) consisting of d entries of 0,
and  d(1) = (0, ..., 0, 1) is a vector consisting of d - 1 entries of 0 and 1 in the last position.
We write the values of
d(1) = (0, ..., 0, 1) is a vector consisting of d - 1 entries of 0 and 1 in the last position.
We write the values of  d in the form
d in the form
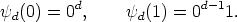
If we apply  d to each component of a vector f
d to each component of a vector f 
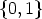 Zr by replacing each component
0 in f by 0d and each component 1 by 0d-11, we get a vector
Zr by replacing each component
0 in f by 0d and each component 1 by 0d-11, we get a vector  d(f)
d(f) 
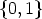 Zrd
and
Zrd
and
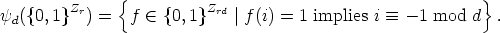
From Lemma 3 we conclude that (L, A) does not describe a canon if and only if there exists a
d > 1 which divides n such that both L and 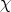 A0 are elements of
A0 are elements of  d(
d(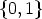 Zn/d
).
Zn/d
).
Some properties of  d are collected in the next
d are collected in the next
-
- Lemma 4. Let f, g be functions from Zr to
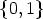 . Then
. Then
 d(f) =
d(f) =  d(g) if and only if f = g.
d(g) if and only if f = g.
 d(f o
d(f o  r) =
r) =  d(f) o
d(f) o  rdd.
rdd.
 d(Cr(f))
d(Cr(f)) 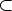 Crd(
Crd( d(f)).
d(f)).
- f < g if and only if
 d(f) <
d(f) <  d(g).
d(g).
- f0 is the canonical representative of Cr(f) if and only if
 d(f0) is the canonical
representative of Crd(
d(f0) is the canonical
representative of Crd( d(f)).
d(f)).
 d describes a bijection between the Cr-orbits on
d describes a bijection between the Cr-orbits on 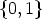 Zr and the C
rd-orbits on
Zr and the C
rd-orbits on
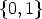 Zrd which have non-empty intersection with
Zrd which have non-empty intersection with  d(
d(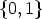 Zr), thus
Zr), thus
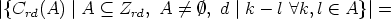
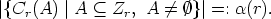
- f
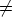 0 is acyclic if and only if
0 is acyclic if and only if  d(f) is acyclic.
d(f) is acyclic.
 d describes a bijection between the acyclic Cr-orbits on
d describes a bijection between the acyclic Cr-orbits on 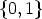 Zr and the acyclic
Crd-orbits on
Zr and the acyclic
Crd-orbits on 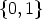 Zrd which have non-empty intersection with
Zrd which have non-empty intersection with  d(
d(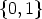 Zr), thus
Zr), thus
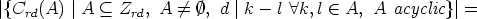
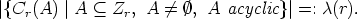
- Both f and
 d(f) have the same number of components which are 1.
d(f) have the same number of components which are 1.
-
- Proof. Since
 d is an injective mapping from each component of f into the set
d is an injective mapping from each component of f into the set
 , the first statement is clear.
, the first statement is clear.
In order to show that the second item is true, assume that  d(f o
d(f o  r)(j) = 1 for
some j
r)(j) = 1 for
some j  Zrd. According to the definition of
Zrd. According to the definition of  d, this is equivalent to j = sd - 1 and
(f o
d, this is equivalent to j = sd - 1 and
(f o  r)(s - 1) = 1 for some s
r)(s - 1) = 1 for some s 
 . In other words, j = sd - 1 and f(s) = 1,
which is equivalent to j = sd - 1 and
. In other words, j = sd - 1 and f(s) = 1,
which is equivalent to j = sd - 1 and  d(f)((s + 1)d - 1) = 1. This, however, is the same
as
d(f)((s + 1)d - 1) = 1. This, however, is the same
as  d(f)(j + d) = 1, whence (
d(f)(j + d) = 1, whence ( d(f) o
d(f) o  rdd)(j) = 1. If f = 0 the assertion is always true.
rdd)(j) = 1. If f = 0 the assertion is always true.
The third part is an immediate consequence of the second.
If f < g, then there exists i  Zr such that f(j) = g(j) for all j < i and f(i) < g(i),
whence f(i) = 0 and g(i) = 1. For that reason,
Zr such that f(j) = g(j) for all j < i and f(i) < g(i),
whence f(i) = 0 and g(i) = 1. For that reason,  d(f(i)) = 0d and
d(f(i)) = 0d and  d(g(i)) = 0d-11.
Hence,
d(g(i)) = 0d-11.
Hence,  d(f)(j) =
d(f)(j) =  d(g)(j) for j < id-1 and
d(g)(j) for j < id-1 and  d(f)(id-1) = 0 < 1 =
d(f)(id-1) = 0 < 1 =  d(g)(id-1), and
consequently
d(g)(id-1), and
consequently  d(f) <
d(f) <  d(g). If, conversely,
d(g). If, conversely,  d(f) <
d(f) <  d(g), then there exists an i
d(g), then there exists an i  Zrd
such that
Zrd
such that  d(f)(j) =
d(f)(j) =  d(g)(j) for all j < i and
d(g)(j) for all j < i and  d(f)(i) <
d(f)(i) <  d(g)(i), whence
d(g)(i), whence  d(g)(i) = 1
and i
d(g)(i) = 1
and i  -1 mod d. Assume that i is of the form sd - 1. Then
-1 mod d. Assume that i is of the form sd - 1. Then  d(f(j)) =
d(f(j)) =  d(g(j)) for
j < s, and
d(g(j)) for
j < s, and  d(f(s)) = 0d whereas
d(f(s)) = 0d whereas  d(g(s)) = 0d-11. Since
d(g(s)) = 0d-11. Since  d is an injective mapping,
f(j) = g(j) for j < s and f(s) = 0 < 1 = g(s), which implies that f < g.
d is an injective mapping,
f(j) = g(j) for j < s and f(s) = 0 < 1 = g(s), which implies that f < g.
From the definition of the canonical representative of an orbit and from the items
4. and 2. it follows immediately that  d(f0) <
d(f0) <  d(f0 o
d(f0 o  rj) =
rj) =  d(f0) o
d(f0) o  rddj for
all j
rddj for
all j 
 . Moreover, if n /
. Moreover, if n / 0 mod d, then (
0 mod d, then ( d(f0) o
d(f0) o  rdn)(rd - 1) =
rdn)(rd - 1) =
 d(f0)(n - 1)
d(f0)(n - 1) 1, since n - 1 /
1, since n - 1 / -1 mod d. According to Lemma 2, the representative
-1 mod d. According to Lemma 2, the representative
 d(f0) o
d(f0) o  rdn cannot be the canonical representative of the orbit Crd(
rdn cannot be the canonical representative of the orbit Crd( d(f0)). Hence,
the canonical representative is
d(f0)). Hence,
the canonical representative is  d(f0).
d(f0).
Then 6. is a trivial consequence of 5. Similar arguments can be applied for proving
7. and 9. Item 8. follows immediately from 7. ![[]](lasy10-c-32.gif)
In order to compute the number of all Cr-orbits on  Zr we apply Pólya’s theory
cf. [2, 3, 5, 6]. In the present situation we have to compute the cycle index of the group Cr acting
on Zr which is a polynomial in z1, ..., zr over
Zr we apply Pólya’s theory
cf. [2, 3, 5, 6]. In the present situation we have to compute the cycle index of the group Cr acting
on Zr which is a polynomial in z1, ..., zr over 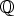 given by
given by
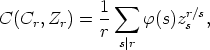
where 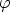 is the Euler totient function. Replacing each indeterminate zi in C(Cr, Zr) by
is the Euler totient function. Replacing each indeterminate zi in C(Cr, Zr) by
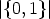 , which is equal to 2, we compute the number of all Cr-orbits on
, which is equal to 2, we compute the number of all Cr-orbits on 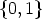 Zr
as
Zr
as
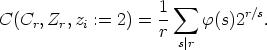
If we replace zi by 1 + zi, where z is an indeterminate over 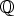 , then the number of C
r-orbits
of k-sets A
, then the number of C
r-orbits
of k-sets A 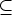 Zr is the coefficient of zk in
Zr is the coefficient of zk in
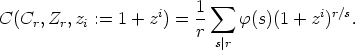
In conclusion (for the definition of 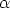 (r) see 6. in Lemma 4)
(r) see 6. in Lemma 4)
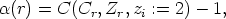
since we don’t count the orbit of the empty set. Similar methods can be applied to enumerate
the number of acyclic Cr-orbits on 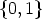 Zr or, what is equivalent to this, to enumerate all
Lyndon words of length r over the alphabet
Zr or, what is equivalent to this, to enumerate all
Lyndon words of length r over the alphabet 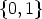 . For r > 1, this number is given as (for the
definition of
. For r > 1, this number is given as (for the
definition of 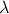 (r) see 8. in Lemma 4)
(r) see 8. in Lemma 4)
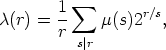
where 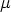 is the classical Moebius function. Moreover, the number of Lyndon words of length r
over
is the classical Moebius function. Moreover, the number of Lyndon words of length r
over 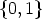 having r1 components 1 and r - r1 components 0 is
having r1 components 1 and r - r1 components 0 is
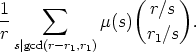
And the generating function of Lyndon words of length r over the alphabet 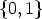 with r1
components 1 is of the form
with r1
components 1 is of the form
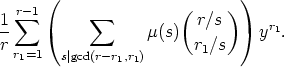
In the case r = 1 there are two Lyndon words, namely f0 = (0) and f1 = (1). The first one is
the characteristic function of the empty set in Z1 so we don’t want to count it. For that
reason, we must set  (1) = 1. Moreover, it should be mentioned that f0 is the unique Lyndon
word such that
(1) = 1. Moreover, it should be mentioned that f0 is the unique Lyndon
word such that  d(f0) is not a Lyndon word for d > 1.
d(f0) is not a Lyndon word for d > 1.
Finally, we have to combine all these results for enumerating the isomorphism classes of
canons. Let n > 1 be an integer. For any divisor d > 1 of n, let Mn,d be the set of all pairs
(L, Cn(A)), where L is a Lyndon word of length n over 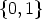 , (in the case n = 1 different
from 0) such that L(i) = 1 implies i
, (in the case n = 1 different
from 0) such that L(i) = 1 implies i  -1 mod d, and A is a non-empty subset of Zn, such
that d | k - l for all k, l
-1 mod d, and A is a non-empty subset of Zn, such
that d | k - l for all k, l  A. Hence
A. Hence
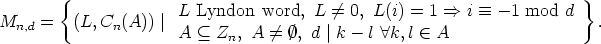
From Lemma 4 we deduce that  d describes a bijection between Mn,d and Mn/d,1,
thus
d describes a bijection between Mn,d and Mn/d,1,
thus
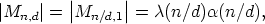
which is the number of possibilities to choose L and Cn(A) according to the desired
properties of Mn,d. Finally, let  n be the set of isomorphism classes of canons in
Zn,
n be the set of isomorphism classes of canons in
Zn,
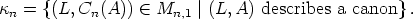
From Lemma 3 we deduce that
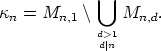
-
- Theorem. The number of isomorphism classes of canons in Zn is
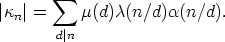
-
- Proof. First we prove that the set Mn,1 is the disjoint union
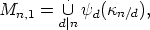
where
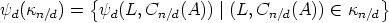
and
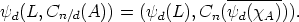
It is clear that Mn,1 contains this union. Moreover, this union is disjoint, since for a
canon K = (L, Cn/d(A)) 
 n/d we have
n/d we have
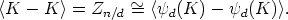
Finally, we have to show that each element of Mn,1 belongs to this union. If
(L, Cn(A))  Mn,1, then choose the biggest d such that (L, Cn(A)) belongs to Mn,d.
(I.e. (L, Cn(A)) does not belong to Mn,dd' for d' > 1. It is always possible to find
such d, since, if (L, Cn(A)) belongs both to Mn,d1 and Mn,d2, then it also belongs to
Mn,lcm(d1,d2).) Then there exists (L', C
n/d(A'))
Mn,1, then choose the biggest d such that (L, Cn(A)) belongs to Mn,d.
(I.e. (L, Cn(A)) does not belong to Mn,dd' for d' > 1. It is always possible to find
such d, since, if (L, Cn(A)) belongs both to Mn,d1 and Mn,d2, then it also belongs to
Mn,lcm(d1,d2).) Then there exists (L', C
n/d(A'))  M
n/d,1 such that L =
M
n/d,1 such that L =  d(L') and
d(L') and
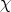 A0 =
A0 =  d(
d(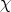 A0' ) for the canonical representatives A0 and A0' of C
n(A) and Cn/d(A').
Moreover, (L', C
n/d(A'))
A0' ) for the canonical representatives A0 and A0' of C
n(A) and Cn/d(A').
Moreover, (L', C
n/d(A')) 
 n/d because otherwise there would be some d' > 1 which is
a divisor of n/d such that (L', C
n/d(A'))
n/d because otherwise there would be some d' > 1 which is
a divisor of n/d such that (L', C
n/d(A'))  M
n/d,d' . But then (L, Cn(A)) also belongs to
Mn,dd' , which is a contradiction to the choice of d.
M
n/d,d' . But then (L, Cn(A)) also belongs to
Mn,dd' , which is a contradiction to the choice of d.
Hence,
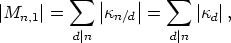
and by Moebius inversion we get
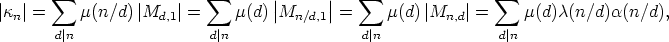
which finishes the proof. ![[]](lasy10-c-32.gif)
If 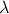 and
and 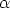 are replaced by the corresponding generating functions
are replaced by the corresponding generating functions
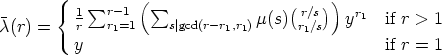
and
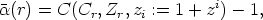
then the coefficient of yszt in
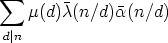
gives the number of non-isomorphic canons in Zn which consist of t voices where each voice
contains exactly s attack times.
For example the numbers of isomorphism classes of canons in Zn for 1 < n < 10
are:
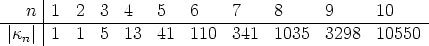
Finally, we have a closer look at the 13 isomorphism classes of canons in Z4, which
can be classified according to their number of voices and attack times per voice by
z4y3 + z4y2 + z4y + z3y3 + z3y2 + z3y + 2z2y3 + 2z2y2 + z2y + zy3 + zy2. From this list we
can read, for instance, that there are exactly three classes of canons with 4 voices
which have 1, 2, or 3 attack times per voice. Or we see that there are five classes of
canons with 2 voices, two of them having 3 attack times per voice, two of them
having 2 attack times per voice, and only one having 1 attack time in each of its two
voices.
We can even compute the canonical representative of each isomorphism class. For instance,
there are exactly three Lyndon words L1, L2, L3 of length 4 over 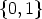 and five
representatives f1, ..., f5 of the C4-orbits of non empty subsets of Z4:
and five
representatives f1, ..., f5 of the C4-orbits of non empty subsets of Z4:

The Lyndon words describe the distribution of the attack times in one voice (i.e. the inner
rhythm of the canon), the necklaces describe the distribution of the voices over the complete
period, here in this example over Z4, which is the outer rhythm. Only L1 can be
constructed as  4((1)) or
4((1)) or  2((0, 1)) from shorter Lyndon words, so all pairs (Li, fj) for
i
2((0, 1)) from shorter Lyndon words, so all pairs (Li, fj) for
i 
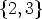 and j
and j 
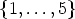 describe canons in Z4. Since f1 =
describe canons in Z4. Since f1 =  4((1)) =
4((1)) =  2((0, 1)) and
f3 =
2((0, 1)) and
f3 =  2((1, 1)), and (1), (0, 1), and (1, 1) are necklaces of length 1 or 2 over
2((1, 1)), and (1), (0, 1), and (1, 1) are necklaces of length 1 or 2 over 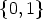 ,
the pairs (L1, C4(f1)) =
,
the pairs (L1, C4(f1)) =  4((1), C1(1)) and (L1, C4(f3)) =
4((1), C1(1)) and (L1, C4(f3)) =  2((0, 1), C2(1, 1)) do
not belong to
2((0, 1), C2(1, 1)) do
not belong to  4. But the pairs (L1, fj) for j
4. But the pairs (L1, fj) for j 
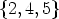 describe again canons in
Z4.
describe again canons in
Z4.
From this example we also see how to compute complete lists of isomorphism classes of
canons in Zn for arbitrary n. There exist fast algorithms for computing all Lyndon words and
all necklaces of length n over 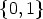 . Then each pair (Li, fj) must be tested whether there
exists some d > 1 such that (Li, fj) = (
. Then each pair (Li, fj) must be tested whether there
exists some d > 1 such that (Li, fj) = ( d(L'),
d(L'),  d(f')) for a Lyndon word L' and a necklace f'
of length n/d.
d(f')) for a Lyndon word L' and a necklace f'
of length n/d.
There exist more complicated definitions of canons. A pair (R, A) of inner and outer
rhythm defines a rhythmic tiling canon with voices V a for a  A in Zn if and only
if
A in Zn if and only
if
- the voices V a cover entirely the cyclic group Zn,
- the voices V a are pairwise disjoint.
It is obvious that periods and pulsations can be determined in cyclic time as well. Rhythmic
tiling canons with the additional property,
- the periods d(R) and d(A) coincide,
are called regular complementary canons of maximal category. So far we were not dealing with
that kind of canons.
Acknowledgment: The author wants to express his thanks to Guerino Mazzola for
pointing his attention to the problem of classification of canons. He is also grateful to Moreno
Andreatta, who provided very useful historic and background information about different
definitions of canons (cf [1]).
References
[1] M. Andreatta, Th. Noll, C. Agon, and G. Assayag. The geometrical groove: rhythmic
canons between theory, implementation and musical experiment. In Les Actes des
8e Journées d’Informatique Musicale, Bourges 7-9 juin 2001, pages 93-97, 2001.
[2] A. Kerber. Algebraic Combinatorics via Finite Group Actions.
B.I. Wissenschaftsverlag, Mannheim, Wien, Zürich, 1991. ISBN 3-411-14521-8.
[3] A. Kerber. Applied Finite Group Actions, volume 19 of Algorithms and
Combinatorics. Springer, Berlin, Heidelberg, New York, 1999. ISBN 3-540-65941-2.
[4] G. Mazzola. Topos of music. To appear.
[5] G. Pólya. Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und
chemische Verbindungen. Acta Mathematica, 68:145 - 254, 1937.
[6] G. Pólya and R.C. Read. Combinatorial Enumeration of Groups, Graphs and
Chemical Compounds. Springer Verlag, New York, Berlin, Heidelberg, London,
Paris, Tokyo, 1987. ISBN 0-387-96413-4 or ISBN 3-540-96413-4.
[7] D.T. Vuza. Supplementary sets and regular complementary unending canons (part
one). Perspectives of New Music, 29(2):22-49, 1991.
[8] D.T. Vuza. Supplementary sets and regular complementary unending canons (part
three). Perspectives of New Music, 30(2):102-125, 1992.
[9] D.T. Vuza. Supplementary sets and regular complementary unending canons (part
two). Perspectives of New Music, 30(1):184-207, 1992.
[10] D.T. Vuza. Supplementary sets and regular complementary unending canons (part
four). Perspectives of New Music, 31(1):270-305, 1993.
Harald Fripertinger
Institut für Mathematik
Karl Franzens Universität Graz
Heinrichstr. 36/4
A-8010 Graz, AUSTRIA
harald.fripertinger@uni-graz.at
|
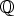 (marking the
attack times, or onsets) with R = R + d for a suitable period d. Furthermore, R is
supposed to be locally finite (i.e. the intersection of R with every time segment
[a, b] (of finite length b - a > 0) is finite). The period of a periodic rhythm R is the
smallest positive rational number d = d(R) satisfying R = R + d. We also mention
another important characteristic of a periodic rhythm, its pulsation p = p(R). It is
defined as the max
(marking the
attack times, or onsets) with R = R + d for a suitable period d. Furthermore, R is
supposed to be locally finite (i.e. the intersection of R with every time segment
[a, b] (of finite length b - a > 0) is finite). The period of a periodic rhythm R is the
smallest positive rational number d = d(R) satisfying R = R + d. We also mention
another important characteristic of a periodic rhythm, its pulsation p = p(R). It is
defined as the max 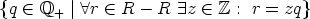 , in other words, it is
the biggest rational q such that all distances between the attack points of R are
integer multiples of q. Obviously, the period d is an integer multiple of the pulsation
p.
, in other words, it is
the biggest rational q such that all distances between the attack points of R are
integer multiples of q. Obviously, the period d is an integer multiple of the pulsation
p.
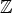
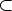
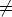
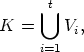

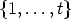
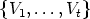 and
and
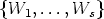 are called
are called 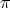


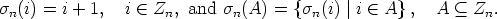
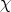

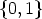 given
by
given
by
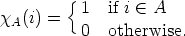
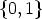
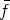 denote the subset
denote the subset  ) of
) of 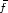 .
.
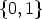 as vectors of
the form (
as vectors of
the form (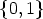
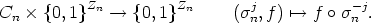
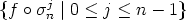 we choose the
function
we choose the
function 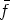
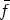 ) =
) =  . In general,
representatives of orbits
. In general,
representatives of orbits  0
0 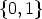
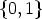
 ) is called
) is called 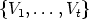 as a pair (
as a pair (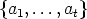 is a
is a 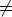 0
0 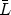
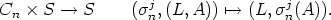
 0. This together with Lemma 2 proves
0. This together with Lemma 2 proves
 0
0 
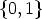

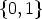 , such that
, such that 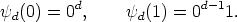
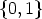
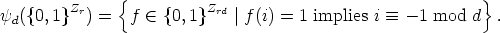
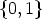
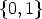
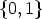
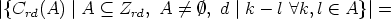
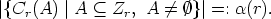
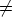 0
0 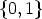
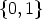
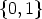
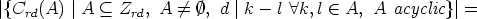
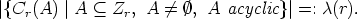
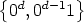 , the first statement is clear.
, the first statement is clear.
 . In other words,
. In other words, 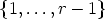 . Moreover, if
. Moreover, if 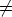 1, since
1, since ![[]](lasy10-c-32.gif)

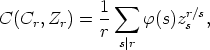
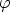
 , which is equal to 2, we compute the number of all
, which is equal to 2, we compute the number of all 
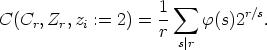
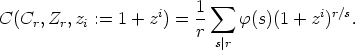
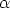
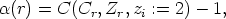
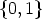
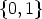 . For
. For 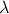
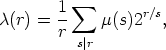
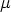
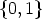 having
having 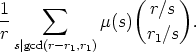
 with
with 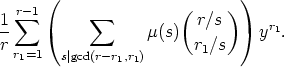
 , (in the case
, (in the case 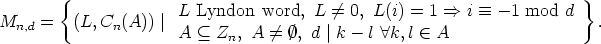
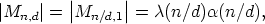

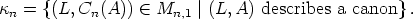
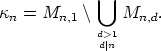
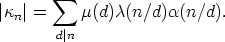
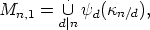
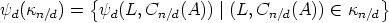
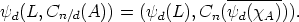
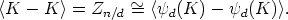
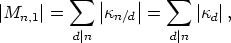
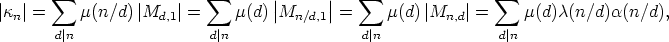
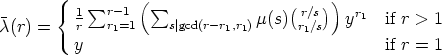
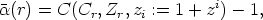
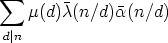
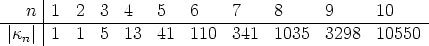
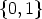 and five
representatives
and five
representatives 
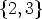 and
and 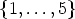 describe canons in
describe canons in 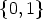 ,
the pairs (
,
the pairs (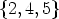 describe again canons in
describe again canons in
 . Then each pair (
. Then each pair (