| Symmetry adapted bases |
We discussed finite actions GX and their decomposition into orbits. The corresponding problem in linear representation theory is the decomposition of a representation space V, of D:G -> GL(V) say, into its irreducible constituents Vi:
V=V1Å...ÅVr.
This means that we have to find an adapted basis
{v1,...,vf1,vf1+1,...,vf1+f2,...},
where adapted means that {v1,...,vf1} is a basis of V1, while the following set {vf1+1,...,vf1+f2} is a basis of V2, and so on. In the case when we are given a complete set D1,...,Ds of pairwise inequivalent and irreducible matrix representations of G, we can do much better. If the irreducible subspace V1 affords an irreducible representation equivalent to Di, then we can find a basis {b1,...,bf1} that affords Di itself, which means, in formal terms, that the following holds, for each gÎG and 1£f1:
gbk:=D(g)bk=åj=1f1dijk(g)bj, if Di(g)= (dijk(g)).
A basis of V which has this property, is called a symmetry adapted basis of V with respect to the given system D1,...,Ds of irreducible matrix representations. Such a symmetry adapted basis has great advantages, since we know in advance, how each of the vectors vÎV transforms under the action of gÎG with respect to this particular basis. But the problem is that a complete system of ordinary irreducible matrix representations is available only in very few cases. Such a rare case is the symmetric group, as we have seen in the preceding section. Hence we would like to describe next, how a symmetry adapted basis can be evaluated for each representation space of the symmetric group Sn . (We restrict attention to the symmetric group, but the derivation of the symmetry adapted bases works in an analogous way for any other finite group G as well, as soon as we have the complete system of ordinary irreducible matrix representations at hand.)
Suppose we are given a complete system of ordinary irreducible matrix representations Da of Sn , and that V affords the representation D:Sn -> GL(V), a representation that is assumed to be reducible. We denote by m(a) the multiplicity of the irreducible representation [a] in D, and fa indicates the dimension of [a]. It is our aim to construct a basis
B:={baij | a|¾n,1£i£m(a),1£j£fa},
such that
D(p)baij=åk=1fadakj(p)baik.
Ordering this basis in a proper way:
B={...,ba11,...,ba1,fa, ba21, ...,ba2,fa, ...,bam(a),1, ...,bam(a),fa, ...},
the matrix corresponding to the (linear) action of pÎSn takes the
following form:
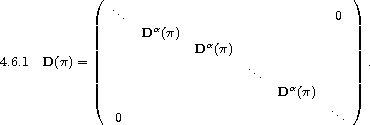 The square box containing the matrices Da (p) along its main diagonal
is called the homogeneous component of type a.
The square box containing the matrices Da (p) along its main diagonal
is called the homogeneous component of type a.
obvious from linear algebra. In order to construct such a basis from given tabulated matrix representations Da , i.e. from given numbers daik(p), for each pÎSn , 1£i,k£fa, we introduce the following linear operators on V:
Paji:=(fa)/(n!)åpÎSn daij(p-1)D(p).
Assume that the vectors ebkl,1£k£m(b),1£l£fb form asymmetry adapted basis. Then
Pajiebkl=(fa)/(n!)åp daij(p-1) D(p)ebkl
=faåm=1fa((1)/(n!)åp daij(p-1)dbml(p)) ebkm= dabdilbakj,
where the last equation is obtained from . This shows that the following is true, for any symmetry adapted basis of V:
Pajiebkl=eakj if a=b,i=l,
Pajiebkl= 0 otherwise.
This yields, for the product of two such operators:
PgrsPaji=dgadsjPari.
Another important consequence is
Corollary: The linear operator Paji introduced above is a projection operator that maps V onto the subspacePaji(V)=Waj:=<< eakj | 1£k£m(a) >> .
We are now in a position to construct a symmetry adapted basis. For this purpose we pick, for each a|¾n which is contained in D, any vector vÎV such that
ba1:=Pa11(v) not =0.
(Recall from the corollary above that the rank of Pa11 is nonzero if and only if [a] is contained in D.) Using this vector we put
baij:=Paji(ba1),
and we claim that these vectors form a symmetry adapted basis of V. In order to check this we use the last corollary which says that, for a fixed symmetry adapted bases {ebrs}, the vector baij, being an element of the image of Paji, is a linear combination of the following form:
baij=åk=1m(a)zkeakj.
Using this linear combination we obtain:
D(p)baij=åkD(p)eakj=åkzkål=1fa dalj(p)eakl=åldalj(p) åkzkeakl
=åldalj(p)Paljåkzkeakj=åldalj(p)Paljbaij=åldalj(p) PaljPaji(ba1),
which is, by the formula for the product of two such operators,
=åldalj(p)Pali(b1)=åldalj(p) baij,
as it is stated.
Some of the many interesting applications combine symmetry adapted bases with
eigenvalue considerations. For example, the natural representation of the
cyclic group Cn=á(1...n)ñ is generated by the matrix
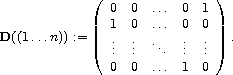 Its characteristic polynomial
Its characteristic polynomial
det(xI-D((1...n)))=xn-1
shows that the eigenvalues are exactly the powers of a primitive n-th root of unity w:=e2pi/n:
wj:=wj=e2pij/n.
This implies that the homogeneous components are onedimensional (which means that the irreducible constituents of the natural representation of the cyclic group are pairwise different, this representation is in fact a model for the cyclic group). A symmetry adapted basis therefore consists of eigenvectors corresponding to pairwise different eigenvalues, and so the arguments used in the proof imply the following:
Corollary: Each matrix that commutes with D((1...n)) becomes diagonal if we change the basis into a symmetry adapted one. Hence in particular the eigenvectors of D((1...n)) are eigenvectors of the commuting matrix, too.
A nice application is the following derivation of Cardano's formula for the solutions of cubic equations:
Example: The following matrix clearly commutes with D((123)):The characteristic polynomial of this matrix is
x3-3abx-a3-b3.In order to derive its roots we can use corollary. Putting w:=e2pi/3, we obtain fromthis corollary the following eigenvectors of M:Hence the eigenvalues of the matrix M turn out to be
l1=a+b,l2=aw2+bw,l3=aw+bw2.We can apply this now to a cubic equation of the formx3+px+q=0,obtaining p=-3ab,q=-(a3+b3), from which we derive Cardano's formulae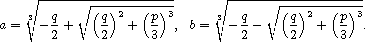
A more important application of symmetry adapted bases is the evaluation of the irreducible polynomial representations áañ of the general linear group GLm(Q), which arise by symmetrizing the identity map:
áañ:=id[a],
but the details of this form quite a long story, and so I refer to the corresponding literature (see the chapter with comments and references).
| harald.fripertinger "at" uni-graz.at | http://www-ang.kfunigraz.ac.at/~fripert/ | UNI-Graz | Institut für Mathematik | UNI-Bayreuth | Lehrstuhl II für Mathematik |
| Symmetry adapted bases |