| Transversals of symmetry classes |
In this section we shall restrict attention to a redundancy free construction
of a transversal of the G-classes on YX:=mn. Moreover, in order to
decrease the complexity we restrict attention to G-classes of fixed content
l=(l1,...) n, starting off from the canonic
mapping f with this content:
n, starting off from the canonic
mapping f with this content:
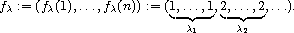 The set of all the mappings of this content will be indicated as follows:
The set of all the mappings of this content will be indicated as follows:
mnl :={pfl=fl o p-1 | pÎSn }.
Since a permutation of the arguments does not change the content, this set mnl is a union of orbits of G on mn :
G\\mnl ÍG\\mn .
We would like to construct a transversal of mnl . This reduces the complexity
since the desired transversal of G\\mn is the union of the transversals
of the sets G\\mnl , taken over all the l n.
The crucial point is
now that in each orbit of G on mnl
there is a unique representative which is the lexicographically
smallest element of its orbit. Therefore we may call these lexicographically
smallest elements a canonic transversal of G\\mnl .
A mapping fÎmnl can be displayed by its
l-tabloid
n.
The crucial point is
now that in each orbit of G on mnl
there is a unique representative which is the lexicographically
smallest element of its orbit. Therefore we may call these lexicographically
smallest elements a canonic transversal of G\\mnl .
A mapping fÎmnl can be displayed by its
l-tabloid
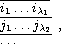 where we put the elements of the inverse image f-1[{k}] of
kÎm into the
k-th row, in increasing order, so that e.g.
where we put the elements of the inverse image f-1[{k}] of
kÎm into the
k-th row, in increasing order, so that e.g.
f(i1)=...=f(il1)=1, and i1<...<il1.
Let us consider as an example the graphs on 4 vertices which contain exactly 2 edges, so that n= 4 choose 2=6, m=2, and l=(4,2). Before we write down all the 15 (4,2)-tabloids in full detail, it is practical to note that in each tabloid the first (or any other) row is uniquely determined by the remaining rows which form the truncated tabloid. Hence in the present case we need only to display the second rows, here they are:
bar (12), bar (13), bar (14), bar (15), bar (16), bar (23), bar (24), bar (25), bar (26), bar (34), bar (35), bar (36), bar (45), bar (46), bar (56).
According to the above arguments we have to find the orbits of bar (S4) on this set. Recall that the elements 1,...,6Î6 on which S6 acts, stand for the pairs {1,2},...,{5,6} of vertices. The subgroup
bar (S4):=S4[2] hookrightarrow S6
is the permutation group induced by S4=á(12),(1234) ñ on this set of pairs of vertices. Thus
bar (S4)=á(24)(35),(1463)(25)ñ,
and therefore one of the two orbits of bar (S4) on the set of (4,2)-tabloids is
w2:={bar (16),bar (25),bar (34)},
the other orbit w1 consists of the remaining 12 truncated tabloids. (Note that in a preprocessing calculation we can obtain, by an application of the enumeration theory described above, that the number of graphs with 4 vertices and 2 edges is two, a result which is very helpful as stopping rule, as the present example already shows!)
The lexicographically smallest elements of these orbits w1,w2
are the tabloids corresponding to
bar (56)Îw1 and
bar (34)Îw2. These tabloids are
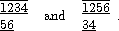 The corresponding mappings f,f'Î26 are
The corresponding mappings f,f'Î26 are
f=(1,1,1,1,2,2), and f'=(1,1,2,2,1,1).
Hence the graphs shown below form a
complete set of graphs on 4 vertices containing 2 edges!
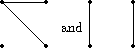
This method is cumbersome, it can be used for cataloging the graphs on £7 vertices, say. We want therefore to describe further refinements which allow to catalog the graphs with v=10 vertices (this is in fact the biggest v for which a complete such list is available, there are approximately 12·106 such graphs).
Having displayed an example in full, let us go into detail in order to make the procedure of finding the minimal representatives more efficient. Recall that we have to check if a given f is the lexicographically smallest element in its orbit, i.e. if the following is true:
" sÎbar (G):f£f o s, for short: f£bar (G)(f).
The verification of this condition is one of the crucial parts of the whole procedure. Let us call this check the minimality test for f. In order to carry it out in a reasonable way we recall what has been said about Sims chains. Assume that b is the base for the action of bar (G) on n (still fÎmn ), so that
{1}=Cbar (G)(b )£Cbar (G)(b-1)£...£Cbar (G)(0)=bar (G),
and we assume that left coset representatives pj(i) ar at hand such that
Cbar (G)(i-1)=Èj=1r(i)pj(i) Cbar (G)(i), where p1(i)ÎCbar (G)(i).
Thus, in order to apply the minimality test, we have to run through the elements of bar (G), each of which can uniquely be written in the form
s=pj1(1)...pjb(b).
This means that in order to apply each element of bar (G) to f, say, we have to run through the following tree:
It is very important to cut this tree down as much as possible. This can be done, for example, by an application of
Lemma: If f<f o pj(i) and f(i)<f o pj(i)(i), then we have, for the orbit of f under the action of Cbar (G)(i) £bar (G):f<Cbar (G)(i)(f o pj(i)).
Proof: For tÎCbar (G)(i) and kÎi-1 we have
f o pj(i) o t-1(k)=f(k),
while
f o pj(i) o t-1(i)= f o pj(i)(i)>f(i).
This result allows us to cut off the branch starting with the element ...pj(i) from the tree formed by the elements of bar (G).
Besides this we can choose a suitable way in which we work through the tree in order to find the smallest element in the orbit G(f). A remark that will lead us to a good such choice makes use of the fact that fÎmn will not in general be injective. But in this case there exist t,sÎSn \{1} such that f o s=f o t, and so we have for each iÎn the equation
s-1Cbar (G)(i)(f)= t-1Cbar (G)(i)(f).
We can therefore subdivide bar (G) according to the Sims chain and the base b :
bar (G)=Èi=1b(Cbar (G)(b-i)\Cbar (G) (b-i+1))È{1}.
Correspondingly we shall run through bar (G) (in any case, whether f is injective or not) by working through the following subsets, one row after the other, from top to bottom:
The identity element can be left out since f o 1= f. We note that in step number b-i+1 we are running through the set
Cbar (G)(i-1)\Cbar (G)(i) =Èj=2r(i)pj(i)Cbar (G)(i),
if we had f£Cbar (G)(i) (f) before, assuming that p1(i)=1, for each i, so that we can always start with j=2. This way to procede allows to use the following remark: In the case when there exists any sÎCbar (G) (i) for which f o pj(i) o s= f, then pj(i)Cbar (G)(i)(f)³f, and so we can jump over the whole coset pj(i)Cbar (G) (i), by the formula. This idea can also be used in order to derive the Sims chain of the stabilizer of f. Let us indicate this stabilizer as follows:
A:={rÎbar (G) | f o r=f} £bar (G),
and note that, for each iÎb :
CA(i)£Cbar (G)(i).
A transversal of the set of left cosets CA(i-1)/CA(i) can be obtained from the transversal {pj(i) | jÎr(i)} of Cbar (G)(i-1)/Cbar (G)(i) in the following way:
Lemma: If we denote by J(i) the setJ(i):={jÎr(i) | $sjÎCbar (G)(i) :pj(i)sjÎA},and if we fix, for each jÎJ(i), such an element sj, then{tj:=pj(i)sj | jÎJ(i)}is a transversal of CA(i-1)/CA(i).
Proof: If sÎCA(i), then, by the formula, there exists a jÎr(i) such that sÎpj(i)Cbar (G) (i), so that this j must lie in J(i). Moreover the left cosets tjCA(i) are pairwise different, since the formula holds.
Corollary: The set{tj=pj(i)sj | jÎJ(i)}yields the Sims chain of the stabilizer A of f.
Another byproduct is the following test:
Corollary: If, for each i,j, f'(i) not =f o pj(i)(i), thenf' not ÎG(f).
Let us now summarize what has been said so far about the minimality test which we have to carry out in order to find the lexicographically smallest element of the orbit G(f). We discussed the Sims chain for the action of G on n, it leads to the tree, and we saw in the lemma that certain cuts and jumps can be made while running through this tree. But still this does not suffice to carry out this test in an efficient way, say if we want to catalog the graphs on 10 vertices. We shall therefore continue by considering the evaluation of the orbits of the centralizers Cbar (G)(i).
| harald.fripertinger "at" uni-graz.at | http://www-ang.kfunigraz.ac.at/~fripert/ | UNI-Graz | Institut für Mathematik | UNI-Bayreuth | Lehrstuhl II für Mathematik |
| Transversals of symmetry classes |