Sn as a Coxeter Group

Sn as a Coxeter Group

Reduced decompositions play a role also in the theory of other groups. The symmetric group S_n is in fact a Coxeter group,  

which means that there exists a set of generators s_i such that the relations are of the particular form (s_is_j)^m_ij=1, where

m_ij ÎN, m_ii=1, m_ij=m_ji>1, if i not =j.

In the case of the symmetric group S_n , the Coxeter system of generators is the subset S _n of elementary transpositions s_i=(i,i+1), as we have seen already. Furthermore, this leads us to introduce the weak Bruhat order  

p ·r : Û l( r)=l( p)+1, and $ s_i :r= ps_i.

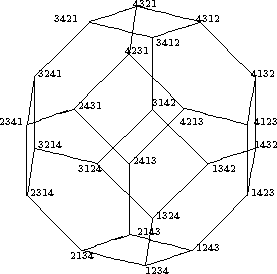
The Bruhat order of the symmetric group S ₄ is shown in figure. We note that the number of reduced decompositions (and also the set of reduced decompositions) can be obtained by going from the identity upwards in all the possible ways until the permutation in question is reached.  

We are now approaching a famous result on reduced sequences for the proof of which we need a better knowledge of the set of inversions. In order to describe how I( ps_i), s_i ÎS _n, arises from I( p), we use that S_n acts on n² in a canonic way: r(i,j)= ( ri, rj). Keeping this in mind, we easily obtain:

I( ps_i)= s_iI( p) È{(i,i+1) } if pi< p(i+1)

and

I( ps_i)= s_iI( p) \{(i,i+1) } if pi> p(i+1).

This yields for the corresponding reduced lengths:

l( ps_i)= l( p)+1 if pi< p(i+1)

and

l( ps_i)= l( p)-1 if pi> p(i+1),

in accordance with the Lemma. If w_n denotes the permutation [n, ...,1] of maximal length, then

l( w_n)=[n choose 2], l( w_n r)=[n choose 2]-l( r)=l( rw_n).

Proof: Clearly I( w_n)= {(i,j) În² | i<j }, and hence l( w_n)=[n choose 2]. Moreover

rw_n=[ rn, ..., r1],

so I( rw_n)= n² \I( r), and l( rw_n)=[n choose 2]- l( r). Finally we note that

l( w_n r)=l(( w_n r)^-1)=l( r^-1 w_n) =[n choose 2]-l( r^-1)=[n choose 2]-l( r),

which completes the proof.

An expression

p= s_i1...s_il, s_i ÎS _n,

of p in terms of elementary transpositions and minimal l=l( p) was called a reduced decomposition of p. The set of corresponding sequences of indices is indicated as follows:

RS( p):= { (i₁,...,i_l) | p= s_i1...s_il, s_i ÎS_n,l minimal }.

These sequences are called reduced sequences  

of p.

Sn as a Coxeter Group