Reinhard Laue, Alfred Wassermann,
University of Bayreuth, Germany
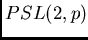
on 6-element subsets of the projective line with
prescribed non-trivial stabilizer are described. A refinement of cross-ratio
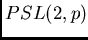
computations to orbits allows to determine the orbits on
5-element subsets that they cover. Then Steiner 
-
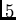
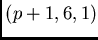
designs
are assembled from them. In particular, there is one isomorphism type
of -
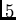
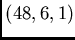
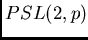
designs that consists of orbits of the same size,
each being a 
-
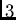
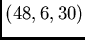
design. There are 7 isomorphism types
of -
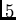
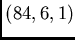
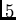
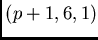
designs of this type. Generally, Steiner - designs
with such an orbit partition may only exist if
.
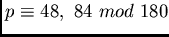